湖南省攸县二中2019届高三上学期期中考试（第四次月考）数学（理）试卷

湖南省攸县二中2019届高三上学期期中考试（第四次月考）数学（理）试卷

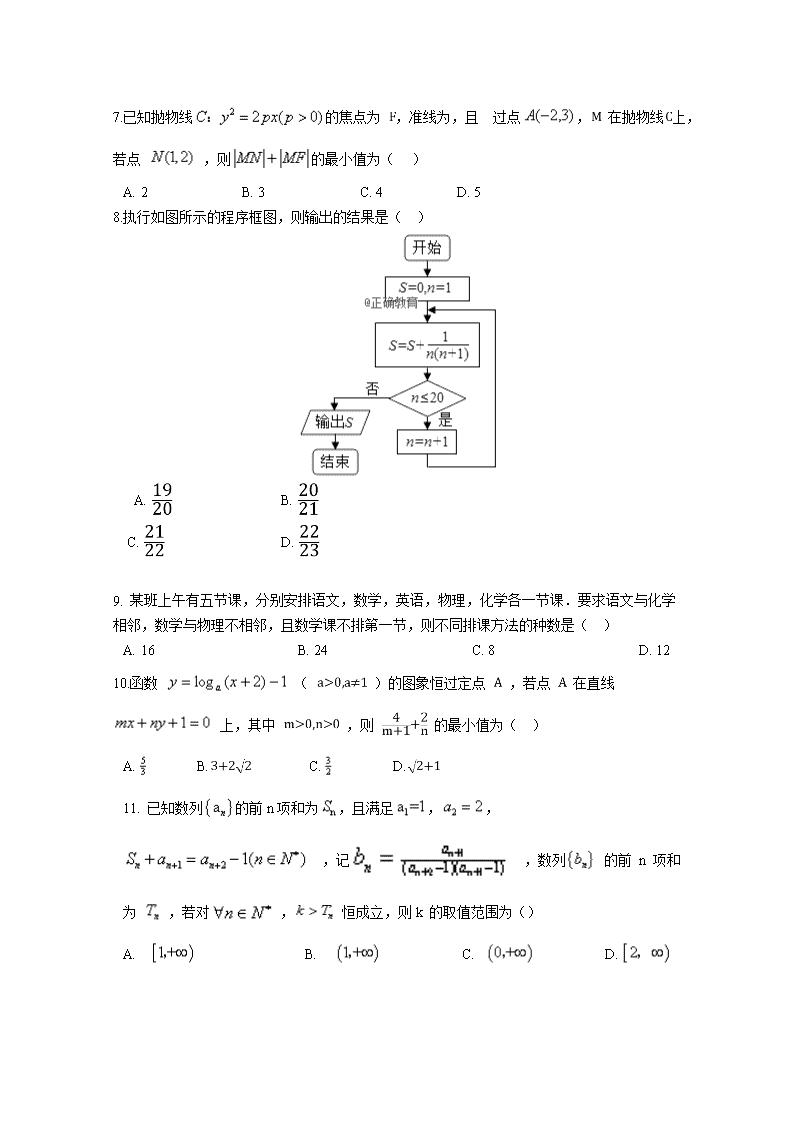
攸县二中2019届高三第四次月考试题 数学（理科）11月 考试时量：120分钟；总分：150分 注意事项：‎ ‎1．请在答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 一、选择题（本大题共12小题，每小题5分，共60分，每小题仅有一个答案是正确的）‎ ‎1.已知全集， 集合， ， 则（     ） ‎ A.        B.                         C.                             D. ‎ ‎2.已知（ 为虚数单位) ，则复数 的虚部为（   ） ‎ A.                                           B. 1                                          C.                                           D. 2‎ ‎3．下列命题中正确的是（）‎ A．若p∨q为真命题，则p∧q为真命题 B．“a＞0，b＞0”是“”的充要条件 C．命题“x2﹣3x+2=0，则x=1或x=2”的逆否命题为“若x≠1或x≠2，则x2﹣3x+2≠0”‎ D．命题p：，使得x2+x﹣1＜0，则￢p：，使得x2+x﹣1≥0‎ ‎4.已知F1， F2是双曲线E： 的左、右焦点，点M在E上，MF1与x轴垂直，‎ 且sin∠MF2F1= ，则E的离心率为（   ） ‎ A.                                          B.                                         ‎ ‎ C.                                          D. 2‎ ‎5.设等差数列的前 项和为，且， ，则满足 的最大自然数 为（   ） ‎ A. 12                                         B. 13                                         C. 22                                         D. 23‎ ‎6.函数（其中e为自然对数的底数）图象的大致形状是（    ） ‎X Y A X y B X y C X y D X Y A X y B X y C X y D ‎7.已知抛物线的焦点为 ，准线为，且 过点， 在抛物线上，若点 ，则的最小值为（    ） ‎ A. 2                           B. 3                           C. 4                     D. 5‎ ‎8.执行如图所示的程序框图，则输出的结果是（   ）‎ ‎ A.                              B.                                        ‎ C.         D. ‎ 9. 某班上午有五节课，分别安排语文，数学，英语，物理，化学各一节课．要求语文与化学相邻，数学与物理不相邻，且数学课不排第一节，则不同排课方法的种数是（   ） ‎ A. 16                                         B. 24                                         C. 8                                         D. 12‎ ‎10.函数 （ ）的图象恒过定点 ，若点 在直线 上，其中 ，则 的最小值为（   ） ‎ A. B. C. D.‎ ‎11. 已知数列的前n项和为，且满足，， ，记 ，数列 的前 n 项和为 ，若对 ， 恒成立，则k 的取值范围为（）‎ A.                                   B.                            C.                       D. ‎ ‎12.已知四面体 AB CD 的外接球球心O恰好在棱AD上，且 ， ，，则这个四面体的体积为（     ） ‎ A.                          B.                             C.                              D. ‎ 二、填空题（本大题共4个小题，每小题5分，共20分）‎ ‎13.若 满足不等式 , 则 的最大值为________. ‎ ‎14.已知向量与的夹角为 ， ， ，则 ________. ‎ ‎15.已知函数，，若存在常数，对，唯一的，使得，则称常数是函数在上的“几何平均数”.‎ 已知函数，，则在上的“几何平均数”是．‎ 16. 已知函数，函数 ‎ 有三个零点，则实数 的取值范围为________． ‎ 三、解答题（本大题共6小题，共70分，解答题需要写出必要的解答过程）‎ ‎17.（本小题满分12分）‎ 设的内角 的对边分别为a,b,c 且 . ‎ ‎（1）求角 B 的大小; ‎ ‎（2）若， , 求边 a和 c 的值. ‎ ‎18.（本小题满分12分）‎ 某数学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，结果如下表：记成绩不低于70分者为“成绩优良”．‎ 分数 ‎[50,59)‎ ‎[60,69)‎ ‎[70,79)‎ ‎[80,89)‎ ‎[90,100]‎ 甲班频数 ‎5‎ ‎6‎ ‎4‎ ‎4‎ ‎1‎ 乙班频数 ‎1‎ ‎3‎ ‎6‎ ‎5‎ ‎5‎ ‎（1）由以上统计数据填写下面2×2列联表，并判断“成绩优良与教学方式是否有关”?‎ 甲班 乙班 总计 成绩优良 成绩不优良 总计 ‎（2）甲乙两班成绩未达优良的同学共15位，老师现从中任意抽取3人进行谈话，以便了解学习情况．在这3人中，记乙班成绩不优良的人数为 ，求 的分布列及数学期望． 附：   ．      临界值表如下： ‎ ‎ 0.010‎ ‎19.（本小题满分12分）‎ 如图，在四棱锥 中，底面 为平行四边形， ， ，‎ 且 .‎ ‎（1）证明： ； ‎ ‎（2）若 为 的中点，且 ，求二面角 的大小. ‎ ‎20 . （本小题满分12分）‎ 已知椭圆 : (), 过点，离心率为 . （Ⅰ）求椭圆 的方程； （Ⅱ） ， 是过点 且互相垂直的两条直线，其中 交圆 于 ， 两点， 交椭圆 于另一个点 ，求面积取得最大值时直线 的方程. ‎ ‎21. （本小题满分12分）‎ 已知函数，曲线在x = 1处的切线方程为。 ‎ ‎（1）求a和b的值； ‎ ‎（2）求函数在上的最大值； ‎ ‎（3）证明：当x > 0时，. ‎ ‎22.（本小题满分10分）‎ 在直角坐标系中，曲线 的参数方程为 （ 为参数）.在以坐标原点为极点，轴正半轴为极轴的极坐标系中，直线 的极坐标方程为 ，其中 . （Ⅰ）求 的极坐标方程； （Ⅱ）若 与 交于不同两点A和B ，且 ，求 的最大值. ‎ 攸县二中2019届高三第四次月考 数学（理科）参考答案 一、单选题(每小题5分，共60分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C D D A C B B C A B A D ‎11.【答案】A ‎【解答】由 ，得 ，两式作差得 又 ， ，可求得a3=4,所以数列 是等比数列，且 ，代入   ，所以 而 恒成立，所以 ，故选A 【分析】,得到两式子一减得到,进而求出的通项，将其通项代入,裂项得到，求其前n项和可以采用裂项相消法，最后便可以计算出k的范围。‎ ‎12.【答案】D ‎【解答】∵ ，AC=2， ∴AB2+BC2=AC2 ， ∴AB⊥BC ， ∴△ABC外接圆的直径为AC,圆心O′为AC的中点 ∵球心O恰好在侧棱DA上, ∴ ，又外接球球心O恰好在棱AD上，所以O为AD中点，所以//BC. 即 ， ， 四面体的体积为 . 故答案为：D. 【分析】由数据得到AB⊥BC,则直角△ABC外接圆的直径为AC,圆心O′为AC的中点,‎ 得到DC ⊥面A B C ,再由体积公式求体积.‎ 二、填空题(每小题5分，共20分）‎ ‎13.【答案】14.【答案】6 ‎ ‎15.【答案】16.【答案】‎ ‎16.【解答】由题得 有三个零点， 所以 有三个零点，‎ ‎ 所以函数h(x)的图像就是坐标系中的粗线部分， y=a(x-2)表示过定点（2,0）的直线，所以直线和粗线有三个交点. 所以 由题得, . 所以, 所以a的取值范围为 . 【分析】本题的突破口是研研究结构特征，从而将g(x)=0的零点问题转化为,于是可以通过作图加以研究解决。‎ 三、解答题（本大题共6小题，共70分)‎ ‎17.【解答】（1）解:bsinA= acosB,由正弦定理可得 .................2分 即得>0.....................................................................................................................4分 ‎ ,................................................................................5分 ..........................................................................................................................................6分.. （2）解:sinC=2sinA,由正弦定理得c=2a,...............................................................................8分 由余弦定理 , ‎ ‎, 解得...............................................................................10分 ................................................................................12分 ‎【分析】（1）利用正弦定理边化角，得B角的正切，求得B. （2）利用正弦定理角化边，再用余弦定理解得a和c.‎ ‎18.【解答】（1）解：根据题意得2×2列联表如下：‎ 甲班 乙班 总计 成绩优良 ‎9‎ ‎16‎ ‎25‎ 成绩不优良 ‎11‎ ‎4‎ ‎15‎ 总计 ‎20‎ ‎20‎ ‎40‎ ‎ ..........................2分 根据2×2列联表中的数据，得 的观测值为 ‎ ，.......................................................4分 在犯错概率不超过0.05的前提下认为“成绩优良与教学方式有关”.............6分 9. 由题可知 的可能取值为0,1,2,3．.......................................................................7分 ； ； ；．‎ 的分布列为：‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎..............................................10分 所以...............................................12分 ‎ 【分析】（1）将列联表填写完整，结合K2的计算公式，计算结果，即可得出答案。‎ ‎（2）分别计算出X=0，1，2，3的概率，列出分布列，计算期望，即可得出答案。‎ 16. ‎【解答】（1）证明：∵ ，‎ ‎∴ ，‎ ‎ ，‎ ‎∴ ........................................................1分 又∵ 底面 ，‎ ‎∴ ........................................................2分 ∵ ，‎ ‎∴ 平面 .............................................3分 平面 ，.......................................4分 ‎∴平面 平面 ...................................5分 ‎ ‎（2）解：由（1）知，DA,DB,DP两两垂直 ，分别以 ， ， 为 轴， 轴，轴建立空间直角坐标系 ，‎ 如图所示，设AD=1得AB=2, ，令 ，‎ 则 ， ， ， ， ，...............6分 ‎∴ . ∴ ，∴ .....................................................................7分 故 ， .................................................8分 设平面 的法向量为 ， 则， 令 ，得，即 ..........................................................9分 易知平面 的一个法向量为 ，........................................10分 则 .............................................................11分 ‎ ∴二面角 的大小为 . ............................................................12分 ‎【分析】（1）根据勾股定理得出BC⊥BD，结合PD⊥BC可得BC⊥平面PBD，利用平面与平面垂直的判定得出平面PBD⊥平面PBC； （2）建立坐标系，求出平面QBD和平面BCD的法向量，用空间向量求平面间的夹角，得出二面角的大小．‎ ‎（注：由于命题出现失误，此题第2问存在问题，应该没有固定结果，为使评价近似合理，建议阅卷作如下标准记分：学生采用“设AD=1”方法所得出参考答案中结果的记满分，学生采用设其他具体数据算出余弦值或角度的记满分，如果学生考虑周密认为只能设AD为字母参数而算不出结果也得满分。命题组给大家带来麻烦还敬请谅解）‎ 16. ‎【解答】解：（1）由题意得.........................................2分 解得........................................4分 所以椭圆方程为.........................5分 方法二：由得....................................1分 .....................................................................................2分 由椭圆经过点P（0，2））得...................................3分 所以......................................................................................4分 所以椭圆方程为..................................................5分 ‎（2）由题知直线 的斜率存在，不妨设为 ，则 ： . ........................6分 若 时，直线 的方程为 ， 的方程为 ，易求得 ， ，此时 . .......................................7分 若 时，则直线 ： . 圆心 到直线 的距离为 . 直线 被圆 截得的弦长为 ‎ . ......................................8分 .由   ， 得 ， ‎ 故   . ......................................9分 所以       . ......................................10分 当 时上式等号成立. .....................................11分 因为 ， 所以 面积取得最大值时直线 的方程应该是.....................................12分 ‎【分析】（1）结合椭圆的基本性质列方程，即可得出答案。（2）分k=0和k不为0两种情况讨论，结合直线l1的方程和圆方程，用k表示|AB|的长，结合直线l2和椭圆方程，利用所截的弦长为,表示线段PD，结合三角形面积计算公式，即可得出答案。‎ ‎21 【解答】解：（1），.................................1分 由题设得，，，...........2分 ‎ 解得，． ................................3分 ‎ （2） 法1：由（1）知，，.........4分 因为当时，所以当时，‎ ‎，‎ 故在上单调递增，.................................5分 ‎ 所以．................................6分 ‎ 法2：由（1）知，，.........4分 ‎ 在上单调递减，在上单调递增， ‎ 所以， ‎ 所以在上单调递增，...........................5分 ‎ 所以，． ...........................6分 ‎ （2） 因为，又由（2）知，过点，‎ 且在处的切线方程为，‎ 故可猜测：当时，的图象恒在切线的上方．........7分 ‎ 下证：当时，． ‎ 设，则，‎ 由（2）知，在上单调递减，在上单调递增， ‎ 又，‎ 所以存在，使得 ‎ 所以当时，；当，， ‎ 故在上单调递增，在上单调递减，在上单调递增． ‎ 又（当且仅当时取等号） ‎ 故.............................10分 ‎ 因为当时，故当时，‎ 当且仅当时取等号， 所以当时． ‎ 即，所以， ‎ 即成立（当时等号成立）． ……12分 ‎ ‎22【答案】解：（Ⅰ）消去参数 得到 的普通方程为..........................2分 再将， 代入 的普通方程中，得到 的极坐标方程为 ．.....................................................................4分 （Ⅱ）将 代入 ，‎ 得 .....................................................................6分 令 ，得 ， 已知 ，解得    ......................................................................7分 ‎ 设 ，则 ‎， 则 ............................................8分 所以......................9分 又 ，所以当 即 时 的最大值为 ．...............................................10分 ‎ ‎【解析】（1）将参数方程化成普通方程，再利用代入，化简，即可得出答案;‎ ‎（2）把题目所求的式子转化成三角函数的形式，再求三角表达式的最大值，即可得出答案。‎