数学文卷·2018届广西桂林市第十八中学高二上学期段考（期中）（2016-11）

数学文卷·2018届广西桂林市第十八中学高二上学期段考（期中）（2016-11）

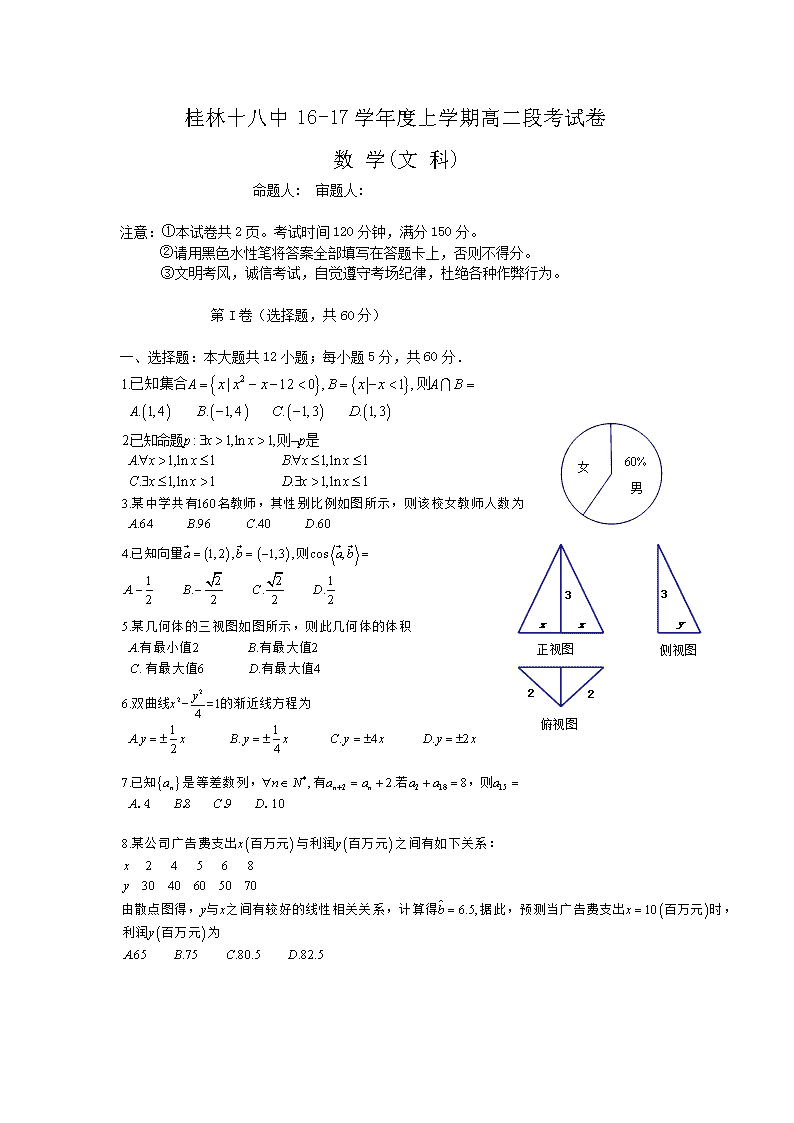
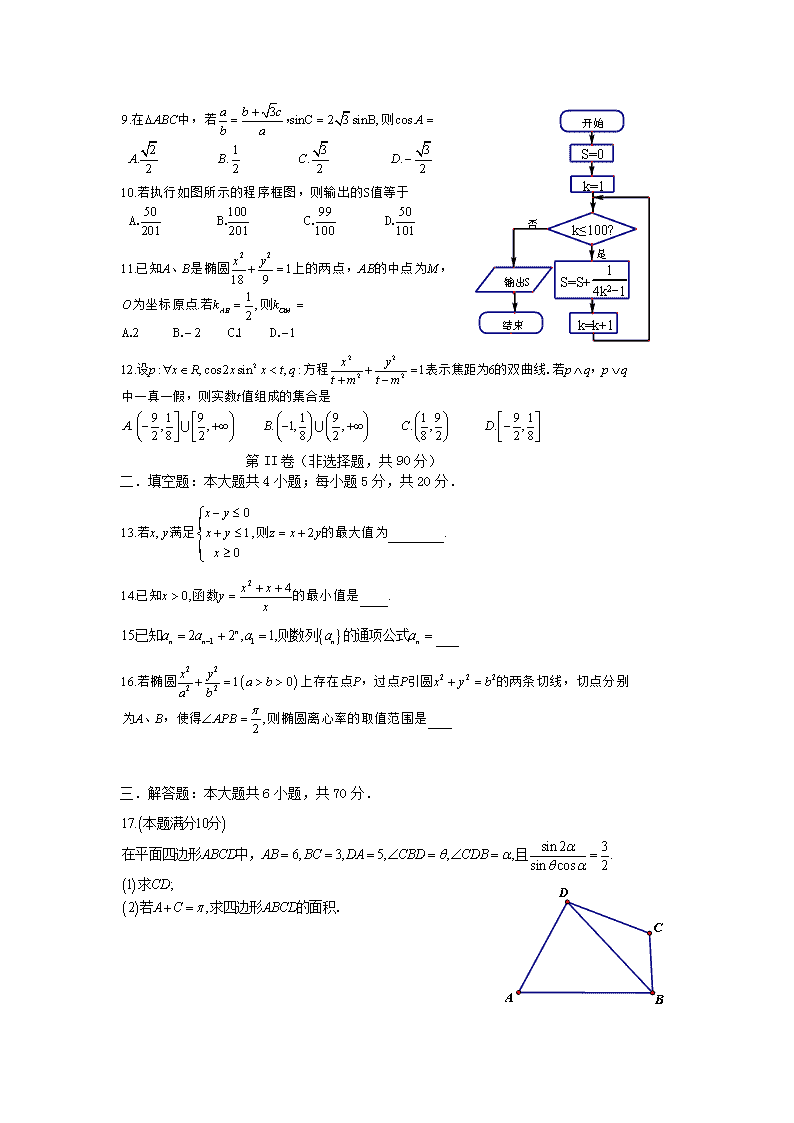
桂林十八中16-17学年度上学期高二段考试卷 数 学(文 科)‎ 命题人: 审题人: ‎ 注意：①本试卷共2页。考试时间120分钟，满分150分。‎ ②请用黑色水性笔将答案全部填写在答题卡上，否则不得分。‎ ③文明考风，诚信考试，自觉遵守考场纪律，杜绝各种作弊行为。‎ 第I卷（选择题，共60分）‎ 一、选择题：本大题共12小题；每小题5分，共60分．‎ 第II卷（非选择题，共90分）‎ 二．填空题：本大题共4小题；每小题5分，共20分．‎ 三．解答题：本大题共6小题，共70分．‎ 如图，四棱锥P—ABCD中，底面ABCD为矩形，PA⊥面ABCD，E为PD的中点. ‎ ‎(1)证明：PB//平面AEC;‎ ‎(2) 若AP=1，AD=,，求A到平面PBC的距离.‎ 桂林十八中16-17学年度上学期高二段考试卷数 学文科参考答案一.选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B A A C B D C D C B D A 二.填空题 ‎ ‎ 三．解答题 ‎(2)解　由A＋C＝，得C＝－A，‎ 在△ABD中，有BD2＝AB2＋AD2－2AB·ADcos A，‎ 在△BCD中，有BD2＝BC2＋CD2－2BC·CDcos C，‎ 所以AB2＋AD2－2AB·ADcos A＝BC2＋CD2＋2BC·CDcos A，‎ 则cos A ＝ ‎＝＝，‎ 于是sin A＝＝ ＝.‎ ‎19.解：（I）连接BD交AC于点O,连结EO。‎ ‎ 因为ABCD为矩形，所以O为BD的中点。‎ 又E为PD的中点，所以EO∥PB。‎ ‎ EO平面AEC,PB平面AEC,‎ 所以PB∥平面AEC.‎ ‎(2)作 由题设知平面PAB,所以 故又,‎ 所以A到平面PBC的距离为.‎