2017-2018学年广西南宁市第三中学高二下学期第三次月考数学（理）试题 Word版

2017-2018学年广西南宁市第三中学高二下学期第三次月考数学（理）试题 Word版

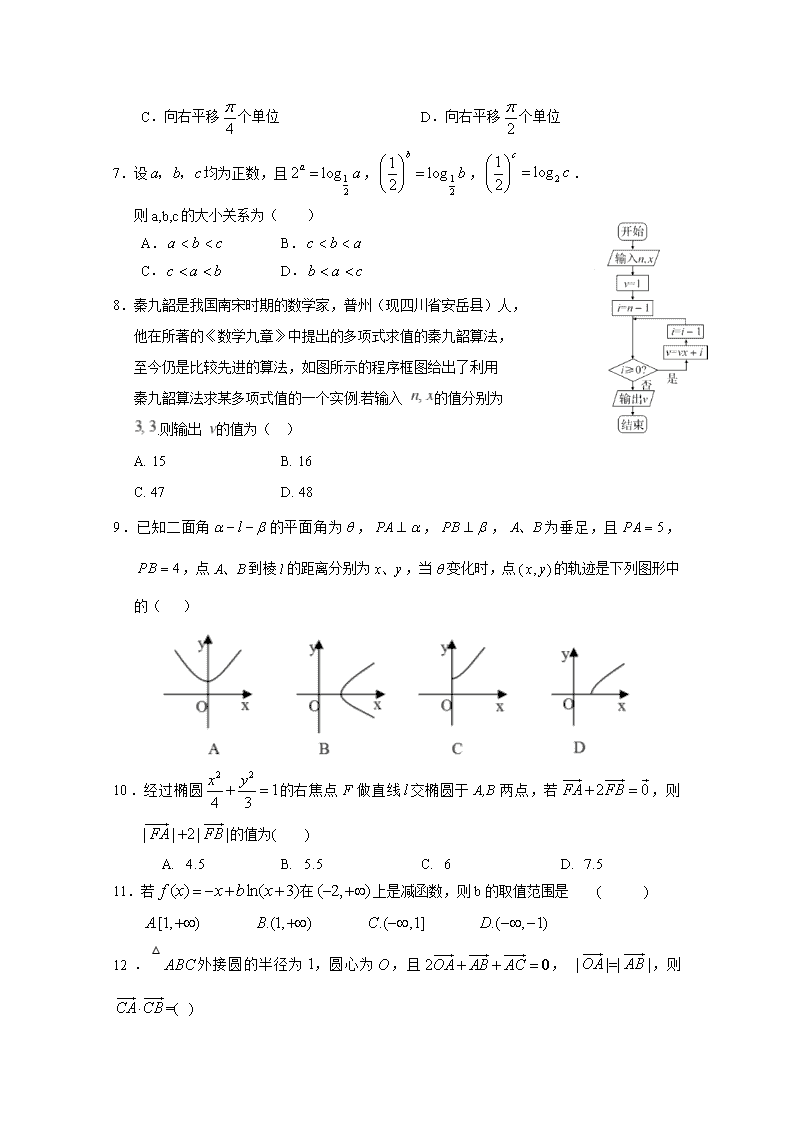
南宁三中2017~2018学年度下学期高二月考（三）‎ 数学（理）试题 考试时间:2018年5月28日(15:00—17:00)‎ 一、选择题(每小题只有一个正确答案,请将其填在答题卷的相应位置,每小题5分,共60分)‎ ‎1．已知全集，集合，，则（ ）‎ ‎ A． B．‎ ‎ C．或 D．‎ ‎2．若复数（）为纯虚数，则等于( )‎ A. 0 B. 1 C. -1 D. 0或1‎ ‎3．某产品的广告费用x与销售额y的统计数据如下表：‎ 广告费用x(万元)‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y(万元)‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程＝x＋中的为9.4，据此模型预报广告费用为6万元时销售额为(　)‎ A．63.6万元 　　 B．65.5万元　　　 C．67.7万元 　 D．72.0万元 ‎4．从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张不能从事前两项工作，其余四人均能从事这四项工作，则不同的选派方案共有（ ） ‎ A. 36种 B. 12种 C. 48种 D.72种 ‎5．已知双曲线的一条准线经过抛物线的焦点，则该双曲线的渐近线方程为 （ ）‎ ‎ A． B． C． D．‎ ‎6．为了得到函数的图象,只需把函数的图象（ ）‎ A．向左平移个单位 B．向左平移个单位 C．向右平移个单位 D．向右平移个单位 ‎7．设均为正数，且，，．‎ 则a,b,c的大小关系为（ ）‎ ‎ A． B． ‎ ‎ C． D．‎ ‎8．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，‎ 他在所著的《数学九章》中提出的多项式求值的秦九韶算法，‎ 至今仍是比较先进的算法，如图所示的程序框图给出了利用 秦九韶算法求某多项式值的一个实例.若输入 的值分别为 ‎ ‎.则输出 的值为（   ）‎ A. 15                 B. 16                     ‎ C. 47                   D. 48 ‎ ‎9．已知二面角的平面角为，，，为垂足，且，，点到棱的距离分别为，当变化时，点的轨迹是下列图形中的（ ）‎ ‎10．经过椭圆的右焦点F做直线交椭圆于A,B两点，若，则的值为( )‎ A. ‎ B. C. D. ‎ ‎11．若在上是减函数，则b的取值范围是 ( )‎ ‎ ‎ ‎12．△外接圆的半径为，圆心为，且， ，则=( )‎ A. B. C. D. ‎ 二、填空题（每小题5分，共20分，请将答案填在答题卷的相应位置）‎ ‎13. 若不等式组表示的平面区域是一个三角形，则的取值范围是 ‎ ‎14 ．在等差数列中，已知，则其前11项的和= .‎ ‎15．已知函数， ，若对任意都有成立，则实数 的取值范围是 ‎ ‎16．如图，在六面体中，‎ ‎,设为正三棱锥外接 球的球心，为三棱锥内切球的球心，则 等于 ‎ ‎三、解答题(17题10分,其余每题12分,共70分,请将答案填在答题卷的相应位置)‎ ‎17．（本小题满分10分）在△ABC中，分别为角A、B、C的对边，，=3, △ABC的面积为6，D为△ABC内任一点，点D到三边距离之和为d。‎ ‎（1）求边b、c；‎ ‎（2）求d的取值范围。‎ ‎18．（本小题满分12分）已知数列的前项和为，且满足。‎ ‎（1）求数列的通项公式；‎ ‎（2）设，，求数列的前项和。‎ ‎19．（本小题满分12分）为了防止受到核污染的产品影响我国民众的身体健康，要求产品在进入市场前必须进行两轮核辐射检测，只有两轮都合格才能进行销售，否则不能销售.已知某产品第一轮检测不合格的概率为，第二轮检测不合格的概率为，两轮检测是否合格相互没有影响.‎ ‎（1）求该产品不能销售的概率；‎ ‎（2）如果产品可以销售，则每件产品可获利40元；如果产品不能销售，则每件产品亏损80元（即获利元）.已知一箱中有产品4件，记一箱产品获利X元，求X的分布列，并求出均值E(X).‎ ‎20．（本小题满分12分）如图，直角梯形ABCD中，AB∥CD，AB^AD，且CD=2AB=2AD=4，△ADP为等边三角形，二面角P—AD—B的对应的余弦值为，M为PD中点。‎ ‎ （1）求证：AM∥面PBC。 ‎ ‎ （2）求二面角A—PB—C的余弦值。‎ ‎21．（本小题满分12分）如图，已知椭圆 ，A,B是四条直线所围成的两个顶点 ‎（1）设P是椭圆C上任意一点，若 ，求证：动点在定圆上运动，并求出定圆的方程.‎ O M A N B x y ‎（2）若M,N是椭圆C上两个动点，且直线OM,ON斜率之积等于OA,OB斜率之积，试探求的面积是否为定值，说明理由 ‎22 ．（本小题满分12分）已知函数（）的图像在点处的切线方程为，‎ ‎ （1）用表示出；‎ ‎ （2）若在恒成立，求实数的取值范围；‎ ‎（3）证明：‎ 南宁三中2017~2018学年度下学期高二月考（三）‎ 数学（理）试题答案 一、选择题（每小题5分，共60分，每小题只有一个正确答案）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B B B D A C A D C A C C 二、填空题（每小题5分，共20分）‎ ‎13 、 14 、 99 15、 16、0 ‎ 三、解答题(17题10分,其余每题12分,共70分)‎ ‎17.解：（Ⅰ）………3分 ‎，20 ……………………………………….5分 由及20与=3解得b=4，c=5或b=5,c= 4 ………………….6分 ‎(2)法一：设D到三边的距离分别为x、y、z，则 ……………8分 ‎ ‎ 又x、y满足…………………………………9分 画出不等式表示的平面区域，由线性规划可知： ………………………10分 法二：，所以，即，‎ ‎18. 解：(1)由得.（1分）‎ 当时，，（3分）（5分）‎ 数列是首项为，公比为的等比数列， ……………6分 ‎（2），‎ ‎（8分） …………10分 ‎ ……………12分 ‎19. 解：（1）记“该产品不能销售”为事件A，则 ‎.所以，该产品不能销售的概率为. ……….4分 ‎（2）由已知，可知X的取值为. ……………………..5分 ‎ ‎， ，‎ ‎，，‎ ‎. ……………………………..10分(每个1分)‎ 所以X的分布列为 X ‎-320‎ ‎-200‎ ‎-80‎ ‎40‎ ‎160‎ P 法一：E(X)….12分 A B C D M P 法二： 销售的个数，获利 ‎ ‎ ‎20. 解：（1）取PC的中点N，连结MN，BN 在△PDC中，MN为中位线， ‎ 又 ‎ 所以四边形ABMN为平行四边形，所以 又在平面PBC外，而BN在平面PBC内，所以 ‎………………………………………………..4分 ‎(2)法一： 以AD的中点O为坐标原点，OA为x轴，与AB平行的直线为y轴，过O点与xoy面垂直的直线为z轴建立空间直角坐标系如图……………………5分 则,‎ 设，因为……………6分 又，又平面PAD的一个法向量为，平面ABD的法向量为 依题意：‎ 故P的坐标为…………………..8分 从而 所以平面PAB的一个法向量为……………………9分 同理可求平面PBC的一个法向量为……………….10分 设二面角A-PB-C的平面角为 ，由图可见为钝角 所以…………..12分 ‎21.解：（1）易求，……………………………………….1分 设，则，由有 ‎，所以，，即……4分 故点在定圆上。………………………………………….5分 ‎（2）法一：设，，则，平方得，‎ ‎，即……………………7分 直线的方程为 …………8分 则到直线的距离………………9分 ‎……..10分 故三角形的面积为定值…………………………………………………….12分 法二：设，则 ‎ 即 面积 法三：椭圆伸缩变换成圆 法四：，‎ 同理，（舍负）‎ ‎22. 解： （1），则有，解得　 ……2分 ‎ （2）由（1）知，，‎ ‎ 令，……………4分 ‎ 则 ，‎ ‎ （i）当 ，‎ ‎ 若 ，则，是减函数，所以 ‎ ，故在上恒不成立。‎ ‎ （ii）时， 若，故当时，‎ ‎ 综上所述，所求的取值范围为 ……………………8分 ‎（3）解法一：由（2）知：当时，有。‎ ‎ 令，有 当时，。‎ ‎ 令，有 即 ， 将上述个不等式一次相加 ‎ 整理得 ‎ 解法二：用数学归纳法证明 ‎（1）当时，左边，右边，不等式成立 ‎（2）假设时，不等式成立，就是　‎ 那么 由（2）知：当时，有，令，有 令，得：‎ 就是说， 当时，不等式也成立。‎ 根据（1）和（2），可知不等式对任何都成立。……………………12分