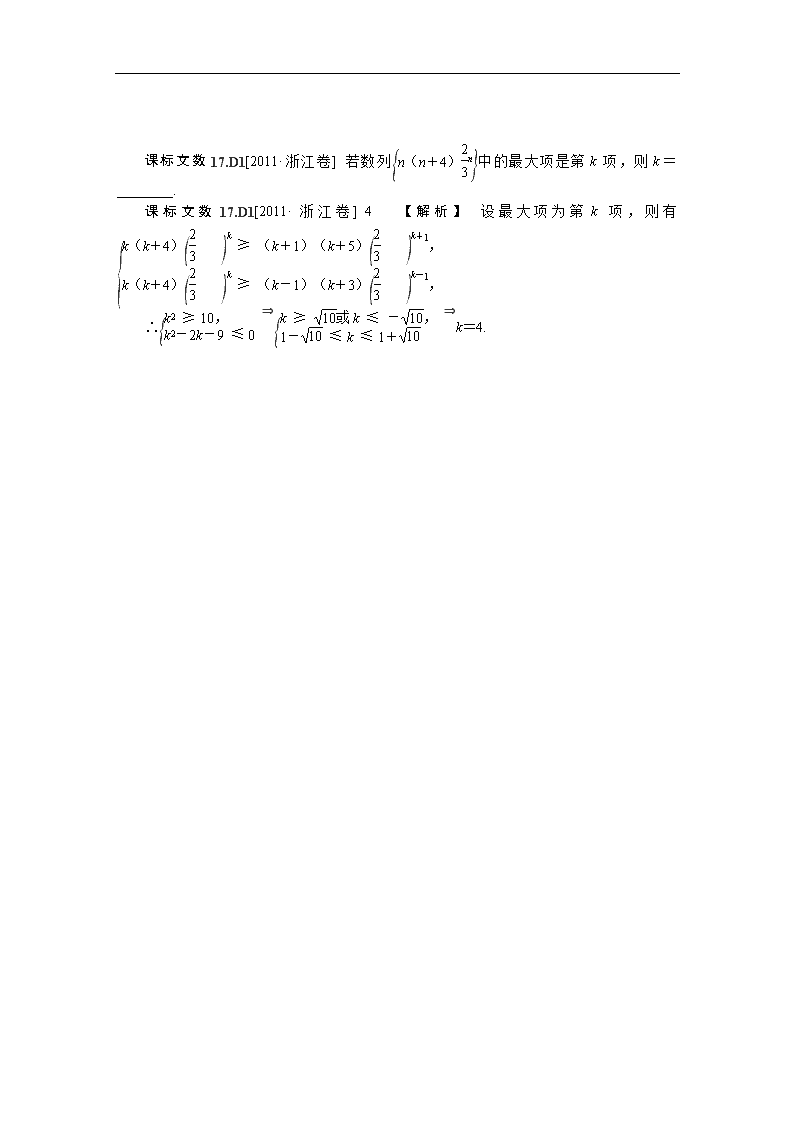2011年高考数学真题分类汇编D
课标文数 17.D1[2011·浙江卷] 若数列 {n(n+4)2
3
n}中的最大项是第 k 项,则 k=
________.
课 标 文 数 17.D1[2011· 浙 江 卷 ] 4 【 解 析 】 设 最 大 项 为 第 k 项 , 则 有
{k(k+4)(2
3 )k
≥ (k+1)(k+5)(2
3 )k+1
,
k(k+4)(2
3 )k
≥ (k-1)(k+3)(2
3 )k-1
,
∴{k2 ≥ 10,
k2-2k-9 ≤ 0 ⇒{k ≥ 10或 k ≤ - 10,
1- 10 ≤ k ≤ 1+ 10 ⇒k=4.
课标文数 20.D2,A2[2011·北京卷] 若数列 An:a1,a2,…,an(n≥2)满足|ak+1-ak|=1(k
=1,2,…,n-1),则称 An 为 E 数列.记 S(An)=a1+a2+…+an.
(1)写出一个 E 数列 A5 满足 a1=a3=0;
(2)若 a1=12,n=2000,证明:E 数列 An 是递增数列的充要条件是 an=2011;
(3)在 a1=4 的 E 数列 An 中,求使得 S(An)=0 成立的 n 的最小值.
课标文数 20.D2,A2[2011·北京卷] 【解答】 (1)0,1,0,1,0 是一个满足条件的 E 数
列 A5.
(答案不唯一,0,-1,0,1,0;0,±1,0,1,2;0,±1,0,-1,-2;0,±1,0,-
1,0 都是满足条件的 E 数列 A5)
(2)必要性:因为 E 数列 An 是递增数列,
所以 ak+1-ak=1(k=1,2,…,1999).
所以 An 是首项为 12,公差为 1 的等差数列.
所以 a2000=12+(2000-1)×1=2011,
充分性:由于 a2000-a1999≤1.
a1999-a1998≤1.
……
a2-a1≤1.
所以 a2000-a1≤1999,即 a2000≤a1+1999.
又因为 a1=12,a2000=2011.
所以 a2000=a1+1999.
故 ak+1-ak=1>0(k=1,2,…,1999),即 E 数列 An 是递增数列.
综上,结论得证.
(3)对首项为 4 的 E 数列 An,由于
a2≥a1-1=3,
a3≥a2-1≥2,
……
a8≥a7-1≥-3,
……
所以 a1+a2+…+ak>0(k=2,3,…,8).
所以对任意的首项为 4 的 E 数列 An,若 S(An)=0,则必有 n≥9.
又 a1=4 的 E 数列 A9:4,3,2,1,0,-1,-2,-3,-4 满足 S(A9)=0,
所以 n 的最小值是 9.
大纲理数 4.D2[2011·全国卷] 设 Sn 为等差数列{an}的前 n 项和,若 a1=1,公差 d=2,Sk
+2-Sk=24,则 k=( )
A.8 B.7 C.6 D.5
大纲理数 4.D2[2011·全国卷] D 【解析】 ∵Sk+2-Sk=ak+1+ak+2=2a1+(2k+1)d=4k
+4,∴4k+4=24,可得 k=5,故选 D.
大纲理数 20.D2,D4[2011·全国卷] 设数列{an}满足 a1=0 且 1
1-an+1- 1
1-an=1.
(1)求{an}的通项公式;
(2)设 bn=1- an+1
n
,记 Sn=
n
∑
k=1
bk,证明:Sn<1.
大纲理数 20.D2,D4[2011·全国卷] 【解答】 (1)由题设 1
1-an+1- 1
1-an=1,
即{ 1
1-an}是公差为 1 的等差数列.
又 1
1-a1=1,故 1
1-an=n.
所以 an=1-1
n.
(2)证明:由(1)得
bn=1- an+1
n
= n+1- n
n+1· n
= 1
n
- 1
n+1
,
∴Sn=∑
n
k=1bk=∑
n
k=1( 1
k
- 1
k+1)=1- 1
n+1<1.
大纲文数 6.D2[2011·全国卷] 设 Sn 为等差数列{an}的前 n 项和,若 a1=1,公差 d=2,Sk
+2-Sk=24,则 k=( )
A.8 B.7
C.6 D.5
大纲文数 6.D2[2011·全国卷] D 【解析】 ∵S k+2-Sk=ak+1+ak+2=2a1+(2k+1)d=4k
+4,∴4k+4=24,可得 k=5,故选 D.
课标理数 10.M1,D2,B11[2011·福建卷] 已知函数 f(x)=ex+x.对于曲线 y=f(x)上横坐标
成等差数列的三个点 A、B、C,给出以下判断:
①△ABC 一定是钝角三角形;
②△ABC 可能是直角三角形;
③△ABC 可能是等腰三角形;
④△ABC 不可能是等腰三角形.
其中,正确的判断是( )
A.①③ B.①④
C.②③ D.②④
课标理数 10.M1,D2,B11[2011·福建卷] B 【解析】 解法一:(1)设 A、B、C 三点的
横坐标分别为 x1,x2,x3(x1
0,
∴ f(x)在(-∞,+∞)上是增函数,
∴ f(x1)0,
∴ f(x)在(-∞,+∞)上是增函数,画出 f(x)的图象(大致).
∴ f(x1)0,0<φ<π)在 x=
π
6 处取得最大值,且最大值为 a3,求函
数 f(x)的解析式.
课标数学 16.D3,C4[2011·福建卷] 【解答】 (1)由 q=3,S 3=13
3 得a1(1-33)
1-3 =13
3 ,
解得 a1=1
3.
所以 an=1
3×3n-1=3n-2.
(2)由(1)可知 an=3n-2,所以 a3=3.
因为函数 f(x)的最大值为 3,所以 A=3;
因为当 x=
π
6 时 f(x)取得最大值,
所以 sin(2 ×
π
6 +φ)=1.
又 0<φ<π,故 φ=
π
6 .
所以函数 f(x)的解析式为 f(x)=3sin(2x+
π
6 ).
课标文数 16.D3[2011·福建卷] 商家通常依据“乐观系数准则”确定商品销售价格,即根
据商品的最低销售限价 a,最高销售限价 b(b>a)以及实数 x(0a,b-a≠0,
∴x2=1-x,即 x2+x-1=0,
解得 x=
-1 ± 5
2 ,
因为 00),b1-a1=
1,b2-a2=2,b3-a3=3.
(1)若 a=1,求数列{an}的通项公式;
(2)若数列{an}唯一,求 a 的值.
课标理数 18.D3[2011·江西卷] 【解答】 (1)设{an}的公比为 q,则 b1=1+a=2,b2=2+
aq=2+q,b3=3+aq2=3+q2,
由 b1,b2,b3 成等比数列得(2+q)2=2(3+q2),
即 q2-4q+2=0,解得 q1=2+ 2,q2=2- 2,
所以{an}的通项公式为 an=(2+ 2)n-1 或 an=(2- 2)n-1.
(2)设{an}的公比为 q,则由(2+aq)2=(1+a)(3+aq2),得 aq2-4aq+3a-1=0,(*)
由 a>0 得 Δ=4a2+4a>0,故方程(*)有两个不同的实根,
由{an}唯一,知方程(*)必有一根为 0,代入(*)得 a=1
3.
课标文数 5.D3[2011·辽宁卷] 若等比数列{an}满足 anan+1=16n,则公比为( )
A.2 B.4 C.8 D.16
课标文数 5.D3[2011·辽宁卷] B 【解析】 由于 a nan+1 =16n,又 an-1an=16n-1 ,所以
anan+1
an-1an=q2=16,又由 anan+1=16n 知 an>0,所以 q=4.
课标文数 17.D2,D3[2011·课标全国卷] 已知等比数列{an}中,a1=1
3,公比 q=1
3.
(1)Sn 为{an}的前 n 项和,证明:Sn=1-an
2 ;
(2)设 bn=log3a1+log3a2+…+log3an,求数列{bn}的通项公式.
课标文数 17.D2,D3[2011·课标全国卷] 【解答】 (1)因为 an=1
3×(1
3 )n-1
= 1
3n,
Sn=
1
3(1- 1
3n)
1-1
3
=
1- 1
3n
2 ,
所以 Sn=1-an
2 .
(2)bn=log3a1+log3a2+…+log3an
=-(1+2+…+n)
=-n(n+1)
2 .
所以{bn}的通项公式为 bn=-n(n+1)
2 .
大纲文数 9.D3[2011·四川卷] 数列{an}的前 n 项和为 Sn,若 a1=1,an+1=3Sn(n≥1),则
a6=( )
A.3×44 B.3×44+1
C.44 D.44+1
大纲文数 9.D3[2011·四川卷] A 【解析】 由 an+1=3Sn⇒Sn+1-Sn=3Sn⇒Sn+1=4Sn,所
以数列{Sn}是首项为 1,公比为 4 的等比数列,所以 Sn=4n-1,所以 a6=S6-S5=45-44=3×
44,所以选择 A.
大纲理数 11.D2[2011·重庆卷] 在等差数列{a n}中,a 3+a7=37,则 a 2+a4+a6+a8=
________.
大纲理数 11.D2[2011·重庆卷] 74 【解析】 由 a3+a7=37,得(a1+2d)+(a1+6d)=37,
即 2a1+8d=37.∴a2+a4+a6+a8=(a1+d)+(a1+3d)+(a1+5d)+(a1+7d)=2(2a1+8d)=74.
课标文数 7.D4[2011·安徽卷] 若数列{an}的通项公式是 an=(-1)n(3n-2),则 a1+a2+…
+a10=( )
A.15 B.12
C.-12 D.-15
课标文数 7.D4[2011·安徽卷] A 【解析】 a 1+a2+…+a10=-1+4-7+10+…+(-
1)10·(3×10-2)=(-1+4)+(-7+10)+…+[(-1) 9·(3×9-2)+(-1) 10·(3×10-2)]=3
×5=15.
课标文数 21.D3,D4[2011·安徽卷] 在数 1 和 100 之间插入 n 个实数,使得这 n+2 个数
构成递增的等比数列,将这 n+2 个数的乘积记作 Tn,再令 an=lgTn,n≥1.
(1)求数列{an}的通项公式;
(2)设 bn=tanan·tanan+1,求数列{bn}的前 n 项和 Sn.
课标文数 21.D3,D4[2011·安徽卷] 本题考查等比和等差数列,指数和对数的运算,两角
差的正切公式等基本知识,考查灵活运用知识解决问题的能力,综合运算能力和创新思维能
力.
【解答】 (1)设 t1,t2,…,tn+2 构成等比数列,其中 t1=1,tn+2=100,则
Tn=t1·t2·…·tn+1·tn+2,①
Tn=tn+2·tn+1·…·t2·t1.②
①×②并利用 titn+3-i=t1tn+2=102(1≤i≤n+2),得
T2n=(t1tn+2)·(t2tn+1)·…·(t n+1t2)·(tn+2t1)=102(n+2),
∴an=lgTn=n+2,n≥1.
(2)由题意和(1)中计算结果,知
bn=tan(n+2)·tan(n+3),n≥1.
另一方面,利用 tan1=tan[(k+1)-k]= tan(k+1)-tank
1+tan(k+1)·tank.
得 tan(k+1)·tank=tan(k+1)-tank
tan1 -1.
所以 Sn=∑
n
bk= ∑
n+2
tan(k+1)·tank
= ∑
n+2
[tan(k+1)-tank
tan1 -1]=tan(n+3)-tan3
tan1 -n.
课标理数 18.D3,D4[2011·安徽卷]
在数 1 和 100 之间插入 n 个实数,使得这 n+2 个数构成递增的等比数列,将这 n+2 个
数的乘积记作 Tn,再令 an=lgTn,n≥1.
(1)求数列{an}的通项公式;
(2)设 bn=tanan·tanan+1,求数列{bn}的前 n 项和 Sn.
课标理数 18.D3,D4[2011·安徽卷] 【解析】 本题考查等比和等差数列,对数和指数的
运算,两角差的正切公式等基本知识,考查灵活运用基本知识解决问题的能力,运算求解能
力和创新思维能力.
【解答】 (1)设 t1,t2,…,tn+2 构成等比数列,其中 t1=1,tn+2=100,则
Tn=t1·t2·…·tn+1·tn+2,①
Tn=tn+2·tn+1·…·t2·t1,②
①×②并利用 titn+3-i=t1tn+2=102(1≤i≤n+2),得
T2n=(t1tn+2)·(t2tn+1)·…·(t n+1t2)·(tn+2t1)=102(n+2).
∴an=lgTn=n+2,n≥1.
(2)由题意和(1)中计算结果,知
bn=tan(n+2)·tan(n+3),n≥1,
另一方面,利用
tan1=tan[(k+1)-k]= tan(k+1)-tank
1+tan(k+1)·tank,
得 tan(k+1)·tank=tan(k+1)-tank
tan1 -1.
=tan(n+3)-tan3
tan1 -n.
大纲理数 20.D2,D4[2011·全国卷] 设数列{an}满足 a1=0 且 1
1-an+1- 1
1-an=1.
(1)求{an}的通项公式;
(2)设 bn=1- an+1
n
,记 Sn=
n
∑
k=1
bk,证明:Sn<1.
大纲理数 20.D2,D4[2011·全国卷] 【解答】 (1)由题设 1
1-an+1- 1
1-an=1,
即{ 1
1-an}是公差为 1 的等差数列.
又 1
1-a1=1,故 1
1-an=n.
所以 an=1-1
n.
(2)证明:由(1)得
bn=1- an+1
n
= n+1- n
n+1· n
= 1
n
- 1
n+1
,
∴Sn=∑
n
k=1bk=∑
n
k=1( 1
k
- 1
k+1)=1- 1
n+1<1.
课标文数 20.D4[2011·湖南卷] 某企业在第 1 年初购买一台价值为 120 万元的设备 M,M
的价值在使用过程中逐年减少,从第 2 年到第 6 年,每年初 M 的价值比上年初减少 10 万元;
从第 7 年开始,每年初 M 的价值为上年初的 75%.
(1)求第 n 年初 M 的价值 an 的表达式;
(2)设 An=a1+a2+…+an
n .若 An 大于 80 万元,则 M 继续使用,否则须在第 n 年初对 M
更新.证明:须在第 9 年初对 M 更新.
课标文数 20.D4[2011·湖南卷] 【解答】 (1)当 n≤6 时,数列{an}是首项为 120,公差为
-10 的等差数列.
an=120-10(n-1)=130-10n;
当 n≥6 时,数列{an}是以 a6 为首项,公比为3
4的等比数列,又 a6=70,所以 an=70×
(3
4 )n-6
.
因此,第 n 年初,M 的价值 an 的表达式为
an={130-10n,n ≤ 6,
70 × (3
4 )n-6
,n ≥ 7.
(2)设 Sn 表示数列{an}的前 n 项和,由等差及等比数列的求和公式得
当 1≤n≤6 时,Sn=120n-5n(n-1),
An=120-5(n-1)=125-5n;
当 n≥7 时,由于 S6=570,故
Sn=S6+(a7+a8+…+an)=570+70×3
4×4×[1-(3
4 )n-6
]=780-210×(3
4 )n-6
,
An=
780-210 × (3
4 )n-6
n ,
因为{an}是递减数列,所以{An}是递减数列.又
A8=
780-210 × (3
4 )2
8 =8247
64>80,
A9=
780-210 × (3
4 )3
9 =7679
96<80,
所以须在第 9 年初对 M 更新.
课标理数 5.D4[2011·江西卷] 已知数列{a n}的前 n 项和 Sn 满足:Sn+Sm=Sn+m,且 a1=
1.那么 a10=( )
A.1 B.9
C.10 D.55
课标理数 5.D4[2011·江西卷] A 【解析】 方法一:由 Sn+Sm=Sn+m,得 S1+S9=S10,
∴a10=S10-S9=S1=a1=1,故选 A.
方法二:
∵S2=a1+a2=2S1,∴a2=1,
∵S3=S1+S2=3,∴a3=1,
∵S4=S1+S3=4,∴a4=1,
由此归纳 a10=1,故选 A.
课标理数 17.D4[2011·辽宁卷]
已知等差数列{an}满足 a2=0,a6+a8=-10.
(1)求数列{an}的通项公式;
(2)求数列{ an
2n-1 }的前 n 项和.
课标理数 17.D4[2011·辽宁卷] 【解答】 (1)设等差数列{an}的公差为 d,由已知条件可得
{a1+d=0,
2a1+12d=-10.解得{a1=1,
d=-1.
故数列{an}的通项公式为 an=2-n.
(2)设数列{ an
2n-1 }的前 n 项和为 Sn,即 Sn=a1+a2
2 +…+ an
2n-1,故 S1=1,
Sn
2 =a1
2 +a2
4 +…+an
2n.
所以,当 n>1 时,
Sn
2 =a1+a2-a1
2 +…+an-an-1
2n-1 -an
2n
=1-(1
2+1
4+…+ 1
2n-1)-2-n
2n
=1-(1- 1
2n-1)-2-n
2n
= n
2n,
所以 Sn= n
2n-1.
综上,数列{ an
2n-1 }的前 n 项和 Sn= n
2n-1.
课标理数 14.D4[2011·陕西卷] 植树节某班 20 名同学在一段直线公路一侧植树,每人植
一棵,相邻两棵树相距 10 米,开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自
树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为________(米).
课标理数 14.D4[2011·陕西卷] 2000 【解析】 树苗放在 10 或 11 号坑,则其余的十九人
一次走过的路程为 90,80,70,60,…,80,90,100,则和为 s=[9(10+90)
2 × 2+100]
×2=2000,若放在 11 号坑,结果一样.
课标理数 19.B11,D4[2011·陕西卷]
图 1-11
如图 1-11,从点 P1(0,0)作 x 轴的垂线交曲线 y=ex 于点 Q1(0,1),曲线在 Q1 点处的
切线与 x 轴交于点 P2.现从 P2 作 x 轴的垂线交曲线于点 Q2,依次重复上述过程得到一系列点:
P1,Q1;P2,Q2;…;Pn,Qn,记 Pk 点的坐标为(xk,0)(k=1,2,…,n).
(1)试求 xk 与 xk-1 的关系(2≤k≤n);
(2)求|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|.
课标理数 19.B11,D4[2011·陕西卷] 【解答】
(1)设 Pk-1(xk-1,0),由 y′=ex 得 Qk-1(xk-1,exk-1)点处切线方程为 y-exk-1=exk-1(x-xk
-1),
由 y=0 得 xk=xk-1-1(2≤k≤n).
(2)由 x1=0,xk-xk-1=-1,得 xk=-(k-1),
所以|PkQk|=exk=e-(k-1),于是
Sn=|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|
=1+e-1+e-2+…+e-(n-1)=1-e-n
1-e-1=e-e1-n
e-1 .
课标文数 10.D4[2011·陕西卷] 植树节某班 20 名同学在一段直线公路一侧植树,每人植
一棵,相邻两棵树相距 10 米,开始时需将树苗集中放置在某一树坑旁边,现将树坑从 1 到 20
依次编号,为使各位同学从各自树坑前来领取树苗所走的路程总和最小,树苗可以放置的两
个最佳坑位的编号为( )
A.①和⑳ B.⑨和⑩
C.⑨和⑪ D.⑩和⑪
课标文数 10.D4[2011·陕西卷] D 【解析】 从实际问题中考虑将树苗放在最中间的坑旁
边,则每个人所走的路程和最小,一共 20 个坑,为偶数,在中间的有两个坑为 10 和 11 号坑,
故答案选 D.
课标文数 19.B11,D4[2011·陕西卷] 如图 1-12,从点 P1(0,0)作 x 轴的垂线交曲线 y=
ex 于点 Q1(0,1),曲线在 Q1 点处的切线与 x 轴交于点 P2.再从 P2 作 x 轴的垂线交曲线于点
Q2,依次重复
图 1-12
上述过程得到一系列点:P1,Q1;P2,Q2;…;Pn,Qn,记 Pk 点的坐标为(xk,0)(k=1,
2,…,n).
(1)试求 xk 与 xk-1 的关系(2≤k≤n);
(2)求|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|.
课标文数 19.B11,D4[2011·陕西卷] 【解答】 (1)设 Pk-1(xk-1,0),由 y′=ex 得 Qk-1(xk-
1,exk-1)点处切线方程为 y-exk-1=exk-1(x-xk-1),
由 y=0 得 xk=xk-1-1(2≤k≤n).
(2)由 x1=0,xk-xk-1=-1,得 xk=-(k-1),
所以|PkQk|=exk=e-(k-1),于是
Sn=|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|
=1+e-1+e-2+…+e-(n-1)=1-e-n
1-e-1=e-e1-n
e-1 .
大纲文数 16.D4[2011·重庆卷] 设{an}是公比为正数的等比数列,a1=2,a3=a2+4.
(1)求{an}的通项公式;
(2)设{bn}是首项为 1,公差为 2 的等差数列,求数列{an+bn}的前 n 项和 Sn.
大纲文数 16.D4[2011·重庆卷]
【解答】 (1)设 q 为等比数列{an}的公比,则由 a1=2,a3=a2+4 得 2q2=2q+4,即 q2-
q-2=0,解得 q=2 或 q=-1(舍去),因此 q=2.
所以{an}的通项为 an=2·2n-1=2n(n∈N*).
(2)Sn=2(1-2n)
1-2 +n×1+n(n-1)
2 ×2
=2n+1+n2-2.
课标理数 20.D5,A3[2011·北京卷] 若数列 An:a1,a2,…,an(n≥2)满足|ak+1-ak|=1(k
=1,2,…,n-1),则称 An 为 E 数列.记 S(An)=a1+a2+…+an.
(1)写出一个满足 a1=a5=0,且 S(A5)>0 的 E 数列 A5;
(2)若 a1=12,n=2000.证明:E 数列 An 是递增数列的充要条件是 an=2011;
(3)对任意给定的整数 n(n≥2),是否存在首项为 0 的 E 数列 An,使得 S(An)=0?如果存
在,写出一个满足条件的 E 数列 An;如果不存在,说明理由.
课标理数 20.D5,A3[2011·北京卷] 【解答】 (1)0,1,2,1,0 是一个满足条件的 E
数列 A5.
(答案不唯一,0,1,0,1,0 也是一个满足条件的 E 数列 A5)
(2)必要性:因为 E 数列 An 是递增数列,
所以 ak+1-ak=1(k=1,2,…,1999).
所以 An 是首项为 12,公差为 1 的等差数列.
所以 a2000=12+(2000-1)×1=2011.
充分性:由于 a2000-a1999≤1,
a1999-a1998≤1,
……
a2-a1≤1,
所以 a2000-a1≤1999,即 a2000≤a1+1999.
又因为 a1=12,a2000=2011,
所以 a2000=a1+1999,
故 ak+1-ak=1>0(k=1,2,…,1999),即 E 数列 An 是递增数列.
综上,结论得证.
(3)令 ck=ak+1-ak(k=1,2,…,n-1),则 ck=±1,
因为 a2=a1+c1,
a3=a1+c1+c2,
……
an=a1+c1+c2+…+cn-1,
所以 S(An)=na1+(n-1)c1+(n-2)c2+(n-3)c3+…+cn-1
=(n-1)+(n-2)+…+1-[(1-c1)(n-1)+(1-c2)·(n-2)+…+(1-cn-1)]
=n(n-1)
2 -[(1-c1)(n-1)+(1-c2)(n-2)+…+(1-cn-1)].
因为 ck=±1,所以 1-ck 为偶数(k=1,2,…,n-1),
所以(1-c1)(n-1)+(1-c2)(n-2)+…+(1-cn-1)为偶数,
所以要使 S(An)=0,必须使n(n-1)
2 为偶数,
即 4 整除 n(n-1),亦即 n=4m 或 n=4m+1(m∈N*).
当 n=4m(m∈N*)时,E 数列 An 的项满足 a4k-1=a4k-3=0,a4k-2=-1,a4k=1(k=1,
2,…,m)时,有 a1=0,S(An)=0;
当 n=4m+1(m∈N*)时,E 数列 An 的项满足 a4k-1=a4k-3=0,a4k-2=-1,a4k=1(k=1,
2,…,m),a4m+1=0 时,有 a1=0,S(An)=0;
当 n=4m+2 或 n=4m+3(m∈N*)时,n(n-1)不能被 4 整除,此时不存在 E 数列 An,使
得 a1=0,S(An)=0.
课标理数 20.D5[2011·广东卷] 设 b>0,数列{an}满足 a1=b,an= nban-1
an-1+2n-2(n≥2).
(1)求数列{an}的通项公式;
(2)证明:对于一切正整数 n,an≤bn+1
2n+1+1.
课标理数 20.D5[2011·广东卷] 【解答】 (1)由 a1=b>0,知 an= nban-1
an-1+2n-2>0, n
an=1
b+
2
b·n-1
an-1.
令 An= n
an,A1=1
b,
当 n≥2 时,An=1
b+2
bAn-1
=1
b+ 2
b2+…+2n-2
bn-1+2n-1
bn-1A1
=1
b+ 2
b2+…+2n-2
bn-1+2n-1
bn .
①当 b≠2 时,
An=
1
b[1-(2
b )n
]
1-2
b
= bn-2n
bn(b-2);
②当 b=2 时,An=n
2.
∴an={nbn(b-2)
bn-2n ,b ≠ 2,
2, b=2.
(2)证明:当 b≠2 时,欲证 an=nbn(b-2)
bn-2n ≤bn+1
2n+1+1,只需证 nbn≤(bn+1
2n+1+1)bn-2n
b-2 ,
即证(2n+1+bn+1)bn-2n
b-2 ≥n·2n+1bn.
而(2n+1+bn+1)bn-2n
b-2 =(2n+1+bn+1)(bn-1+2bn-2+…+2n-1)
=2n+1bn-1+2n+2bn-2+…+22n+b2n+2b2n-1+…+2n-1bn+1
=2nbn(2
b+22
b2+…+2n
bn+bn
2n+bn-1
2n-1+…+b
2)
>2nbn(2+2+…+2)=2n·2nbn=n·2n+1bn,
∴an=nbn(b-2)
bn-2n <1+bn+1
2n+1.
当 b=2 时,an=2=bn+1
2n+1+1.
综上所述,an≤bn+1
2n+1+1.
课标文数 20.D5,E7[2011·广东卷]
设 b>0,数列{an}满足 a1=b,an= nban-1
an-1+n-1(n≥2).
(1)求数列{an}的通项公式;
(2)证明:对于一切正整数 n,2an≤bn+1+1.
课标文数 20.D5,E7[2011·广东卷] 【解答】 (1)由 a1=b>0,知 an= nban-1
an-1+n-1>0,
n
an=1
b+1
b·n-1
an-1.
令 An= n
an,A1=1
b,
当 n≥2 时,An=1
b+1
bAn-1
=1
b+…+ 1
bn-1+ 1
bn-1A1
=1
b+…+ 1
bn-1+ 1
bn.
①当 b≠1 时,An=
1
b(1- 1
bn)
1-1
b
= bn-1
bn(b-1),
②当 b=1 时,An=n.
∴an={nbn(b-1)
bn-1 ,b ≠ 1,
1, b=1.
(2)证明:当 b≠1 时,欲证 2an=2nbn(b-1)
bn-1 ≤bn+1+1,只需证 2nbn≤(bn+1+1)bn-1
b-1 .
∵(bn+1+1)bn-1
b-1 =b2n+b2n-1+…+bn+1+bn-1+bn-2+…+1
=bn(bn+ 1
bn+bn-1+ 1
bn-1+…+b+1
b)
>bn(2+2+…+2)
=2nbn,
∴2an=2nbn(b-1)
bn-1 <1+bn+1.
当 b=1 时,2an=2=bn+1+1.
综上所述 2an≤bn+1+1.
课标文数 21.D5[2011·江西卷] (1)已知两个等比数列{an},{bn},满足 a1=a(a>0),b1-a1
=1,b2-a2=2,b3-a3=3,若数列{an}唯一,求 a 的值;
(2)是否存在两个等比数列{an},{bn},使得 b1-a1,b2-a2,b3-a3,b4-a4 成公差不为 0
的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.
课标文数 21.D5[2011·江西卷] 【解答】 (1)设{an}的公比为 q,则 b1=1+a,b2=2+aq,
b3=3+aq2,
由 b1,b2,b3 成等比数列得(2+aq)2=(1+a)(3+aq2),
即 aq2-4aq+3a-1=0.
由 a>0 得 Δ=4a2+4a>0,故方程有两个不同的实根,
再由{an}唯一,知方程必有一根为 0,
将 q=0 代入方程得 a=1
3.
(2)假设存在两个等比数列{an},{bn}使 b1-a1,b2-a2,b3-a3,b4-a4 成公差不为 0 的
等差数列,设{an}的公比为 q1,{bn}的公比为 q2,
则 b2-a2=b1q2-a1q1,
b3-a3=b1q22-a1q21,
b4-a4=b1q32-a1q31,
由 b1-a1,b2-a2,b3-a3,b4-a4 成等差数列得
{2(b1q2-a1q1)=b1-a1+(b1q-a1q),
2(b1q-a1q)=b1q2-a1q1+(b1q-a1q),
即{b1(q2-1)2-a1(q1-1)2=0, ①
b1q2(q2-1)2-a1q1(q1-1)2=0, ②
①×q2-②得 a1(q1-q2)(q1-1)2=0.
由 a1≠0 得 q1=q2 或 q1=1,
i)当 q1=q2 时,由①②得 b1=a1 或 q1=q2=1,这时(b2-a2)-(b1-a1)=0,与公差不为 0
矛盾;
ii)当 q1=1 时,由①②得 b1=0 或 q2=1,这时(b2-a2)-(b1-a1)=0,与公差不为 0 矛
盾.
综上所述,不存在两个等比数列{an},{bn}使 b1-a1,b2-a2,b3-a3,b4-a4 成公差不
为 0 的等差数列.
课标理数 17.D5[2011·课标全国卷] 等比数列{an}的各项均为正数,且 2a1+3a2=1,a23=
9a2a6.
(1)求数列{an}的通项公式;
(2)设 bn=log3a1+log3a2+…+log3an,求数列{ 1
bn }的前 n 项和.
课标理数 17.D5[2011·课标全国卷] 【解答】 (1)设数列{an}的公比为 q,由 a23=9a2a6 得
a23=9a24,所以 q2=1
9.
由条件可知 q>0,故 q=1
3.
由 2a1+3a2=1 得 2a1+3a1q=1,所以 a1=1
3.
故数列{an}的通项公式为 an= 1
3n.
(2)bn=log3a1+log3a2+…+log3an
=-(1+2+…+n)
=-n(n+1)
2 .
故 1
bn=- 2
n(n+1)=-2(1
n- 1
n+1),
1
b1+ 1
b2+…+ 1
bn=-2(1-1
2 )+(1
2-1
3 )+…+(1
n- 1
n+1)=- 2n
n+1.
所以数列{ 1
bn }的前 n 项和为- 2n
n+1.
课标理数 20.D5[2011·山东卷] 等比数列{a n}中,a1,a2,a3 分别是下表第一、二、三行
中的某一个数,且 a1,a2,a3 中的任何两个数不在下表的同一列.
第一列 第二列 第三列
第一行 3 2 10
第二行 6 4 14
第三行 9 8 18
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nlnan,求数列{bn}的前 n 项和 Sn.
课标理数 20.D5[2011·山东卷] 【解答】 (1)当 a1=3 时,不合题意;
当 a1=2 时,当且仅当 a2=6,a3=18 时,符合题意;
当 a1=10 时,不合题意.
因此 a1=2,a2=6,a3=18,
所以公比 q=3,
故 an=2·3n-1.
(2)因为 bn=an+(-1)nlnan
=2·3n-1+(-1)nln(2·3n-1)
=2·3n-1+(-1)n[ln2+(n-1)ln3]
=2·3n-1+(-1)n(ln2-ln3)+(-1)nnln3,
所以
Sn=2(1+3+…+3 n-1)+[-1+1-1+…+(-1) n]·(ln2-ln3)+[-1+2-3+…+(-
1)nn]ln3.
所以
当 n 为偶数时,Sn=2·1-3n
1-3 +n
2ln3
=3n+n
2ln3-1;
当 n 为奇数时,Sn=2×1-3n
1-3 -(ln2-ln3)+(n-1
2 -n)ln3
=3n-n-1
2 ln3-ln2-1.
综上所述,Sn={3n+n
2ln3-1,n为偶数,
3n-n-1
2 ln3-ln2-1,n为奇数.
课标文数 20.D5[2011·山东卷] 等比数列{a n}中,a1,a2,a3 分别是下表第一、二、三行
中的某一个数,且 a1,a2,a3 中的任何两个数不在下表的同一列.
第一列 第二列 第三列
第一行 3 2 10
第二行 6 4 14
第三行 9 8 18
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nlnan,求数列{bn}的前 2n 项和 S2n.
课标文数 20.D5[2011·山东卷] 【解答】 (1)当 a1=3 时,不合题意;
当 a1=2 时,当且仅当 a2=6,a3=18 时,符合题意;
当 a1=10 时,不合题意.
因此 a1=2,a2=6,a3=18,所以公比 q=3.
故 an=2·3n-1.
(2)因为 bn=an+(-1)nlnan
=2·3n-1+(-1)nln(2·3n-1)
=2·3n-1+(-1)n[ln2+(n-1)ln3]
=2·3n-1+(-1)n(ln2-ln3)+(-1)nnln3,
所以 S2n=b1+b2+…+b2n
=2(1+3+…+3 2n-1 )+[-1+1-1+…+(-1) 2n](ln2-ln3)+[-1+2-3+…+(-
1)2n2n]ln3
=2×1-32n
1-3 +nln3
=32n+nln3-1.
课标数学 13.D5[2011·江苏卷] 设 1=a1≤a2≤…≤a7,其中 a1,a3,a5,a7 成公比为 q 的
等比数列,a2,a4,a6 成公差为 1 的等差数列,则 q 的最小值是________.
课标数学 13.D5[2011·江苏卷] 3 3 【解析】 记 a2=m,则 1≤m≤q≤m+1≤q2≤m+2≤
q3,
要 q 取最小值,则 m 必定为 1,于是有 1≤q≤2,2≤q2≤3,3≤q3,所以 q≥3 3.
课标数学 20.D5[2011·江苏卷] 设 M 为部分正整数组成的集合,数列{an}的首项 a1=1,
前 n 项的和为 Sn,已知对任意的整数 k∈M,当整数 n>k 时,S n+k +Sn-k =2(Sn+Sk)都成
立.
(1)设 M={1},a2=2,求 a5 的值;
(2)设 M={3,4},求数列{an}的通项公式.
课标数学 20.D5[2011·江苏卷] 本题考查数列的通项与前 n 项和的关系、等差数列的基本
性质等基础知识,考查考生分析探究及逻辑推理的能力.
【解答】 (1)由题设知,当 n≥2 时,Sn+1+Sn-1=2(Sn+S1),即(Sn+1-Sn)-(Sn-Sn-1)=
2S1.
从而 an+1-an=2a1=2.
又 a2=2,故当 n≥2 时,an=a2+2(n-2)=2n-2.
所以 a5 的值为 8.
(2)由题设知,当 k∈M={3,4}且 n>k 时,Sn+k+Sn-k=2Sn+2Sk 且 Sn+1+k+Sn+1-k=2Sn
+1+2Sk,两式相减得 an+1+k+an+1-k=2an+1,即 an+1+k-an+1=an+1-an+1-k.所以当 n≥8
时,an-6,an-3,an,an+3,an+6 成等差数列,且 an-6,an-2,an+2,an+6 也成等差数列.
从而当 n≥8 时,2an=an+3+an-3=an+6+an-6,(*)
且 an+6+an-6=an+2+an-2,所以当 n≥8 时,2an=an+2+an-2,即 an+2-an=an-an-2,
于是当 n≥9 时,an-3,an-1,an+1,an+3 成等差数列,从而 an+3+an-3=an+1+an-1,故由(*)
式知 2an=an+1+an-1,即 an+1-an=an-an-1.
当 n≥9 时,设 d=an-an-1.
当 2≤m≤8 时,m+6≥8,从而由(*)式知 2am+6=am+am+12,故 2am+7=am+1+am+13.
从而 2(am+7-am+6)=am+1-am+(am+13-am+12),
于是 am+1-am=2d-d=d.
因此,an+1-an=d 对任意 n≥2 都成立.又由 Sn+k+S n-k-2Sn=2Sk(k∈{3,4})可知(Sn
+k-Sn)-(Sn-Sn-k)=2Sk,故 9d=2S3 且 16d=2S4,解得 a4=7
2d,从而 a2=3
2d,a1=d
2.因此,
数列{an}为等差数列.
由 a1=1 知 d=2.
所以数列{an}的通项公式为 an=2n-1.
大纲文数 20.D5[2011·四川卷] 已知{a n}是以 a 为首项,q 为公比的等比数列,Sn 为它的
前 n 项和.
(1)当 S1、S3、S4 成等差数列时,求 q 的值;
(2)当 Sm、Sn、Sl 成等差数列时,求证:对任意自然数 k,am+k,an+k,al+k 也成等差数
列.
大纲文数 20.D5[2011·四川卷] 【解答】 (1)由已知,an=aqn-1,因此
S1=a,S3=a(1+q+q2),S4=a(1+q+q2+q3).
当 S1,S3,S4 成等差数列时,S4-S3=S3-S1.
可得 aq3=aq+aq2.
化简得 q2-q-1=0.
解得 q=1 ± 5
2 .
(2)证明:若 q=1,则{an}的每项 an=a,此时 am+k,an+k,al+k 显然构成等差数列.
若 q≠1,由 Sm,Sn,Sl 构成等差数列可得 Sm+Sl=2Sn,即
a(qm-1)
q-1 +a(ql-1)
q-1 =2a(qn-1)
q-1 .
整理得 qm+ql=2qn.
因此,am+k+al+k=aqk-1(qm+ql)=2aqn+k-1=2an+k.
所以,am+k,an+k,al+k 成等差数列.
大纲理数 20.D5[2011·四川卷] 设 d 为非零实数,an=1
n[C1nd+2C2nd2+…+(n-1)Cn-1n dn-1
+nCnndn](n∈N*).
(1)写出 a1,a2,a3 并判断{an}是否为等比数列.若是,给出证明;若不是,说明理由;
(2)设 bn=ndan(n∈N*),求数列{bn}的前 n 项和 Sn.
大纲理数 20.D5[2011·四川卷] 【解答】 (1)由已知可得 a 1=d,a2=d(1+d),a3=d(1+
d)2.
当 n≥2,k≥1 时,k
nCkn=Ck-1n-1,因此
由此可见,当 d≠-1 时,{an}是以 d 为首项,d+1 为公比的等比数列;
当 d=-1 时,a1=-1,an=0(n≥2),此时{an}不是等比数列.
(2)由(1)可知,an=d(d+1)n-1,从而 bn=nd2(d+1)n-1,
Sn=d2[1+2(d+1)+3(d+1)2+…+(n-1)(d+1)n-2+n(d+1)n-1]. ①
当 d=-1 时,Sn=d2=1.
当 d≠-1 时,①式两边同乘 d+1 得
(d+1)Sn=d2[(d+1)+2(d+1)2+…+(n-1)(d+1)n-1+n(d+1)n].②
①,②式相减可得
-dSn=d2[1+(d+1)+(d+1)2+…+(d+1)n-1-n(d+1)n]
=d2[(d+1)n-1
d -n(d+1)n].
化简即得 Sn=(d+1)n(nd-1)+1.
综上,Sn=(d+1)n(nd-1)+1.
课标理数 20.D5[2011·天津卷] 已知数列{a n}与{bn}满足 bnan+an+1+bn+1an+2=0,bn=
3+(-1)n
2 ,n∈N*,且 a1=2,a2=4.
(1)求 a3,a4,a5 的值;
(2)设 cn=a2n-1+a2n+1,n∈N*,证明{cn}是等比数列;
(3)设 Sk=a2+a4+…+a2k,k∈N*,证明∑
4n
Sk
ak<7
6(n∈N*).
课标理数 20.D5[2011·天津卷] 【解答】 (1)由 b n=3+(-1)n
2 ,n∈N *,可得 bn=
{1,n为奇数,
2,n为偶数.
又 bnan+an+1+bn+1an+2=0,
当 n=1 时,a1+a2+2a3=0,
由 a1=2,a2=4,可得 a3=-3;
当 n=2 时,2a2+a3+a4=0,可得 a4=-5;
当 n=3 时,a3+a4+2a5=0,可得 a5=4.
(2)证明:对任意 n∈N*,
a2n-1+a2n+2a2n+1=0,①
2a2n+a2n+1+a2n+2=0,②
a2n+1+a2n+2+2a2n+3=0.③
②-③,得 a2n=a2n+3.④
将④代入①,可得 a2n+1+a2n+3=-(a2n-1+a2n+1),
即 cn+1=-cn(n∈N*).
又 c1=a1+a3=-1,故 cn≠0,因此cn+1
cn =-1.
所以{cn}是等比数列.
(3)证明:由(2)可得 a2k-1+a2k+1=(-1)k.于是,对任意 k∈N*且 k≥2,有 a1+a3=-1,-
(a3+a5)=-1,a5+a7=-1,…,(-1)k(a2k-3+a2k-1)=-1.
将以上各式相加,得 a1+(-1)ka2k-1=-(k-1),
即 a2k-1=(-1)k+1(k+1),此式当 k=1 时也成立.
由④式得 a2k=(-1)k+1(k+3).
从而 S2k=(a2+a4)+(a6+a8)+…+(a4k-2+a4k)=-k,S2k-1=S2k-a4k=k+3.
所以,对任意 n∈N*,n≥2,
4n
∑
k=1
Sk
ak=
n
∑
m=1 (S4m-3
a4m-3+S4m-2
a4m-2+S4m-1
a4m-1+S4m
a4m)
=
n
∑
m=1 (2m+2
2m -2m-1
2m+2-2m+3
2m+1+ 2m
2m+3)
=
n
∑
m=1 ( 2
2m(2m+1)+ 3
(2m+2)(2m+3))
= 2
2 × 3+
n
∑
m=2
5
2m(2m+1)+ 3
(2n+2)(2n+3)
<1
3+
n
∑
m=2
5
(2m-1)(2m+1)+ 3
(2n+2)(2n+3)
=1
3+5
2·(1
3-1
5 )+(1
5-1
7 )+…+( 1
2n-1- 1
2n+1)+ 3
(2n+2)(2n+3)
=1
3+5
6-5
2· 1
2n+1+ 3
(2n+2)(2n+3)<7
6.
对于 n=1,不等式显然成立.
课标文数 20.D5[2011·天津卷] 已知数列{an}与{bn}满足 bn+1an+bnan+1=(-2)n+1,bn=
3+(-1)n-1
2 ,n∈N*,且 a1=2.
(1)求 a2,a3 的值;
(2)设 cn=a2n+1-a2n-1,n∈N*,证明{cn}是等比数列;
(3)设 Sn 为{an}的前 n 项和,证明S1
a1+S2
a2+…+S2n-1
a2n-1+S2n
a2n≤n-1
3(n∈N*).
课标文数 20.D5[2011·天津卷] 【解答】 (1)由 bn=3+(-1)n-1
2 ,n∈N,
可得 bn={2,n为奇数,
1,n为偶数.
又 bn+1an+bnan+1=(-2)n+1,
当 n=1 时,a1+2a2=-1,由 a1=2,可得 a2=-3
2;
当 n=2 时,2a2+a3=5,可得 a3=8.
(2)证明:对任意 n∈N*,
a2n-1+2a2n=-22n-1+1,①
2a2n+a2n+1=22n+1.②
②-①,得 a2n+1-a2n-1=3×22n-1,即 cn=3×22n-1.
于是cn+1
cn =4.
所以{cn}是等比数列.
(3)证明:a1=2,由(2)知,当 k∈N*且 k≥2 时,
a2k-1=a1+(a3-a1)+(a5-a3)+(a7-a5)+…+(a2k-1-a2k-3)
=2+3(2+23+25+…+22k-3)=2+3×2(1-4k-1)
1-4 =22k-1,
故对任意 k∈N*,a2k-1=22k-1.
由①得 22k-1+2a2k=-22k-1+1,
所以 a2k=1
2-22k-1,k∈N*.
因此,S2k=(a1+a2)+(a3+a4)+…+(a2k-1+a2k)=k
2.
于是,S2k-1=S2k-a2k=k-1
2 +22k-1.
故S2k-1
a2k-1+S2k
a2k=
k-1
2 +22k-1
22k-1 +
k
2
1
2-22k-1
=k-1+22k
22k - k
22k-1=1-1
4k- k
4k(4k-1).
所以,对任意 n∈N*,
S1
a1+S2
a2+…+S2n-1
a2n-1+S2n
a2n
=(S1
a1+S2
a2)+(S3
a3+S4
a4)+…+(S2n-1
a2n-1+S2n
a2n)
=(1-1
4- 1
12)+(1- 1
42- 2
42(42-1))+…+1- 1
4n- n
4n(4n-1)
=n-(1
4+ 1
12)-( 1
42+ 2
42(42-1))-…- 1
4n+ n
4n(4n-1)≤n-(1
4+ 1
12)=n-1
3.
课标文数 19.D5[2011·浙江卷] 已知公差不为 0 的等差数列{an}的首项 a1 为 a(a∈R),且 1
a1,
1
a2, 1
a4成等比数列.
(1)求数列{an}的通项公式;
(2)对 n∈N*,试比较 1
a2+ 1
a22+…+ 1
a2n与 1
a1的大小.
课标文数 19.D5[2011·浙江卷] 【解答】 设等差数列{an}的公差为 d,由题意可知( 1
a2 )
2
= 1
a1· 1
a4,
即(a1+d)2=a1(a1+3d),从而 a1d=d2.
因为 d≠0,所以 d=a1=a,
故通项公式 an=na.
(2)记 Tn= 1
a2+ 1
a22+…+ 1
a2n.因为 a2n=2na,
所以 Tn=1
a(1
2+ 1
22+…+ 1
2n)=1
a·
1
2[1-(1
2 )n
]
1-1
2
=1
a[1-(1
2 )n
].
从而,当 a>0 时,Tn< 1
a1,当 a<0 时,Tn> 1
a1.
大纲理数 21.D5[2011·重庆卷] 设实数数列{a n}的前 n 项和 Sn 满足 Sn+1 =an+1 Sn(n∈
N*).
(1)若 a1,S2,-2a2 成等比数列,求 S2 和 a3;
(2)求证:对 k≥3 有 0≤ak+1≤ak≤4
3.
大纲理数 21.D5[2011·重庆卷] 【解答】 (1)由题意{S=-2a1a2,
S2=a2S1=a1a2,得 S22=-2S2,
由 S2 是等比中项知 S2≠0.因此 S2=-2.
由 S2+a3=S3=a3S2 解得
a3= S2
S2-1=
-2
-2-1=2
3.
(2)证法一:由题设条件有 Sn+an+1=an+1Sn,
故 Sn≠1,an+1≠1 且 an+1= Sn
Sn-1,Sn= an+1
an+1-1,
从而对 k≥3 有
ak= Sk-1
Sk-1-1= ak-1+Sk-2
ak-1+Sk-2-1=
ak-1+ ak-1
ak-1-1
ak-1+ ak-1
ak-1-1-1
= a
a-ak-1+1.①
因 a 2k-1-ak-1+1=(ak-1-1
2)2
+3
4>0 且 a 2k-1≥0,由①得 ak≥0.
要证 ak≤4
3,由①只要证 a
a-ak-1+1≤4
3,
即证 3a 2k-1≤4(a 2k-1-ak-1+1),即(ak-1-2)2≥0,此式明显成立.
因此 ak≤4
3(k≥3).
最后证 ak+1≤ak,若不然 ak+1= a
a-ak+1>ak,
又因 ak≥0,故 ak
a-ak+1>1,即(ak-1)2<0.矛盾.
因此 ak+1≤ak(k≥3).
证法二:由题设知 Sn+1=Sn+an+1=an+1Sn,
故方程 x2-Sn+1x+Sn+1=0 有根 Sn 和 an+1(可能相同).
因此判别式 Δ=S 2n+1-4Sn+1≥0.
又由 Sn+2=Sn+1+an+2=an+2Sn+1 得 an+2≠1 且 Sn+1= an+2
an+2-1.
因此 a
(an+2-1)2- 4an+2
an+2-1≥0,即 3a 2n+2-4an+2≤0,
解得 0≤an+2≤4
3.
因此 0≤ak≤4
3(k≥3).
由 ak= Sk-1
Sk-1-1≥0(k≥3),得
ak+1-ak= Sk
Sk-1-ak
=ak( Sk-1
akSk-1-1-1)=ak( Sk-1
S
Sk-1-1-1
-1)
=- ak
S-Sk-1+1=- ak
(Sk-1-1
2)2
+3
4
≤0,
因此 ak+1≤ak(k≥3).