2014重庆（理科数学）高考试题

2014重庆（理科数学）高考试题

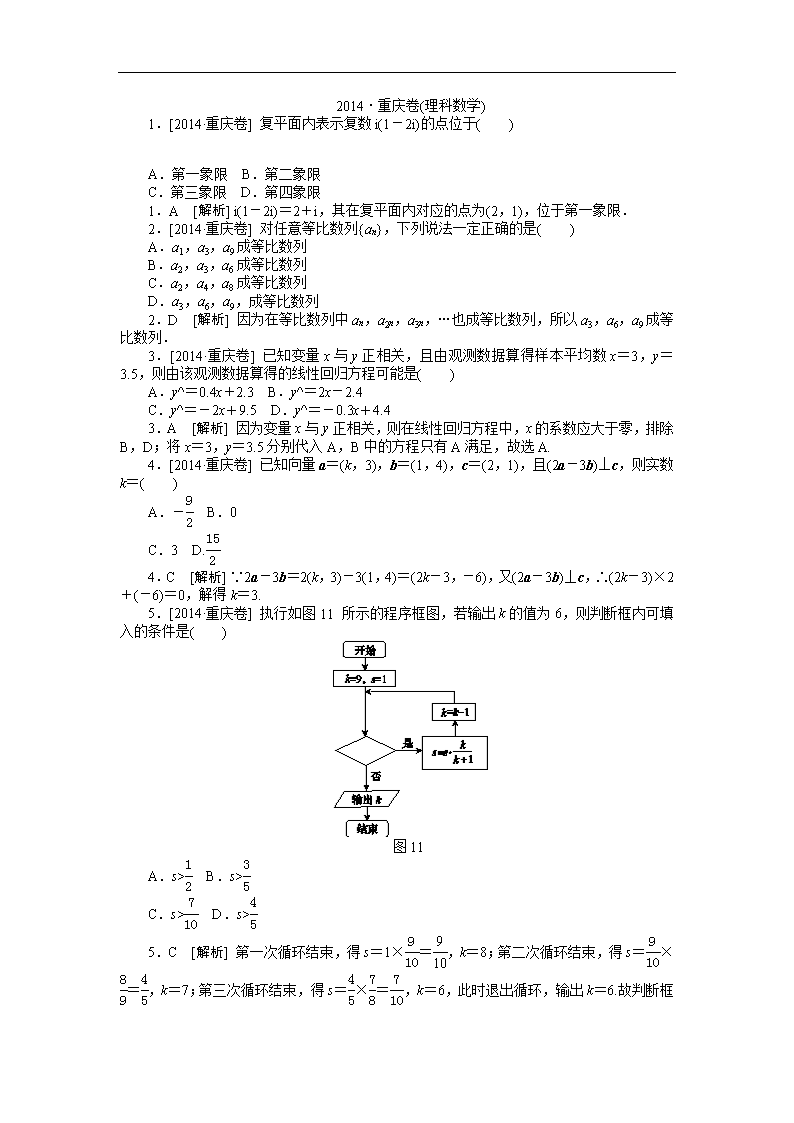
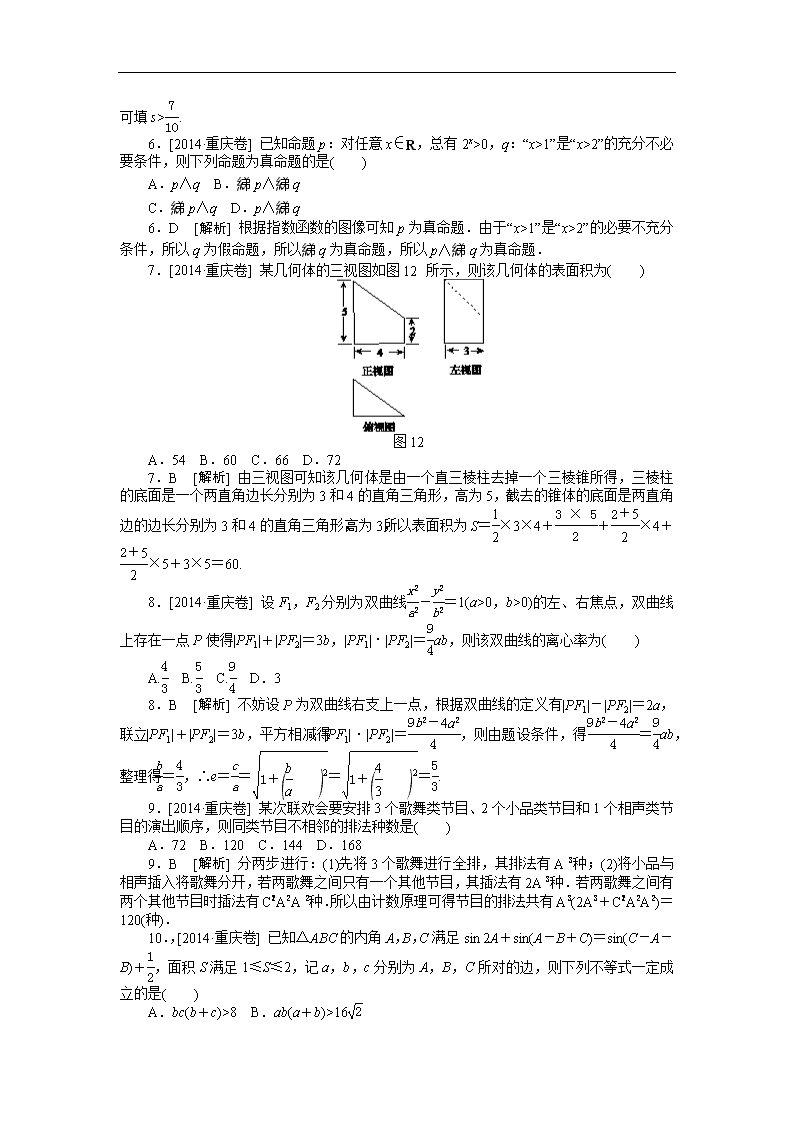
‎2014·重庆卷(理科数学)‎ ‎1．[2014·重庆卷] 复平面内表示复数i(1－2i)的点位于(　　)‎ ‎　 　　　　　 　　　　　 　　　　‎ A．第一象限 B．第二象限 ‎ C．第三象限 D．第四象限 ‎1．A　[解析] i(1－2i)＝2＋i，其在复平面内对应的点为(2，1)，位于第一象限．‎ ‎2．[2014·重庆卷] 对任意等比数列{an}，下列说法一定正确的是(　　)‎ A．a1，a3，a9成等比数列 ‎ B．a2，a3，a6成等比数列 ‎ C．a2，a4，a8成等比数列 ‎ D．a3，a6，a9，成等比数列 ‎2．D　[解析] 因为在等比数列中an，a2n，a3n，…也成等比数列，所以a3，a6，a9成等比数列．‎ ‎3．[2014·重庆卷] 已知变量x与y正相关，且由观测数据算得样本平均数x＝3，y＝3.5，则由该观测数据算得的线性回归方程可能是(　　)‎ A．y^＝0.4x＋2.3 B．y^＝2x－2.4‎ C．y^＝－2x＋9.5 D．y^＝－0.3x＋4.4‎ ‎3．A　[解析] 因为变量x与y正相关，则在线性回归方程中，x的系数应大于零，排除B，D；将x＝3，y＝3.5分别代入A，B中的方程只有A满足，故选A.‎ ‎4．[2014·重庆卷] 已知向量a＝(k，3)，b＝(1，4)，c＝(2，1)，且(2a－3b)⊥c，则实数k＝(　　)‎ A．－ B．0‎ C．3 D. ‎4．C　[解析] ∵2a－3b＝2(k，3)－3(1，4)＝(2k－3，－6)，又(2a－3b)⊥c，∴(2k－3)×2＋(－6)＝0，解得k＝3.‎ ‎5．[2014·重庆卷] 执行如图11所示的程序框图，若输出k的值为6，则判断框内可填入的条件是(　　)‎ 图11　　　‎ A．s> B．s> ‎ C．s> D．s> ‎5．C　[解析] 第一次循环结束，得s＝1×＝，k＝8；第二次循环结束，得s＝×＝，k＝7；第三次循环结束，得s＝×＝，k＝6，此时退出循环，输出k＝6.故判断框内可填s>.‎ ‎6．[2014·重庆卷] 已知命题p：对任意x∈R，总有2x>0，q：“x>1”是“x>2”的充分不必要条件，则下列命题为真命题的是(　　)‎ A．p∧q B．綈p∧綈q ‎ C．綈p∧q D．p∧綈q ‎6．D　[解析] 根据指数函数的图像可知p为真命题．由于“x>1”是“x>2”的必要不充分条件，所以q为假命题，所以綈q为真命题，所以p∧綈q为真命题．‎ ‎7．[2014·重庆卷] 某几何体的三视图如图12所示，则该几何体的表面积为(　　)‎ 图12‎ A．54 B．60 C．66 D．72‎ ‎7．B　[解析] 由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥所得，三棱柱的底面是一个两直角边长分别为3和4的直角三角形，高为5，截去的锥体的底面是两直角边的边长分别为3和4的直角三角形，高为3，所以表面积为S＝×3×4＋＋×4＋×5＋3×5＝60.‎ ‎8．[2014·重庆卷] 设F1，F2分别为双曲线－＝1(a>0，b>0)的左、右焦点，双曲线上存在一点P使得|PF1|＋|PF2|＝3b，|PF1|·|PF2|＝ab，则该双曲线的离心率为(　　)‎ A. B. C. D．3‎ ‎8．B　[解析] 不妨设P为双曲线右支上一点，根据双曲线的定义有|PF1|－|PF2|＝2a，联立|PF1|＋|PF2|＝3b，平方相减得|PF1|·|PF2|＝，则由题设条件，得＝ab，整理得＝，∴e＝＝＝＝.‎ ‎9．[2014·重庆卷] 某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法种数是(　　)‎ A．72 B．120 C．144 D．168‎ ‎9．B　[解析] 分两步进行：(1)先将3个歌舞进行全排，其排法有A种；(2)将小品与相声插入将歌舞分开，若两歌舞之间只有一个其他节目，其插法有2A种．若两歌舞之间有两个其他节目时插法有CAA种．所以由计数原理可得节目的排法共有A(2A＋CAA)＝120(种)．‎ ‎10．，[2014·重庆卷] 已知△ABC的内角A，B，C满足sin 2A＋sin(A－B＋C)＝sin(C－A－B)＋，面积S满足1≤S≤2，记a，b，c分别为A，B，C所对的边，则下列不等式一定成立的是(　　)‎ A．bc(b＋c)>8 B．ab(a＋b)>16 ‎ C．6≤abc≤12 D．12≤abc≤24‎ ‎10．A　[解析] 因为A＋B＋C＝π，所以A＋C＝π－B，C＝π－(A＋B)，所以由已知等式可得sin 2A＋sin(π－2B)＝sin[π－2(A＋B)]＋，即sin 2A＋sin 2B＝sin 2(A＋B)＋，‎ 所以sin[(A＋B)＋(A－B)]＋sin[(A＋B)－(A－B)]＝sin 2(A＋B)＋，‎ 所以2 sin(A＋B)cos(A－B)＝2sin(A＋B)cos(A＋B)＋， ‎ 所以2sin(A＋B)[cos(A－B)－cos(A＋B)]＝，所以sin Asin Bsin C＝.‎ 由1≤S≤2，得1≤bcsin A≤2.由正弦定理得a＝2Rsin A，b＝2Rsin B，c＝2Rsin C，所以1≤2R2·sin Asin Bsin C≤2，所以1≤≤2，即2≤R≤2　，所以bc(b＋c)>abc＝8R3sin Asin Bsin C＝R3≥8.‎ ‎11．[2014·重庆卷] 设全集U＝{n∈N|1≤n≤10}，A＝{1，2，3，5，8}，B＝{1，3，5，7，9}，则(∁UA)∩B＝________．‎ ‎11．{7，9}　[解析] 由题知∁UA＝{4，6，7，9，10}，‎ ‎∴(∁UA)∩B＝{7，9}．‎ ‎12．[2014·重庆卷] 函数f(x)＝log2·log(2x)的最小值为________．‎ ‎12．－　[解析] f(x)＝log2 ·log(2x)＝log2 x·2log2(2x)＝log2x·(1＋log2x)＝(log2x)2＋log2x＝－，所以当x＝时，函数f(x)取得最小值－.‎ ‎13．[2014·重庆卷] 已知直线ax＋y－2＝0与圆心为C的圆(x－1)2＋(y－a)2＝4相交于A，B两点，且△ABC为等边三角形，则实数a＝________．‎ ‎13．4±　[解析] 由题意可知圆的圆心为C(1，a)，半径r＝2，则圆心C到直线ax＋y－2＝0的距离d＝＝.∵△ABC为等边三角形，∴|AB|＝r＝2.又|AB|＝2，∴2＝2，即a2－8a＋1＝0，解得a＝4±.‎ ‎14．[2014·重庆卷] 过圆外一点P作圆的切线PA(A为切点)，再作割线PBC依次交圆于B，C.若PA＝6，AC＝8，BC＝9，则AB＝________．‎ ‎14．4　[解析] 根据题意，作出图形如图所示，由切割线定理，得PA2＝PB·PC＝PB·(PB＋BC)，即36＝PB·(PB＋9)∴PB＝3，∴PC＝12.由弦切角定理知∠PAB＝∠PCA，又∠APB＝∠CPA，∴△PAB∽△PCA，∴＝，即AB＝＝＝4.‎ ‎15．[2014·重庆卷] 已知直线l的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ－4cos θ＝0(ρ≥0，0≤θ<2π)，则直线l与曲线C的公共点的极径ρ＝________．‎ ‎15. 　[解析] 由题意，得直线l的普通方程为x－y＋1＝0，曲线C的平面直角坐标方程为y2＝4x，联立直线l与曲线C的方程，解得所以直线l与曲线C的公共点的极径ρ＝＝.‎ ‎16．[2014·重庆卷] 若不等式|2x－1|＋|x＋2|≥a2＋a＋2对任意实数x恒成立，则实数a的取值范围是________．‎ ‎16.　[解析] 令f(x)＝|2x－1|＋|x＋2|，则①当x<－2时，f(x)＝－2x＋1－x－2＝－3‎ x－1>5；②当－2≤x≤时，f(x)＝－2x＋1＋x＋2＝－x＋3，故≤f(x)≤5；③当x>时，f(x)＝2x－1＋x＋2＝3x＋1>.综合①②③可知f(x)≥，所以要使不等式恒成立，则需a2＋a＋2≤，解得－1≤a≤.‎ ‎17．，，[2014·重庆卷] 已知函数f(x)＝sin(ωx＋φ)的图像关于直线x＝对称，且图像上相邻两个最高点的距离为π.‎ ‎(1)求ω和φ的值；‎ ‎(2)若f＝，求cos的值．‎ ‎17．解：(1)因为f(x)的图像上相邻两个最高点的距离为π，所以ƒ(x)的最小正周期T＝π，从而ω＝＝2.‎ 又因为f(x)的图像关于直线x＝对称，‎ 所以2×＋φ＝kπ＋，k＝0，±1，±2，….‎ 因为－≤φ＜，‎ 所以φ＝－.‎ ‎(2)由(1)得ƒ＝sin(2×－)＝，‎ 所以sin＝.‎ 由＜α＜得0＜α－＜，‎ 所以cos＝＝＝.‎ 因此cos ‎＝sin α ‎＝sin ‎＝sincos＋cossin ‎＝×＋× ‎＝.‎ ‎18．，[2014·重庆卷] 一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3.从盒中任取3张卡片．‎ ‎(1)求所取3张卡片上的数字完全相同的概率；‎ ‎(2)X表示所取3张卡片上的数字的中位数，求X的分布列与数学期望．‎ ‎(注：若三个数a，b，c满足a≤b≤c，则称b为这三个数的中位数)‎ ‎18．解：(1)由古典概型中的概率计算公式知所求概率为P＝＝.‎ ‎(2)X的所有可能值为1，2，3，且 P(X＝1)＝＝，‎ P(X＝2)＝＝，‎ P(X＝3)＝＝，‎ 故X的分布列为 X ‎1‎ ‎2‎ ‎3‎ P 从而E(X)＝1×＋2×＋3×＝.‎ ‎19．，[2014·重庆卷]如图13所示，四棱锥PABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB＝2，∠BAD＝，M为BC上一点，且BM＝，MP⊥AP.‎ ‎(1)求PO的长；‎ ‎(2)求二面角APMC的正弦值．‎ 图13‎ ‎19．解：(1)如图所示，连接AC，BD，因为四边形ABCD为菱形，所以AC∩ BD＝O，且AC⊥BD.以O为坐标原点，，，的方向分别为x轴，y轴，z轴的正方向建立空间直角坐标系O xyz.‎ 因为∠BAD＝，‎ 所以OA＝AB·cos＝，OB＝AB·sin＝1，‎ 所以O(0，0，0)，A(，0，0)，B(0，1，0)，C(－，0，0)，＝(0，1，0)，＝(－，－1，0)．‎ 由BM＝，BC＝2知，＝＝，‎ 从而＝＋＝，‎ 即M.‎ 设P(0，0，a)，a＞0，则＝(－，0，a)，＝.因为MP⊥AP，所以·＝0，即－＋a2＝0，所以a＝或a＝－(舍去)，即PO＝.‎ ‎(2)由(1)知，＝，＝，＝.设平面APM的法向量为n ‎1＝(x1，y1，z1)，平面PMC的法向量为n2＝(x2，y2，z2)．‎ 由n1·＝0, n1·＝0，得 故可取n1＝.‎ 由n2·＝0，n2·＝0，得 故可取n2＝(1，－，－2)．‎ 从而法向量n1，n2的夹角的余弦值为 cos〈n1，n2〉＝＝－，‎ 故所求二面角APMC的正弦值为.‎ ‎20．[2014·重庆卷] 已知函数f(x)＝ae2x－be－2x－cx(a，b，c∈R)的导函数f′(x)为偶函数，且曲线y＝f(x)在点(0，f(0))处的切线的斜率为4－c.‎ ‎(1)确定a，b的值；‎ ‎(2)若c＝3，判断f(x)的单调性；‎ ‎(3)若f(x)有极值，求c的取值范围．‎ ‎20．解：(1)对f(x)求导得f′(x)＝2ae2x＋2be－2x－c，由f′(x)为偶函数，知f′(－x)＝f′(x)，即2(a－b)(e2x－e－2x)＝0.因为上式总成立，所以a＝b.‎ 又f′(0)＝2a＋2b－c＝4－c，所以a＝1，b＝1.‎ ‎(2)当c＝3时，f(x)＝e2x－e－2x－3x，那么 f′(x)＝2e2x＋2e－2x－3≥2－3＝1>0，‎ 故f(x)在R上为增函数．‎ ‎(3)由(1)知f′(x)＝2e2x＋2e－2x－c，而2e2x＋2e－2x≥2＝4，当且仅当x＝0时等号成立．‎ 下面分三种情况进行讨论：‎ 当c<4时，对任意x∈R，f′(x)＝2e2x＋2e－2x－c>0，此时f(x)无极值．‎ 当c＝4时，对任意x≠0，f′(x)＝2e2x＋2e－2x－4>0，此时f(x)无极值．‎ 当c>4时，令e2x＝t，注意到方程2t＋－c＝0有两根t1，2＝>0，则f′(x)＝0有两个根x1＝ln t1，x2＝ln t2.‎ 当x1x2时，f′(x)>0.‎ 从而f(x)在x＝x2处取得极小值．‎ 综上，若f(x)有极值，则c的取值范围为(4，＋∞)．‎ ‎21．，[2014·重庆卷] 如图14所示，设椭圆＋＝1(a>b>0)的左、右焦点分别为F1，F2，点D在椭圆上，DF1⊥F1F2，＝2，△DF1F2的面积为.‎ ‎(1)求椭圆的标准方程；‎ ‎(2)设圆心在y轴上的圆与椭圆在x轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径．‎ 图14‎ ‎21．解：(1)设F1(－c，0)，F2(c，0)，其中c2＝a2－b2.‎ 由＝2得|DF1|＝＝c.‎ 从而S△DF1F2＝|DF1||F1F2|＝c2＝，故c＝1.‎ 从而|DF1|＝，由DF1⊥F1F2得|DF2|2＝|DF1|2＋|F1F2|2＝，因此|DF2|＝，‎ 所以2a＝|DF1|＋|DF2|＝2，故a＝，b2＝a2－c2＝1.‎ 因此，所求椭圆的标准方程为＋y2＝1.‎ ‎(2)如图所示，设圆心在y轴上的圆C与椭圆＋y2＝1相交，P1(x1，y1)，P2(x2，y2)是两个交点，y1>0，y2>0，F1P1，F2P2是圆C的切线，且F1P1⊥F2P2.由圆和椭圆的对称性，易知，x2＝－x1，y1＝y2，|P1P2|＝2|x1|.‎ 由(1)知F1(－1，0)，F2(1，0)，所以＝(x1＋1，y1)，＝(－x1－1，y1)．再由F1P1⊥F2P2得－(x1＋1)2＋y＝0.由椭圆方程得1－＝(x1＋1)2，即3x＋4x1＝0，解得x1＝－或x1＝0.‎ 当x1＝0时，P1，P2重合，此时题设要求的圆不存在．‎ 当x1＝－时，过P1，P2分别与F1P1，F2P2垂直的直线的交点即为圆心C.‎ 由F1P1，F2P2是圆C的切线，且F1P1⊥F2P2，知CP1⊥CP2.又|CP1|＝|CP2|，故圆C的半径|CP1|＝|P1P2|＝|x1|＝.‎ ‎22．，，[2014·重庆卷] 设a1＝1，an＋1＝＋b(n∈N*)．‎ ‎(1)若b＝1，求a2，a3及数列{an}的通项公式．‎ ‎(2)若b＝－1，问：是否存在实数c使得a2nf(a2k＋1)>f(1)＝a2，即 ‎1>c>a2k＋2>a2.‎ 再由f(x)在(－∞，1]上为减函数，得c＝f(c)f(a2k＋1)＝a2k＋2，‎ a2(k＋1)＝f(a2k＋1)f(a2n＋1)，即a2n＋1>a2n＋2.‎ 所以a2n＋1>－1，解得a2n＋1>.　④‎ 综上，由②③④知存在c＝使a2n

查看更多