- 2021-06-30 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学(理)卷·2018届陕西省西安市一中高二上学期期末考试(2017-01)
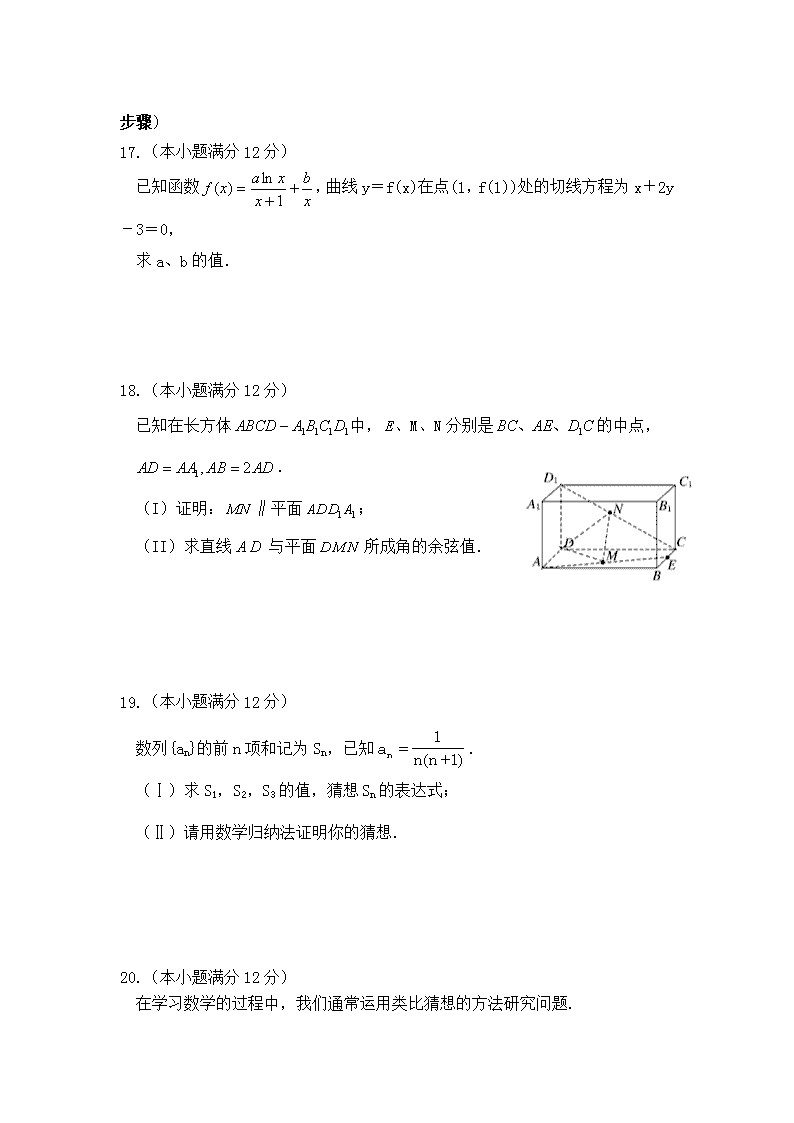
2016—2017学年度第二学期期末考试 高二数学试题(理科) 命题人:白恒兴 一、选择题:(本大题共12小题,每小题3分,共36分) 1.命题“设a、b、c∈R,若ac2>bc2,则a>b”的逆命题、否命题、逆否命题中真命题共有( ) A.0个 B.1个 C.2个 D.3个 2.“”是“”的什么条件?( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件 3.命题“对任意,都有”的否定为( ) A.对任意,都有 B.不存在,都有 C.存在,使得 D.存在,使得 4.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px的通径为4, 则P=( ) A.1 B.4 C.2 D.8 5.已知数列、、、、、…根据前三项给出的规律,则实数对 (2a,2b)可能是( ) A.(,﹣) B.(19,﹣3) C.(,) D.(19,3) 6.已知21×1=2,22×1×3=3×4,23×1×3×5=4×5×6,…,以此类推,第5个等式为( ) A.24×1×3×5×7=5×6×7×8 B.25×1×3×5×7×9=5×6×7×8×9 C.24×1×3×5×7×9=6×7×8×9×10 D.25×1×3×5×7×9=6×7×8×9×10 7.用反证法证明“三角形中最多只有一个内角是钝角”的结论的否定是( ) A.有两个内角是钝角 B.有三个内角是钝角 C.至少有两个内角是钝角 D.没有一个内角是钝角 8.已知曲线上一点,则点A处的切线斜率为 ( ) A.2 B.4 C.6 D.8 9.曲线y=e2x在点(0,1)处的切线方程为( ) A.y=x+1 B.y=﹣2x+1 C.y=2x﹣1 D.y=2x+1 10.设函数若则等于( ) A.2 B.-2 C.3 D.-3 11.已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…, fn(x)=fn﹣1′(x),则f2015(x)等于( ) A.sinx B.﹣sinx C.cosx D.﹣cosx 12.函数的图像在点处的切线的倾斜角为( ) A. B.0 C. D.l 二、填空题(本大题共4小题,每小题4分,共16分) 13.已知向量=(0,2,1),=(﹣1,1,﹣2),则与的夹角的大小为 ____. 14.比较大小:(填不等号). 15.函数f(x)=xex的导函数f′(x)= ____ . 16.若函数f(x)=3sinx﹣4cosx,则f′()= ____ . 三、解答题(每小题 12分,共48分;解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分) 已知函数,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0, 求a、b的值. 18.(本小题满分12分) 已知在长方体中,分别是的中点, . (I)证明:∥平面; (II)求直线与平面所成角的余弦值. 19.(本小题满分12分) 数列{an}的前n项和记为Sn,已知. (Ⅰ)求S1,S2,S3的值,猜想Sn的表达式; (Ⅱ)请用数学归纳法证明你的猜想. 20.(本小题满分12分) 在学习数学的过程中,我们通常运用类比猜想的方法研究问题. (1)在圆中,AB为圆的任意一条直径,C为圆上异于A、B的任意一点,当直线AC与BC的斜率、存在时,求的值; (2)在椭圆中,AB为过椭圆中心的任意一条弦,C为椭圆上异于A、B的任意一点,当直线AC与BC的斜率、存在时,求的值; (3)直接写出椭圆中类似的结论(不用证明). 市一中大学区 2016—2017学年度第二学期期末考试 高二理科数学答案 一、选择题(每小题3分,共36分) 1.B 2.A 3.D 4.C 5.D 6.D 7.C. 8.D. 9.D 10.C. 11.D 12.A 二、填空题(每小题4分,共16分) 13. 14. > 15.(1+x)ex 16. 4 三、解答题(共48分) 17.(本题满分12分) 18.(本题满分12分) 解析:(I)方法一:(面面平行)取DC的中点O,连接ON,OM,证明平面MON//平面ADD1A1即可. 方法二:(坐标法)如图,建立空间直角坐标系,设AD=1,则AB=2 平面,就是平面的一个法向量 ,,,又, 平面,平面………….5分 (II)设平面DMN的一个法向量为,,, ,,令,则,, ,所以直线DA与平面所成角的正弦值是…..12分 19.(本题满分12分) 20.(本题满分12分)(1)=-1……..4分; (2)设,,则,=,又由, ,两式相减得,所以=……9分 (3)=-………12分.查看更多