2015年高考试题——数学理（重庆卷）原卷版

2015年高考试题——数学理（重庆卷）原卷版

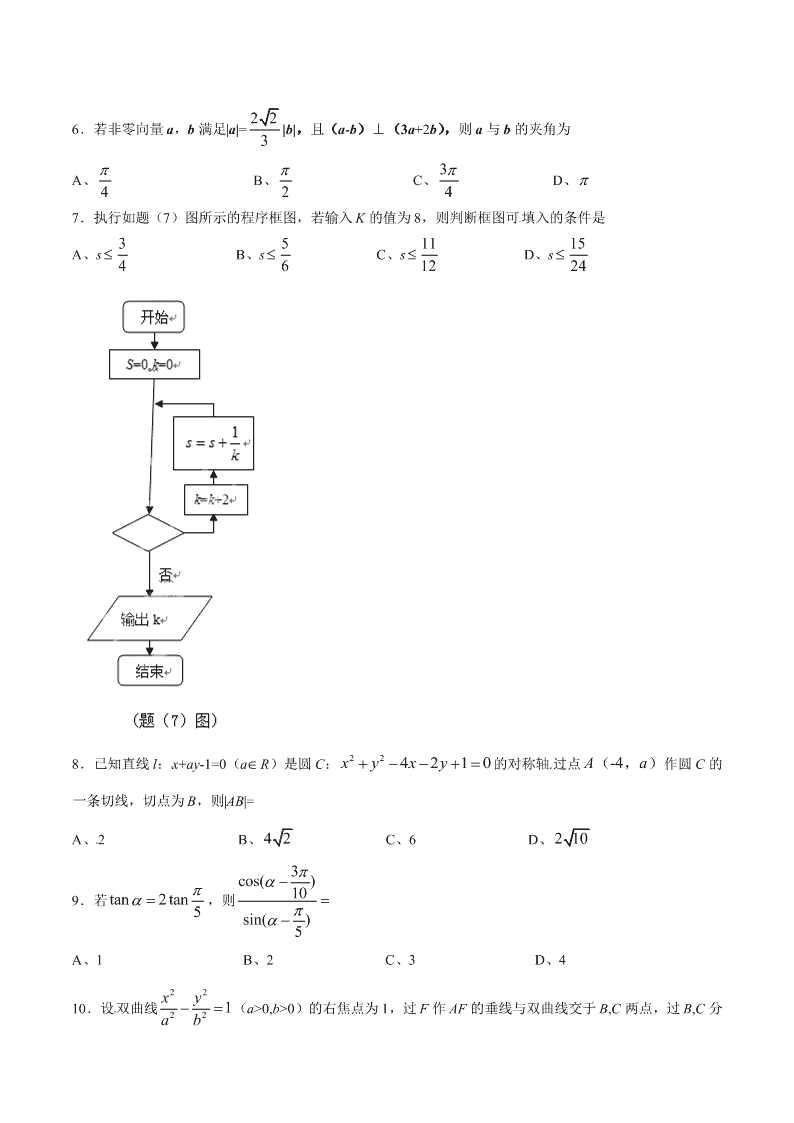
本试卷包括选择题、填空题和解答题三部分，共 6 页，时量 120 分钟，满分 150 分. 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1．已知集合 A= 1,2,3 ,B= 2,3 ，则 A、A=B B、A B= C、AØ B D、BØ A 2．在等差数列 na 中，若 2a =4， 4a =2，则 6a = A、-1 B、0 C、1 D、6 3．重庆市 2013 年各月的平均气温（ oC ）数据的茎叶图如下： 0 8 9 1 2 5 8 2 0 0 3 3 8 3 1 2 [来源:学#科#网] 则这组数据的中位数是 A、19 B、20 C、21.5 D、23 4．“ 1x  ”是“ 1 2 log ( 2) 0x ”的 A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件 5．某几何体的三视图如图所示，则该几何体的体积为 A、 1 3  B、 2 3  C、 1 23  D、 2 23  6．若非零向量 a，b 满足|a|= 22 3 |b|，且（a-b）  （3a+2b）， 则 a 与 b 的夹角为 A、 4  B、 2  C、 3 4  D、 7．执行如题（7）图所示的程序框图，若输入 K 的值为 8，则判断框图可填入的条件是 A、s 3 4 B、s 5 6 C、s 11 12 D、s  15 24 8．已知直线 l：x+ay-1=0（aR）是圆 C： 224 2 1 0x y x y     的对称轴.过点 A（-4，a）作圆 C 的 一条切线，切点为 B，则|AB|= A、2 B、 42 C、6 D、 2 10 9．若 tan 2tan 5   ，则 3cos( )10 sin( )5      A、1 B、2 C、3 D、4 10．设双曲线 22 221xy ab（a>0,b>0）的右焦点为 1，过 F 作 AF 的垂线与双曲线交于 B,C 两点，过 B,C 分 别作 AC，AB 的垂线交于点 D.若 D 到直线 BC 的距离小于 22a a b，则该双曲线的渐近线斜率的取值 范围是[来源:学_科_网 Z_X_X_K] A、（-1,0） （0,1） B、（-  ，-1） （1，+  ） C、（- 2 ，0） （0， 2 ） D、（- ，- 2 ） （ 2 ，+ ） 二、填空题：本大题共 6小题，考生作答 5 小题，每小题 5 分，共 25 分.把答案填写在答题卡 相应位置上. 1 1．设复数 a+bi（a，bR）的模为 3 ，则（a+bi）（ a-bi）=________. 12． 5 3 1 2 x x  的展开式中 8x 的系数是________(用数字作答). 13．在 ABC 中，B=120o ，AB= 2 ，A 的角平分线 AD= 3 ,则 AC=_______. 考生注意：（14）、（ 15）、（ 16）三题为选做题，请从中任选两题作答，若三题全做，则按前两题给分. 14．如图，圆 O 的弦 AB，CD 相交于点 E，过点 A 作圆 O 的切线与 DC 的延长线交于点 P，若 PA=6，AE=9， PC=3，CE:ED=2:1，则 BE=_______. 15．已知直线 l 的参数方程为 1 1 xt yt      （t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立坐标系， 曲线 C 的极坐标方程为 2 35cos2 4( 0, )44        ，则直线 l 与曲线 C 的交点的极坐标为_______. 16．若函数 f（x） 12x x a    的最小值为 5，则实数 a=_______. 三、解答题：本大题共 6 小题，共 75 分，解答应写出文字说明、证明过程或演算步骤。 17．（本小题满分 13 分，（1）小问 5 分，（2）小问 8 分） 端午节吃粽子是我国的传统习俗，设一盘中装有 10 个粽子，其中豆沙粽 2 个，肉粽 3 个，白粽 5 个， 这三种粽子的外观完全相同，从中任意选取 3 个。 （1）求三种粽子各取到 1 个的概率； （2）设 X 表示取到的豆沙粽个数，求 X 的分布列与数学期望 18．（本小题满分 13 分，（1）小问 7 分，（2）小问 6 分） 已知函数   2sin sin 3 cos2f x x x x   （1）求  fx的最小正周期和最大值； （2）讨论 在 2,63   上的单调性. 19．（本小题满分 13 分，（1）小问 4 要，（2）小问 9 分） 如题（19）图，三棱锥 P ABC 中，PC  平面 , 3, . ,2ABC PC ACB D E   分别为线段 ,AB BC 上的点，且 2, 2 2.CD DE CE EB    （1）证明： DE 平面 PCD [来源:Zxxk.Com] （2）求二面角 A PD C的余弦值。 20．（本小题满分 12 分，（1）小问 7 分，（2）小问 5 分）[来源:Zxxk.Com] 设函数     23 x x axf x a Re  （1）若 在 0x  处取得极值，确定 a 的值，并求此时曲线  y f x 在点   1, 1f 处的切线方 程； （2）若 在 3,  上为减函数，求 a 的取值范围。 21．（本小题满分 12 分，（1）小问 5 分，（2）小问 7 分） 如题（21）图，椭圆   22 2210xy abab    的左、右焦点分别为 12,,FF 过 2F 的直线交椭圆于 ,PQ两 点，且 1PQ PF （1）若 122 2, 2 2PF PF    ，求椭圆的标准方程 （2）若 1 ,PF PQ 求椭圆的离心率 .e 22．（本小题满分 12 分，（1）小问 4 分，（2）小问 8 分） 在数列 na 中，  2 1 1 13, 0n n n na a a a a n N       （1）若 0, 2,   求数列 na 的通项公式；[来源:学科网] （2）若  00 0 1 , 2 , 1,k N kk     证明： 0 1 00 11223 1 2 1kakk   