高考文科数学复习备课课件：第七节　函数的图象

高考文科数学复习备课课件：第七节　函数的图象

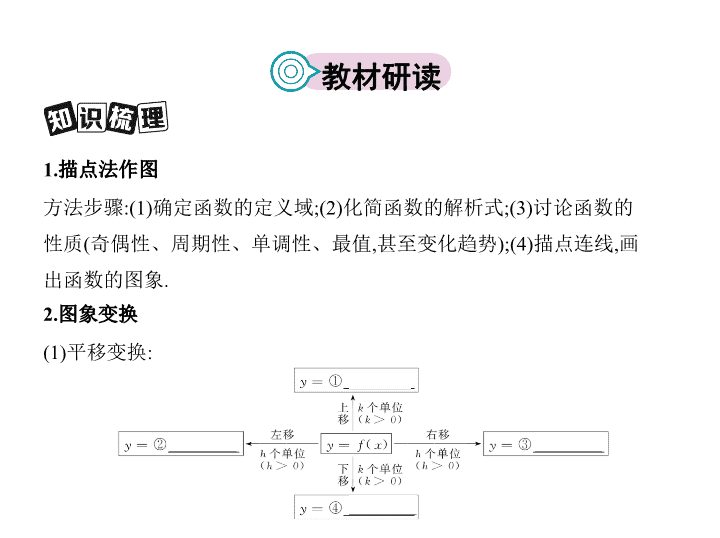
文数 课标 版 第七节　函数的图象 1.描点法作图 方法步骤:(1)确定函数的定义域;(2)化简函数的解析式;(3)讨论函数的 性质(奇偶性、周期性、单调性、最值,甚至变化趋势);(4)描点连线,画 出函数的图象. 2.图象变换 (1)平移变换: 教材研读 (2)伸缩变换: y = f ( x )   y =⑤      f ( ωx )     ; y = f ( x )   y =⑥      Af ( x )     . (3)对称变换: y = f ( x )   y =⑦ 　- f ( x )     ; y = f ( x )   y =⑧      f (- x )     ; y = f ( x )   y =⑨ 　- f (- x )     . (4)翻折变换: y = f ( x )   y =⑩      f (| x |)     ; y = f ( x )   y =   　| f ( x )|     .   (1)当 x ∈(0,+ ∞ )时,函数 y =| f ( x )|与 y = f (| x |)的图象相同.   ( × ) (2)函数 y = af ( x )与 y = f ( ax )( a >0且 a ≠ 1)的图象相同.   ( × ) (3)函数 y = f ( x )与 y =- f ( x )的图象关于原点对称.   ( × ) (4)若函数 y = f ( x )满足 f (1+ x )= f (1- x ),则函数 f ( x )的图象关于直线 x =1对称.   (√) (5)将函数 y = f (- x )的图象向右平移1个单位得到函数 y = f (- x -1)的图象.   ( × )   　　判断下列结论的正误(正确的打“√”,错误的打“ × ”) 1.函数 y = x | x |的图象大致是   (　　)   答案     A     y = x | x |=   为奇函数,奇函数图象关于原点对称. 2.已知图①中的图象是函数 y = f ( x )的图象,则图②中的图象对应的函数 可能是   (　　)   A. y = f (| x |)　    B. y =| f ( x )| C. y = f (-| x |)　    D. y =- f (-| x |) 答案     C　∵题图②中的图象是在题图①的基础上,去掉函数 y = f ( x )的 图象在 y 轴右侧的部分,然后将 y 轴左侧图象翻折到 y 轴右侧得来的,∴题 图②中的图象对应的函数可能是 y = f (-| x |).故选C. 3.(2016广西桂林高考一调)函数 y =( x 3 - x )2 | x | 的图象大致是   (　　)   答案     B　由于函数 y =( x 3 - x )2 | x | 为奇函数,故它的图象关于原点对称,当0 < x <1时, y <0;当 x >1时, y >0,故选B. 4.函数 f ( x )的图象是两条直线的一部分(如图所示),其定义域为[-1,0) ∪ (0,1],则不等式 f ( x )- f (- x )>-1的解集是   (　　)   A.{ x |-1 ≤ x ≤ 1且 x ≠ 0} B.{ x |-1 ≤ x <0} C.   D.   答案     D　由图可知, f ( x )为奇函数, ∴ f (- x )=- f ( x ), ∴ f ( x )- f (- x )>-1 ⇔ 2 f ( x )>-1 ⇔ f ( x )>-   ⇔ -1 ≤ x <-   或0< x ≤ 1.故选D.   5.如图,四个容器高度都相同,将水从容器顶部一个孔中以相同的速度注 入其中,注满为止.用下面对应的图象表示该容器中水面的高度 h 和时间 t 之间的关系,其中不正确的个数为   (　　)     A.1　    B.2　     C.3　    D.4 答案     A　将水从容器顶部一个孔中以相同的速度注入其中,容器中水 面的高度 h 和时间 t 之间的关系可以从高度随时间的变化率上反映出来. 图①应该是匀速的,故下面的图象不正确;②中的变化率应该是越来越 慢的,正确;③中的变化率是先快后慢再快,正确;④中的变化率是先慢后 快再慢,也正确,故只有①是错误的. 考点一　作函数的图象 典例1　 分别画出下列函数的图象: (1) y =|lg x |;　　(2) y =2 x +2 ; 考点突破 (3) y = x 2 -2| x |-1;　　(4) y =   . 解析 　(1) y =   的图象如图①. (2)将 y =2 x 的图象向左平移2个单位即可得到 y =2 x +2 的图象,如图②. (3) y =   的图象如图③. (4) y =   =1+   ,先作出 y =   的图象, 将其图象向右平移1个单位,再向上平移1个单位, 即得 y =   的图象,如图④. 方法技巧 函数图象的常见画法: (1)直接法.当函数(或变形后的函数)是熟悉的基本函数时,或当易发现 函数的图象是解析几何中熟悉的曲线(如圆、椭圆、双曲线、抛物线 的一部分)时,可根据这些熟悉的函数或曲线的特征直接作出. (2)利用图象变换.若函数图象可由某个基本函数的图象经过平移、翻 折、对称得到,则可利用图象变换作出,但要注意变换顺序,对不能直接 找到基本函数的要先变形. (3)描点法.当上面两种方法都失效时,可采用描点法.为了描少量点就能 得到比较准确的图象,常常需要判断函数的单调性、奇偶性. 注意变形的等价性,不要扩大或缩小变量的取值范围. 1-1　 作出下列函数的图象. (1) y =| x -2|·( x +1); (2) y =|log 2 ( x +1)|. 解析 　(1)当 x ≥ 2,即 x -2 ≥ 0时, y =( x -2)( x +1)= x 2 - x -2=   -   ; 当 x <2,即 x -2<0时, y =-( x -2)( x +1)=- x 2 + x +2=-   +   . ∴ y =   函数图象如图所示.   (2)将函数 y =log 2 x 的图象向左平移1个单位,再将 x 轴下方的部分沿 x 轴翻 折上去,即可得到函数 y =|log 2 ( x +1)|的图象,如图.   考点二　函数图象的识辨 命题角度一　以实际问题为背景的图象识辨 典例2 　某天清晨,小明同学生病了,体温上升,吃过药后感觉好多了,中 午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感 觉身上不那么发烫了.下面大致能反映出小明这一天(0~24时)体温的变 化情况的图是   (　　) 答案     C 解析 　清晨体温上升,吃药后到12时体温下降至基本正常,下午又上升, 然后又下降,只有C选项符合. 2-1　 函数 f ( x )=   的大致图象是   (　　)   答案     B　由函数解析式可得 f ( x )为偶函数,当| x | ≤ 1时, f ( x )=   = y ≥ 0,即 x 2 + y 2 =1,∵ y ≥ 0,∴图象取 x 轴及其上方部分,当 x >1时, f ( x )=   ,其图 象在第一象限单调递减,故选B. 2-2 　已知在函数 y =| x |( x ∈[-1,1])的图象上有一点 P ( t ,| t |),该函数的图象与 x 轴、直线 x =-1及 x = t 围成图形(如图阴影部分)的面积为 S ,则 S 与 t 的函数 关系图象可表示为   (　　)     答案     B　由题意知,当-1< t <0时, S 越来越大,但增长的速度越来越慢. 当 t >0时, S 的增长速度会越来越快,故其图象上的切线斜率逐渐增大, 选B. 典例3     (2016课标全国Ⅰ,9,5分)函数 y =2 x 2 -e | x | 在[-2,2]的图象大致为   (　　)   命题角度二　由解析式确定函数的图象 答案     D 解析 　当 x =2时, y =8-e 2 ∈(0,1),排除A,B;易知函数 y =2 x 2 -e | x | 为偶函数,当 x ∈[0,2]时, y =2 x 2 -e x ,求导得 y '=4 x -e x ,当 x =0时, y '<0,当 x =2时, y '>0,所以存在 x 0 ∈(0,2),使得 y '=0,故选D. 典例4     (2015课标Ⅱ,10,5分)如图,长方形 ABCD 的边 AB =2, BC =1, O 是 AB 的中点.点 P 沿着边 BC , CD 与 DA 运动,记∠ BOP = x .将动点 P 到 A , B 两点距 离之和表示为 x 的函数 f ( x ),则 y = f ( x )的图象大致为   (　　)          命题角度三　借助动点探究函数图象 答案     B 解析　 当点 P 与 C 或 D 重合时,易求得 PA + PB =1+   ;当点 P 为 DC 的中点 时,有 OP ⊥ AB ,则 x =   ,易求得 PA + PB =2 PA =2   .显然1+   >2   ,故当 x =   时, f ( x )没有取到最大值,则C、D选项错误.当 x ∈   时, f ( x )=tan x +   ,不是一次函数,排除A,故选B. 典例5     (2014江西,10,5分)在同一直角坐标系中,函数 y = ax 2 - x +   与 y = a 2 x 3 -2 ax 2 + x + a ( a ∈R)的图象   的是   (　　)   命题角度四　同一坐标系下辨析不同函数图象 解析 　当 a =0时,函数为 y 1 =- x 与 y 2 = x ,排除D.当 a ≠ 0时, y 1 = ax 2 - x +   = a   -   +   ,而 y 2 = a 2 x 3 -2 ax 2 + x + a ,求导得 y ' 2 =3 a 2 x 2 -4 ax +1,令 y ' 2 =0,解得 x 1 =   , x 2 =   ,∴ x 1 =   与 x 2 =   是函数 y 2 的两个极值点.当 a >0时,   <   <   ;当 a <0时,   >   >   ,即二次函数 y 1 的对称轴在函数 y 2 的两个极值点之间,所 以选项B不合要求,故选B. 答案     B 方法技巧 函数图象识辨的常用方法 函数图象的识辨可从以下方面入手: (1)由函数的定义域判断图象的左右位置;由函数的值域判断图象的上 下位置; (2)由函数的单调性判断图象的变化趋势; (3)由函数的奇偶性判断图象的对称性; (4)由函数的周期性识辨图象; (5)由函数的特征点排除不合要求的图象. 考点三　函数图象的应用 典例6 　(1)已知函数 f ( x )= x | x |-2 x ,则下列结论正确的是   (　　) A. f ( x )是偶函数,递增区间是(0,+ ∞ ) B. f ( x )是偶函数,递减区间是(- ∞ ,1) C. f ( x )是奇函数,递减区间是(-1,1) D. f ( x )是奇函数,递增区间是(- ∞ ,0) (2)函数 f ( x )是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图所示,那么 不等式   <0的解集为      . 答案 　(1)C　(2)   ∪   解析 　(1)将函数 f ( x )= x | x |-2 x 去掉绝对值得 f ( x )=   画出函数 f ( x )的图象,如图,观察图象可知,函数 f ( x )的图象关于原点对称,故函数 f ( x ) 为奇函数,且在(-1,1)上单调递减. (2)在   上 y =cos x >0, 在   上 y =cos x <0. 由 f ( x )的图象知在   上   <0, 因为 f ( x )为偶函数, y =cos x 也是偶函数, 所以 y =   为偶函数, 所以   <0的解集为   ∪   . 方法技巧 (1)利用函数的图象可解决方程和不等式的求解问题,如判断方程是否 有解,有多少个解. (2)利用图象,可观察函数的单调性、定义域、值域、最值等. 3-1　 已知函数 f ( x )=| x -2|+1, g ( x )= kx .若方程 f ( x )= g ( x )有两个不相等的实 根,则实数 k 的取值范围是   (　　) A.   　    B.   　    C.(1,2)　    D.(2,+ ∞ ) 答案     B     f ( x )=   如图,作出 f ( x )的图象,其中 A (2,1),则 k OA =   .   要使方程 f ( x )= g ( x )有两个不相等的实根,则函数 f ( x )与 g ( x )的图象有两个 交点,由图可知,   < k <1. 3-2　设函数 f ( x )=| x + a |, g ( x )= x -1,对于任意的 x ∈R,不等式 f ( x ) ≥ g ( x )恒成 立,则实数 a 的取值范围是 　　　     . 答案 　[-1,+ ∞ ) 解析 　如图,要使 f ( x ) ≥ g ( x )恒成立,则- a ≤ 1,∴ a ≥ -1.