- 2021-06-30 发布 |
- 37.5 KB |
- 5页
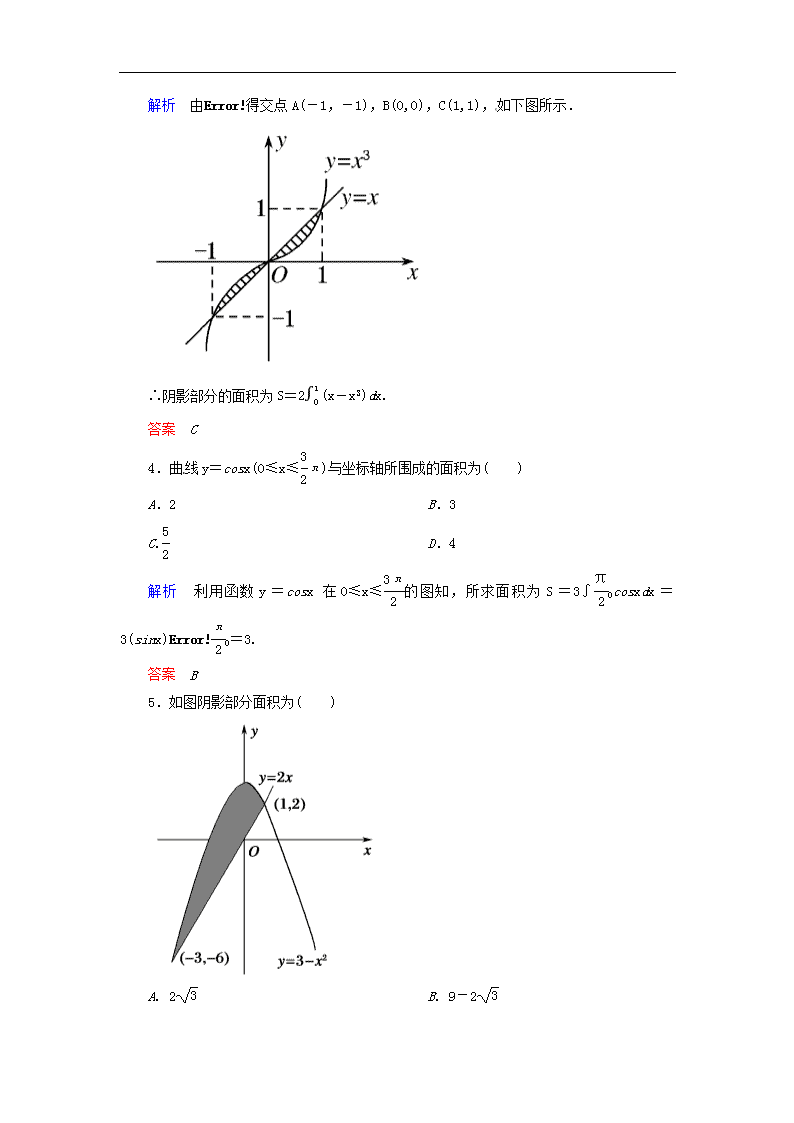
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学 1-7-1 定积分在几何中的应用双基限时训练 新人教版选修2-2
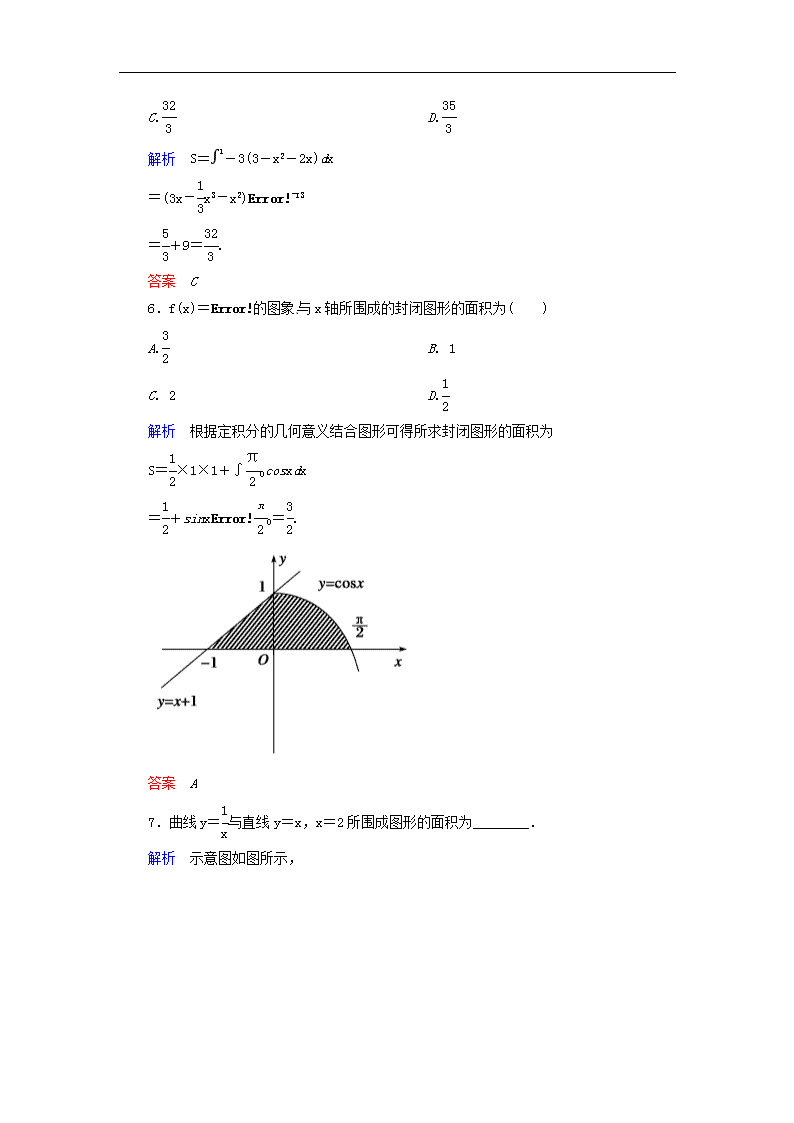
【名师一号】2014-2015学年高中数学 1-7-1 定积分在几何中的应用双基限时训练 新人教版选修2-2 1.由曲线y=f(x)(f(x)≤0),x∈[a,b],x=a,x=b和x轴围成的曲边梯形的面积S等于( ) A.f(x)dx, B.-f(x)dx C.[f(x)-a]dx D.[f(x)-b]dx 答案 B 2.如图,阴影部分的面积为( ) A.f(x)dx B.g(x)dx C.[f(x)-g(x)]dx D.[f(x)+g(x)]dx 解析 阴影部分的面积 S=f(x)dx+|g(x)dx| =f(x)dx-g(x)dx =[f(x)-g(x)]dx. 答案 C 3.曲线y=x3与直线y=x所围成图形的面积等于( ) A.-1(x-x3)dx B.-1(x3-x)dx C.2(x-x3)dx D.2-1(x-x3)dx 解析 由得交点A(-1,-1),B(0,0),C(1,1),如下图所示. ∴阴影部分的面积为S=2(x-x3)dx. 答案 C 4.曲线y=cosx(0≤x≤π)与坐标轴所围成的面积为( ) A.2 B.3 C. D.4 解析 利用函数y=cosx在0≤x≤的图知,所求面积为S=3∫0cosxdx=3(sinx)0=3. 答案 B 5.如图阴影部分面积为( ) A. 2 B. 9-2 C. D. 解析 S=-3(3-x2-2x)dx =(3x-x3-x2) =+9=. 答案 C 6.f(x)=的图象与x轴所围成的封闭图形的面积为( ) A. B. 1 C. 2 D. 解析 根据定积分的几何意义结合图形可得所求封闭图形的面积为 S=×1×1+∫0cosxdx =+sinx0=. 答案 A 7.曲线y=与直线y=x,x=2所围成图形的面积为________. 解析 示意图如图所示, 所求面积为S=(x-)dx=(x2-lnx)=-ln2. 答案 -ln2 8.设函数f(x)=3x2+c,若f(x)dx=5,则实数c的值为________. 解析 ∵f(x)dx=(3x2+c)dx =(x3+cx)=1+c=5, ∴c=4. 答案 4 9.设a>0,若曲线y=与直线x=a,y=0所围成封闭图形的面积为a2,则a=________. 解析 依题意得,由y=与直线x=a,y=0所围成封闭图形的面积S=dx=x=a=a2,∴a=. 答案 10.求正弦曲线y= sinx,x∈[0,]和直线x=及x轴所围成的平面图形的面积. 解 如图,当x∈[0,π]时,曲线 y= sinx位于x轴上方,而当x∈[π,]时,曲线位于x轴下方,因此所求面积应为两部分面积之和. ∴S= sinxdx+|∫π sinxdx| = sinxdx-∫π sinxdx =-cosx+cosxππ =2+1=3. 11.如图,直线y=kx分抛物线y=x-x2与 x轴所围成图形为面积相等的两部分,求k的值. 解 抛物线y=x-x2与x轴两交点的横坐标为x1=0,x2=1,抛物线与x轴所围成的面积S=(x-x2)dx==. 抛物线y=x-x2与直线y=kx两交点的横坐标为0和1-k, ∴S=∫(x-x2-kx)dx==(1-k)3=. ∴(1-k)3=,k=1-=1-. 12.求曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成图形(如图阴影部分)的面积的最小值. 解 由定积分与微积分基本定理得S=S1+S2=(t2-x2)dx+(x2-t2)dx=(t2x-x3)+=t3-t3+-t2-t3+t3=t3-t2+,t∈(0,1). S′=4t2-2t=2t(2t-1). 当0查看更多