2019届二轮复习割补法第1课学案（全国通用）

2019届二轮复习割补法第1课学案（全国通用）

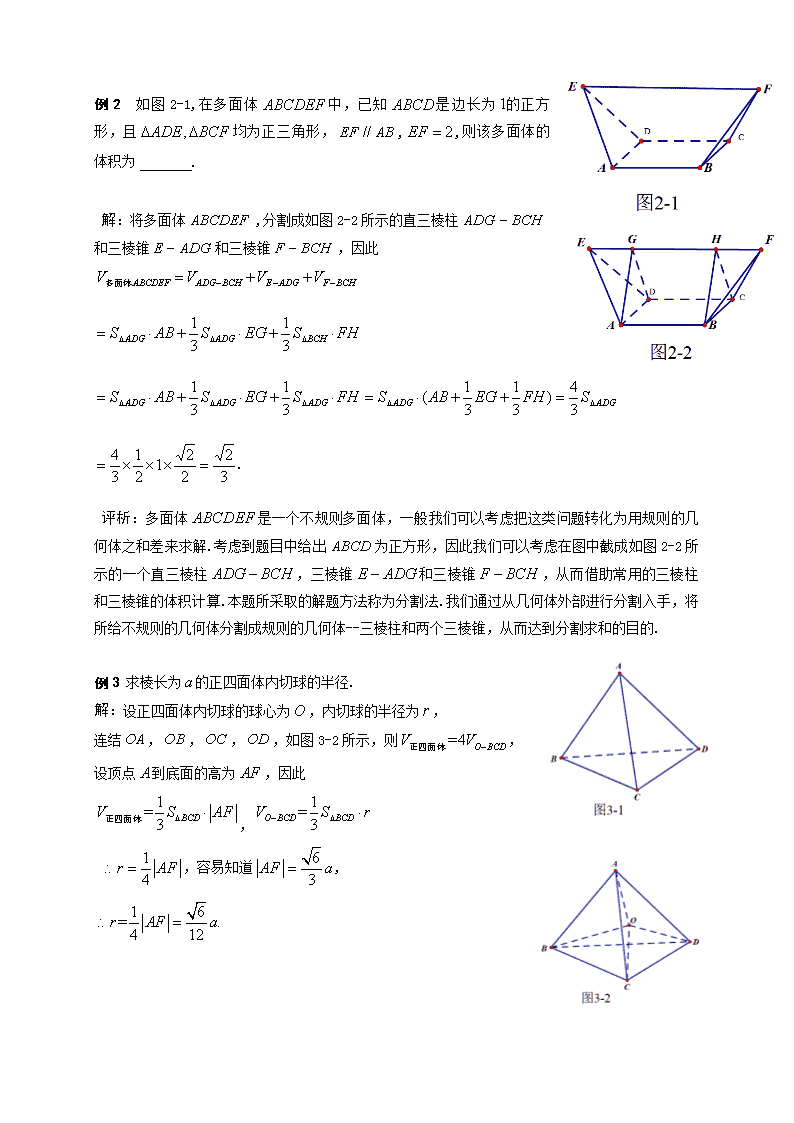
中学数学解题思想方法--割补法（1） ‎ 1 内容概述 普通高中《数学课程标准》中指出：学生能从空间几何体的整体观察入手，认识空间图形，了解一些简单几何体体积的计算方法.割补法就是在求简单几何体的体积中常用的解题方法.‎ 立体几何中的割补法的运用一般是通过将复杂的、不规则的、不易认识的几何体，通过“分割”或者“补形”转化为简单的、规则的、易于认识的几何体，从而解决问题的一种解题方法.‎ ‎ 通过几何体的割补能发现未知几何体与已知几何体的内在联系，提高空间想象能力.割补法的运用蕴含了一种构造的思想方法，反映了对立、统一的辩证思想.本专题将从“补形”、“分割”和 “割补的灵活应用”三个方面进行阐述.本讲着重从前两个方面进行讲解.‎ 2 例题示范 例1 已知如图1-1所示，三棱锥的每相对的两条棱相等，棱长分别为，求三棱锥的体积.‎ ‎ ‎ ‎ ‎ ‎ 解：设补成的长方体的三度分别为，则，补出的四个三棱锥的体积相等，都等于，且，解得 ‎.‎ 评析：一般地如果按常规求法需要求出三棱锥的底面积和对应的高，而本例中高很难求出，因此需要我们重新审视条件寻找其他解决问题的途径.由已知三组相对的棱相等这一特点，联想长方体对面不平行的对角线恰好组成对棱相等的三棱锥，可以把三棱锥补成长方体，如图1-2所示，长方体可以看成由三棱锥和四个相同体积的易于计算的三棱锥组成.本题所采取的解题方法为补形法.难点在于如何利用“对棱相等”这一特点，不拘泥于在所给几何体求体积，联想长方体大胆构造，通过将对棱相等的三棱锥补形成长方体，匠心独具，极大地降低了计算量.类似地，可以将正四面体补形成正方体，将三条棱互相垂直的三棱锥补形成长方体或正方体求三棱锥的体积.‎ ‎ ‎ 例2 如图2-1,在多面体中，已知是边长为的正方形，且均为正三角形，,,则该多面体的体积为.‎ ‎ ‎ ‎ 解：将多面体,分割成如图2-2所示的直三棱柱和三棱锥和三棱锥，因此 ‎.‎ ‎ 评析：多面体是一个不规则多面体，一般我们可以考虑把这类问题转化为用规则的几何体之和差来求解.考虑到题目中给出为正方形，因此我们可以考虑在图中截成如图2-2所示的一个直三棱柱，三棱锥和三棱锥，从而借助常用的三棱柱和三棱锥的体积计算.本题所采取的解题方法称为分割法.我们通过从几何体外部进行分割入手，将所给不规则的几何体分割成规则的几何体--三棱柱和两个三棱锥，从而达到分割求和的目的.‎ 例3 求棱长为的正四面体内切球的半径.‎ 解：设正四面体内切球的球心为，内切球的半径为，‎ 连结，，，，如图3-2所示，则，‎ 设顶点到底面的高为，因此 ‎， ‎ ‎ ，容易知道,‎ ‎ ‎ 评析：要想求出棱长为的正四面体的内切球的半径，必须知道球心的位置，而球心的位置比较难找.我们不妨假设球心为，连结，，，，这样我们就把正四面体分割成四个全等的三棱锥如图3-2所示，而且到正四面体各个面的距离就是内切球的半径.因此.不难看出正四面体和三棱锥共底面，所以我们只要求出正四面体的高，它的即为内切球的半径.本题所采取的解题方法为分割法.分割的点在几何体内部，这也是本题的难点所在.分割后主要利用部分与整体的关系来解决问题.实际并没有分割几何体，只是利用了分割的方法.‎ 1 配套练习 ‎1.如图4-1所示，已知底面半径为的圆柱被一个平面所截，剩下部分的母线长最小值为，最大值为，求这个几何体的体积.‎ ‎ ‎ ‎2.棱长为的正四面体内切球的体积为.‎ ‎3.如图，在四棱锥中，，为矩形, ,‎ 是球表面上的五个点，求球的体积________.‎ 答案： ‎ ‎1.解：补上一个相同的几何体如图4-2所示，可得底面半径为，高为的圆柱，‎ ‎，又 ，因此这个几何体的体积为.‎ ‎2..‎ ‎3..‎