高考数学复习课时提能演练(十四) 2_11

高考数学复习课时提能演练(十四) 2_11

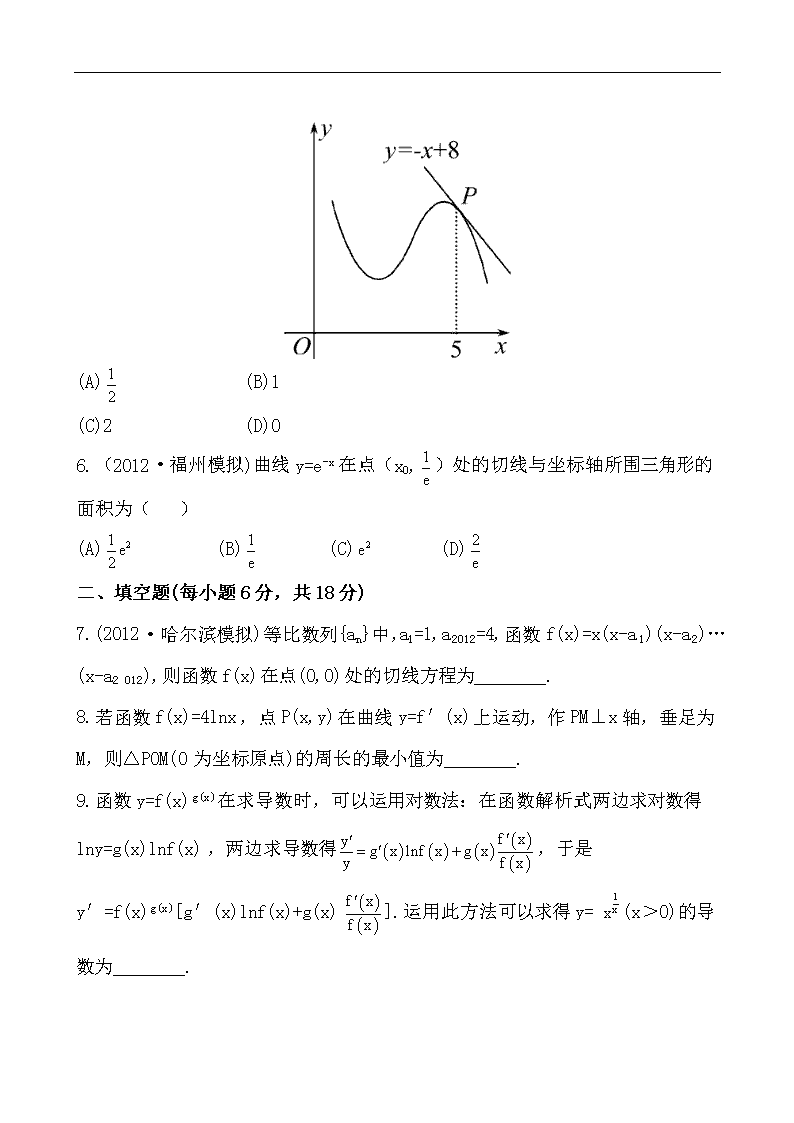
‎ ‎ 课时提能演练(十四)‎ ‎(45分钟 100分)‎ 一、选择题(每小题6分，共36分)‎ ‎1.曲线y= 在点(-1,-1)处的切线方程为( )‎ ‎(A)y=2x+1 (B)y=2x-1‎ ‎(C)y=-2x-3 (D)y=-2x-2‎ ‎2.(2012·宿州模拟)若f(x)=2xf′(1)+x2，则f′(0)等于( )‎ ‎(A)2 (B)0 (C)-2 (D)-4‎ ‎3.y=sinx+tcosx在x=0处的切线方程为y=x+1，则t等于( )‎ ‎(A)1 (B)2 (C)-1 (D)0‎ ‎4.（预测题）已知函数f(x)=xlnx.若直线l过点(0,-1)，并且与曲线y=f(x)相切，则直线l的方程为( )‎ ‎(A)x+y-1=0 (B)x-y-1=0‎ ‎(C)x+y+1=0 (D)x-y+1=0‎ ‎5.（2012·厦门模拟）如图，函数y=f(x)的图象在点P（5，f(5)）处的切线方程是y=-x+8,则f(5)+f′(5)=（ ）‎ ‎(A) (B)1‎ ‎(C)2 (D)0‎ ‎6.（2012·福州模拟)曲线y=e-x在点（x0,）处的切线与坐标轴所围三角形的面积为（ ）‎ ‎(A) (B) (C) (D)‎ 二、填空题(每小题6分，共18分)‎ ‎7.(2012·哈尔滨模拟)等比数列{an}中，a1=1,a2 012=4,函数f(x)=x(x-a1)(x-a2)…(x-a2 012),则函数f(x)在点(0,0)处的切线方程为________.‎ ‎8.若函数f(x)=4lnx，点P(x,y)在曲线y=f′(x)上运动，作PM⊥x轴，垂足为M，则△POM(O为坐标原点)的周长的最小值为________.‎ ‎9.函数y=f(x)g(x)在求导数时，可以运用对数法：在函数解析式两边求对数得lny=g(x)lnf(x)，两边求导数得，于是 y′=f(x)g(x)[g′(x)lnf(x)+g(x)].运用此方法可以求得y= (x＞0)的导数为________.‎ 三、解答题(每小题15分，共30分)‎ ‎10.已知函数f(x)满足如下条件：当x∈(-1,1]时，f(x)=ln(x+1)，且对任意 x∈R，都有f(x+2)=‎2f(x)+1.‎ ‎(1)求函数f(x)的图象在点(0,f(0))处的切线方程；‎ ‎(2)求当x∈(2k-1,2k+1]，k∈N*时，函数f(x)的解析式.‎ ‎11.（易错题）函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且函数y=f(x)和y=g(x)的图象在其与坐标轴的交点处的切线互相平行，求此时平行线的距离.‎ ‎【探究创新】‎ ‎(16分)已知曲线Cn：y=nx2，点Pn(xn,yn)(xn＞0,yn＞0)是曲线Cn上的点(n=1,2，…).‎ ‎(1)试写出曲线Cn在点Pn处的切线ln的方程，并求出ln与y轴的交点Qn的坐标；‎ ‎(2)若原点O(0,0)到ln的距离与线段PnQn的长度之比取得最大值，试求点Pn的坐标(xn,yn).‎ 答案解析 ‎1.【解析】选A.因为y′=，所以，在点(-1,-1)处的切线斜率 k=y′|x=-1==2，所以，切线方程为y+1=2(x+1)，即y=2x+1，故选A.‎ ‎2.【解题指南】对f(x)求导时要注意到f′(1)为常数，先求出f′(1)，再求 f′(0).‎ ‎【解析】选D.f′(x)=‎2f′(1)+2x，∴令x=1，得 f′(1)=-2，∴f′(0)=‎2f′(1)=-4.‎ ‎3.【解析】选A.∵y′=cosx-tsinx，当x=0时，y=t，y′=1，‎ ‎∴切线方程为y=x+t，比较可得t=1.‎ ‎4.【解析】选B.f′(x)=lnx+1，x＞0，设切点坐标为(x0,y0)，则y0=x0lnx0，‎ 切线的斜率为lnx0+1，所以lnx0+1=，解得x0=1，y0=0，‎ 所以直线l的方程为x-y-1=0.‎ ‎5.【解析】选C.由题意可知f(5)=-5+8=3,f′(5)=-1,‎ ‎∴f(5)+f′(5)=3-1=2.‎ ‎6. 【解析】选D.由y=e-x得y′=-e-x,‎ 又∴x0=1,‎ ‎=,切线方程为 令x=0,得y=,‎ 令y=0,得x=2,‎ ‎7.【解析】f′(x)=(x-a1)(x-a2)…(x-a2 012)+x·(x-a2)(x-a3)…‎ ‎(x-a2 012)+x(x-a1)(x-a3)…(x-a2 012)+…+x(x-a1)(x-a2)…(x-a2 011),‎ ‎∴f′(0)=(-a1)·(-a2)…(-a2 012)=(a‎1a2 012)1 006=22 012,‎ ‎∴切线方程为y=22 012x.‎ 答案：y=22 012x ‎【变式备选】已知函数f(x)=,g(x)=alnx,a∈R.若曲线y=f(x)与曲线y=g(x)相交，且在交点处有相同的切线，求a的值及该切线的方程.‎ ‎【解析】f′(x)= ,g′(x)= (x＞0),‎ 由已知得：解得a=e,x=e2.‎ ‎∴两条曲线交点的坐标为(e2,e)，‎ 切线的斜率为k=f′(e2)=,‎ 所以切线的方程为y-e=(x-e2),‎ 即x-2ey+e2=0.‎ ‎8.【解析】f′(x)= (x>0)，∴P(x, )，M(x,0)，‎ ‎∴△POM的周长为x++ ‎ ‎(当且仅当x=2时取得等号).‎ 答案：‎ ‎9.【解析】对y=(x＞0)两边取对数得 lny=lnx，两边求导得，‎ ‎∴.‎ 答案：y′= ‎ ‎10.【解析】(1)x∈(-1,1]时，f(x)=ln(x+1)，f′(x)= ，‎ 所以，函数f(x)的图象在点(0,f(0))处的切线方程为y-f(0)=f′(0)(x-0)，即y=x. ‎ ‎(2)因为f(x+2)=‎2f(x)+1，‎ 所以，当x∈(2k-1,2k+1]，k∈N*时，x-2k∈(-1,1]，‎ f(x)=‎2f(x-2)+1=‎22f(x-4)+2+1‎ ‎=‎23f(x-6)+22+2+1=…‎ ‎=2kf(x-2k)+2k-1+2k-2+…+2+1‎ ‎=2kln(x-2k+1)+2k-1.‎ ‎11.【解析】f′(x)=aex，g′(x)= ，y=f(x)的图象与坐标轴的交点为(0,a)，y=g(x)的图象与坐标轴的交点为(a,0)，由题意得f′(0)=g′(a)，即a=.‎ 又∵a＞0，∴a=1.‎ ‎∴f(x)=ex，g(x)=lnx，∴函数y=f(x)和y=g(x)的图象在其与坐标轴的交点处的切线方程分别为：x-y+1=0,x-y-1=0，∴两平行切线间的距离为.‎ ‎【方法技巧】求曲线的切线方程 求曲线的切线方程，一般有两种情况：‎ ‎(1)求曲线y=f(x)在(x0,f(x0))处的切线，此时曲线斜率为f′(x0)，利用点斜式可得切线方程为y-f(x0)=f′(x0)(x-x0)；‎ ‎(2)求曲线y=f(x)过点P(x0,y0)的切线，此时需要设出切点A(xA,yA),表示出切线方程，再把P(x0,y0)的坐标代入切线方程，解得xA，进而写出切线方程.‎ ‎【变式备选】已知函数f(x)=(x-a)2(x-b)(a,b∈R,a＜b).‎ ‎(1)当a=1，b=2时，求曲线y=f(x)在点(2，f(2))处的切线方程.‎ ‎(2)设x1,x2是f′(x)=0的两个根，x3是f(x)的一个零点，且x3≠x1，x3≠x2.‎ 证明：存在实数x4，使得x1,x2,x3,x4按某种顺序排列后成等差数列，并求x4.‎ ‎【解析】(1)当a=1,b=2时，f(x)=(x-1)2(x-2),‎ 因为f′(x)=(x-1)(3x-5)，故f′(2)=1，f(2)=0,‎ 所以f(x)在点(2,0)处的切线方程为y=x-2.‎ ‎(2)因为f′(x)=3(x-a)(x-)，‎ 由于a

查看更多