2021版高考数学一轮复习核心素养测评四十一直线与平面平面与平面垂直苏教版

2021版高考数学一轮复习核心素养测评四十一直线与平面平面与平面垂直苏教版

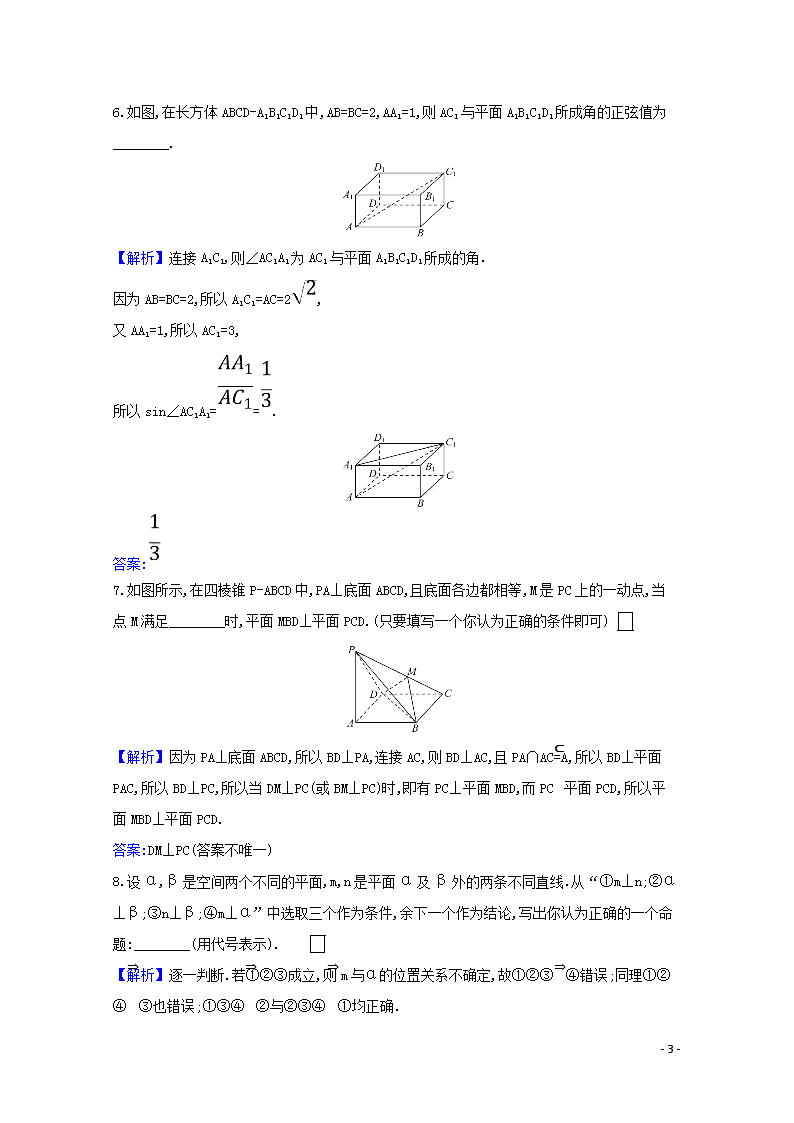
核心素养测评四十一 直线与平面、平面与平面垂直 ‎(30分钟　60分)‎ 一、选择题(每小题5分,共25分)‎ ‎1.α,β,γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件 是 (　　)‎ A.n⊥α,n⊥β,m⊥α　 ‎ B.α∩γ=m,α⊥γ,β⊥γ C.α⊥γ,β⊥γ,m⊥α　 ‎ D.α⊥β,α∩β=l,m⊥l ‎【解析】选A.由n⊥α,n⊥β知α∥β,又m⊥α,所以m⊥β.所以A正确.‎ ‎2.如图所示,b,c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,‎ D∈b,则△ACD是 (　　)‎ A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形 ‎【解析】选B.因为a⊥b,b⊥c,a∩c=B,所以b⊥平面ABC,所以AD⊥AC,故△ACD为直角三角形.‎ ‎3.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下面结论正确的是 (　　)‎ A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC - 8 -‎ ‎【解析】选D.在平面图形中CD⊥BD,折起后仍有CD⊥BD,由于平面ABD⊥平面BCD,故CD⊥平面ABD,所以CD⊥AB,又AB⊥AD,AD∩CD=D,故AB⊥平面ADC,又因为AB⊂平面ABC,所以平面ABC⊥平面ADC.‎ ‎4.如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上一点(不同于A、B)且PA=AC,则二面角P-BC-A的大小为 (　　)‎ A.60° B.30° C.45° D.15°‎ ‎【解析】选C.由条件得PA⊥BC,AC⊥BC,又PA∩AC=A,所以BC⊥平面PAC,所以∠PCA为二面角P-BC-A的平面角.在Rt△PAC中,由PA=AC得∠PCA=45°.‎ ‎5.如图,正三角形PAD所在平面与正方形ABCD所在平面互相垂直,O为正方形ABCD的中心,M为正方形ABCD内一点,且满足MP=MC,则点M的轨迹为 (　　)‎ ‎【解析】选A.取AD的中点E,连接PE,PC,CE.‎ 由PE⊥AD知PE⊥平面ABCD,‎ 从而平面PEC⊥平面ABCD,取PC,AB的中点F,G,连接DF,DG,FG,‎ 由PD=DC知DF⊥PC,由DG⊥EC知,DG⊥平面PEC,又PC⊂平面PEC,‎ 所以DG⊥PC,DF∩DG=D,所以PC⊥平面DFG,又点F是PC的中点,‎ 因此,线段DG上的点满足MP=MC.‎ 二、填空题(每小题5分,共15分)‎ - 8 -‎ ‎6.如图,在长方体ABCD-A1B‎1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B‎1C1D1所成角的正弦值为________. ‎ ‎【解析】连接A‎1C1,则∠AC‎1A1为AC1与平面A1B‎1C1D1所成的角.‎ 因为AB=BC=2,所以A‎1C1=AC=2,‎ 又AA1=1,所以AC1=3,‎ 所以sin∠AC‎1A1==.‎ 答案:‎ ‎7.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可)  ‎ ‎【解析】因为PA⊥底面ABCD,所以BD⊥PA,连接AC,则BD⊥AC,且PA∩AC=A,所以BD⊥平面PAC,所以BD⊥PC,所以当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD,而PC⊂平面PCD,所以平面MBD⊥平面PCD.‎ 答案:DM⊥PC(答案不唯一)‎ ‎8.设α,β是空间两个不同的平面,m,n是平面α及β外的两条不同直线.从“①m⊥n;②α⊥β;③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题:________(用代号表示).  ‎ ‎【解析】逐一判断.若①②③成立,则m与α的位置关系不确定,故①②③⇒④错误;同理①②④⇒③也错误;①③④⇒②与②③④⇒①均正确.‎ - 8 -‎ 答案:①③④⇒②(或②③④⇒①)‎ 三、解答题(每小题10分,共20分)‎ ‎9.如图,在三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD. ‎ ‎(1)求证:CD⊥平面ABD. ‎ ‎(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.‎ ‎【解析】(1)因为AB⊥平面BCD,CD⊂平面BCD,‎ 所以AB⊥CD.‎ 又因为CD⊥BD,AB∩BD=B,‎ 所以CD⊥平面ABD.‎ ‎(2)由AB⊥平面BCD,得AB⊥BD.‎ 又AB=BD=1,所以S△ABD=×12=.‎ 因为M是AD的中点,‎ 所以S△ABM=S△ABD=.‎ 根据(1)知,CD⊥平面ABD,‎ 则三棱锥C