丰台区2016届高三一模数学（文）试题及答案

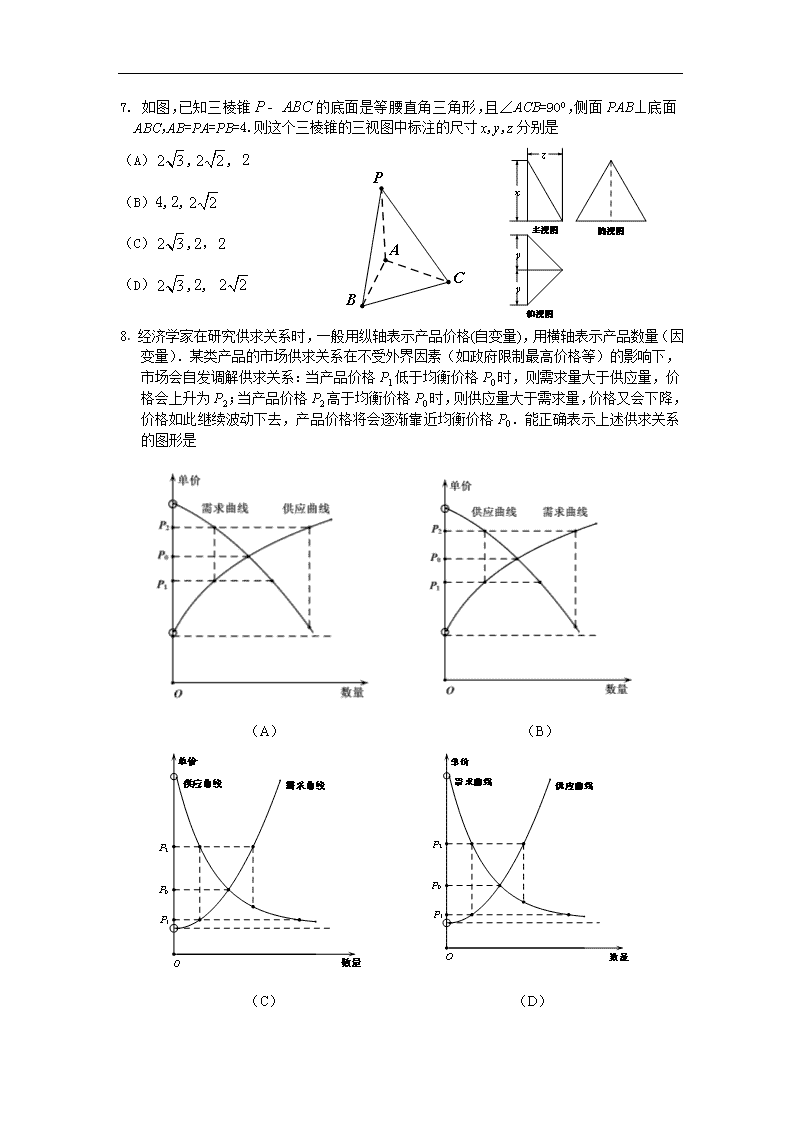
丰台区2016届高三一模数学（文）试题及答案

‎ 丰台区2015—2016学年度第二学期统一练习（一） 2016.3‎ 高三数学（文科）‎ 第一部分 （选择题 共40分） ‎ 一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．‎ ‎1. 已知全集 ，集合 ，集合 ，则集合=‎ ‎（A） （B） ‎ ‎（C） （D）‎ ‎2. 下列函数在其定义域上既是奇函数又是增函数的是 ‎（A） （B） ‎ ‎（C） （D）‎ ‎3. 某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们每场比赛得分的情况用茎叶图表示，如图，则甲、乙两名运动员得分的中位数分别为 ‎（A） 20、18 （B）13、19 ‎ ‎（C）19、13 （D）18、20‎ ‎4. 已知直线和平面，，∥,那么“”是“∥”的 ‎（A）充分而不必要条件 （B）必要而不充分条件 ‎（C）充分必要条件 （D）既不充分也不必要条件 ‎5.已知双曲线的一个焦点F，点P在双曲线的一条渐近线上，点O为双曲线的对称中心，‎ 若△OFP为等腰直角三角形，则双曲线的离心率为 ‎（A） （B） （C）2 （D）‎ ‎6. 已知等比数列{}中，且，那么的值是 ‎（A）15 （B）31 （C）63 （D）64‎ ‎7. 如图，已知三棱锥的底面是等腰直角三角形，且∠ACB=90O，侧面PAB⊥底面ABC，AB=PA=PB=4.则这个三棱锥的三视图中标注的尺寸x,y,z分别是 ‎（A）,, 2‎ ‎（B）4,2, ‎ ‎（C）,2，2‎ ‎（D）,2, ‎ ‎8. 经济学家在研究供求关系时，一般用纵轴表示产品价格(自变量)，用横轴表示产品数量（因变量）．某类产品的市场供求关系在不受外界因素（如政府限制最高价格等）的影响下，市场会自发调解供求关系：当产品价格P1低于均衡价格P0时，则需求量大于供应量，价格会上升为P2；当产品价格P2高于均衡价格P0时，则供应量大于需求量，价格又会下降，价格如此继续波动下去，产品价格将会逐渐靠近均衡价格P0．能正确表示上述供求关系的图形是 ‎（A） （B）‎ ‎ ‎ ‎（C） （D）‎ ‎ ‎ 第二部分 （非选择题 共110分）‎ 二、填空题共6小题，每小题5分，共30分．‎ ‎9.在锐角△ABC中，角A，B，C所对应的边分别为a,b,c，若，则 ∠A=_________．‎ ‎10.已知△ABC中，AB=4，AC=3，∠CAB=90o，则___________．‎ ‎11.已知圆，则圆被动直线所截得的弦长__________．‎ ‎12.已知，则函数的最小值为________． ‎ ‎13. 已知满足目标函数的最大值为5，则的值为 ．‎ ‎14.函数． ‎ ‎ ① 当b=0时，函数f(x)的零点个数_______；‎ ‎ ② 若函数f(x)有两个不同的零点，则b的取值范围________．‎ 三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．‎ ‎15.（本小题共13分）‎ 已知函数．‎ ‎(Ⅰ)求函数的最小正周期；‎ ‎(Ⅱ)求在区间上的最大值和最小值.‎ ‎16. （本小题共13分）‎ 下图是根据某行业网站统计的某一年1月到12月（共12个月）的山地自行车销售量（1k代表1000辆）折线图，其中横轴代表月份，纵轴代表销售量，由折线图提供的数据回答下列问题：‎ ‎（Ⅰ）在一年中随机取一个月的销售量，估计销售量不足200k的概率；‎ ‎（Ⅱ）在一年中随机取连续两个月的销售量，估计这连续两个月销售量递增（如2月到3月递增）的概率；‎ ‎（Ⅲ）根据折线图，估计年平均销售量在哪两条相邻水平平行线线之间（只写出结果，不要过程）.‎ ‎17. （本小题共14分）‎ 已知在△ABC中，∠B=90o，D，E分别为边BC，AC的中点，将△CDE沿DE翻折后，使之成为四棱锥（如图）.‎ ‎（Ⅰ）求证：DE⊥平面；‎ ‎（Ⅱ）设平面平面，求证：AB∥l；‎ ‎（Ⅲ）若，，，F为棱上一点，设，当为何值时，三棱锥的体积是1？‎ ‎18. （本小题共13分）‎ 已知函数，数列满足：.‎ ‎ （Ⅰ）求数列的通项公式；‎ ‎ （Ⅱ）设数列的前项和为，求数列的前项和.‎ ‎19 . （本小题共14分）‎ 已知函数．‎ ‎（Ⅰ）求曲线在处的切线的方程；‎ ‎（Ⅱ）若函数在定义域内是单调函数，求的取值范围；‎ ‎（Ⅲ）当时，（Ⅰ）中的直线l与曲线有且只有一个公共点，求的取值范围.‎ ‎20. （本小题共13分）‎ 已知椭圆:过点A（2，0），离心率，斜率为 直线过点M（0，2），与椭圆C交于G，H两点（G在M，H之间），与轴交于点B. ‎ ‎ （Ⅰ）求椭圆C的标准方程；‎ ‎ （Ⅱ）P为轴上不同于点B的一点，Q为线段GH的中点，设△HPG的面积为， 面积为，求的取值范围. ‎ 丰台区2016年高三年级第二学期数学统一练习（一）‎ 数 学（文科）参考答案 一、选择题：本大题共8小题，每小题5分，共40分。‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 B A C A B B C D 二、填空题：本大题共6小题，每小题5分，共30分．‎ ‎9. 10.16 11. 12. 3 13. 14 . 0 ；‎ ‎ ‎ 注：14题第一空2分，第二空3分。‎ 三、解答题：本大题共6小题，共80分。解答应写出文字说明，演算步骤或证明过程。‎ ‎15．（本小题共13分）‎ 解： ……………4分 ‎ ……………6分 ‎（Ⅰ）； ……………7分 ‎（Ⅱ）因为，所以， ……………9分 即, ……………11分 由此得到：，此时； ……………12分 ‎，此时． ……………13分 ‎16．（本小题共13分）‎ 解：（Ⅰ）设销售量不足200k为事件A，‎ 这一年共有12个月，‎ 其中1月，2月，6月，11月共4个的销售量不足200k，……………2分 所以． ……………4分 ‎（Ⅱ）设连续两个月销售量递增为事件B，‎ 在这一年中随机取连续两个月的销售量，有1，2月；2，3月；3，4月；4，5月；5，6月；6，7月；7，8月；8，9月；9，10月；10，11月；‎ ‎11，12月共11种取法， ……………6分 其中2，3月，3，4月；4，5月； 6，7月；7，8月；8，9月；‎ ‎11，12月共7种情况的销售量递增， ……………8分 所以． ……………10分 ‎（Ⅲ）在200k~250k这两条水平线之间． ……………13分 ‎17．（本小题共14分）‎ 证明：（Ⅰ）∵∠B=90o，D，E分别为BC，AC的中点 ‎∴DE∥AB ……………1分 ‎∴， ……………3分 又∵ ……………4分 ‎∴DE⊥平面 ……………5分 ‎（Ⅱ）∵DE∥AB，面， 面，‎ ‎∴AB∥面， ……………7分 又∵AB面，面面 ……………9分 ‎∴ AB∥ ……………10分 ‎（Ⅲ）∵，，，‎ ‎∴⊥平面BDE．‎ ‎∵∴ ……………11分 又因为BD=3，AB=2，，‎ ‎∴‎ ‎ ……………13分 解得． ……………14分 ‎18.（本小题共13分）‎ 解： （Ⅰ）∵，‎ ‎∴ ……………2分 即，所以数列是以首项为2，公差为2的等差数列， ………4分 ‎∴ ……………6分 ‎（Ⅱ）∵数列是等差数列，‎ ‎∴ ……………8分 ‎∴ ……………10分 ‎∴‎ ‎ ……………11分 ‎ ……………13分 ‎19.（本小题共14分）‎ 解：（Ⅰ）， ……………1分 因为，所以切点为（1，）． ‎ 又， ……………2分 所以切线，‎ 即. ……………3分 ‎（Ⅱ）①当时，，‎ 所以在上单调递减，符合题意． ……………5分 ‎②当时，设，该抛物线开口向上，且，过点，所以该抛物线与轴相交，交点位于原点两侧，不单调，不符合题意，舍去． ……………6分 综上． ……………7分 ‎（Ⅲ）因为直线l与有且只有一个公共点，‎ 所以方程，‎ 即有且只有一个根． ……………8分 设， ‎ 则，……………10分 ‎①当时，‎ 因为，所以，令，解得；‎ 令，解得；‎ 所以在上单调递增，在上单调递减，‎ 所以，所以符合条件． ……………11分 ‎②当时，则 令，解得；‎ 令，解得或；‎ 所以在上单调递增，在，上单调递减，………12分 ‎ ‎ 因为，所以，．又，所以，即，所以．‎ 所以在上有一个零点，且，所以有两个零点，不符合题意．‎ 综上． ……………14分 ‎20．（本小题共13分）‎ 解：（Ⅰ）由已知得， …………1分 又，所以， …………2分 即， ……………3分 所以椭圆的标准方程为．………4分 ‎（Ⅱ）‎ 设，直线 ． …5分 由得： ……6分 ‎ 所以 ， ‎ 即 ……………7分 ‎∵ ，即．‎ 因为，所以． ……………8分 又，‎ 而， ……9分 ‎， ……………10分 ‎， ……11分 ‎ 设 ‎． ……………13分