2018-2019学年黑龙江省大庆实验中学高二下学期开学考试数学（理）试题 Word版

2018-2019学年黑龙江省大庆实验中学高二下学期开学考试数学（理）试题 Word版

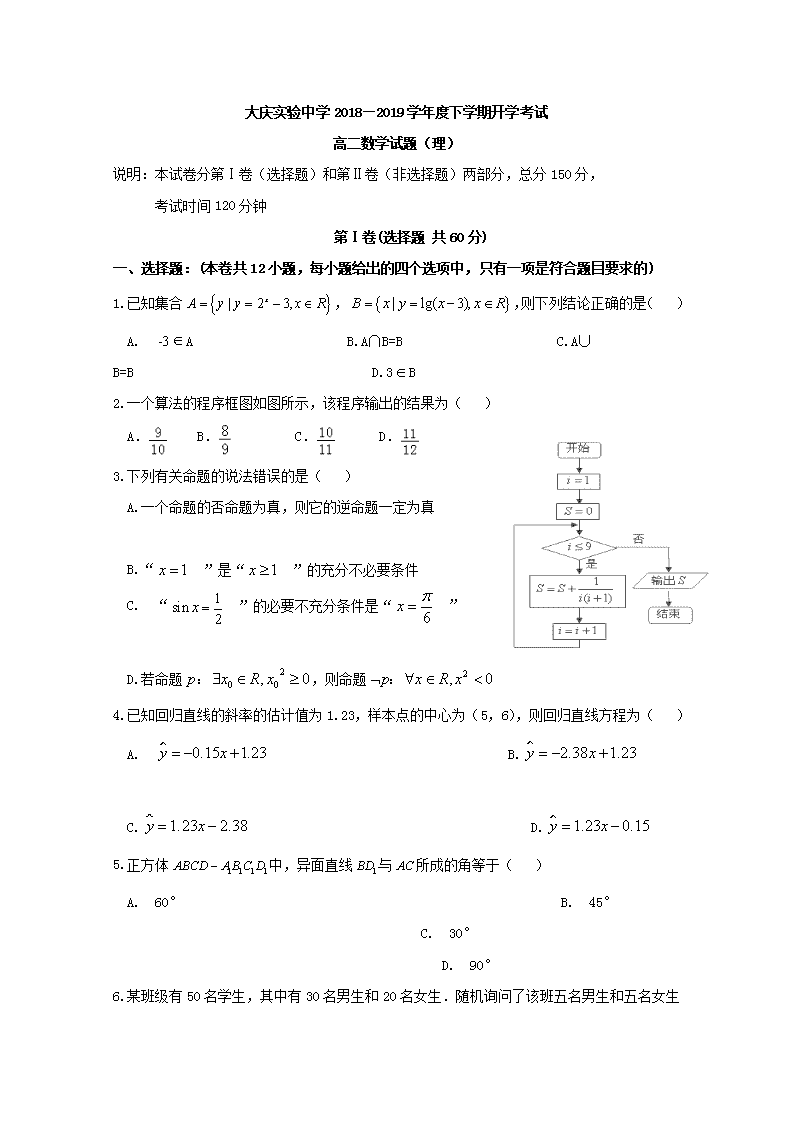
大庆实验中学2018—2019学年度下学期开学考试 高二数学试题（理）‎ 说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，总分150分，‎ 考试时间120分钟 第Ⅰ卷(选择题 共60分)‎ 一、选择题：(本卷共12小题，每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1.已知集合，，则下列结论正确的是（　 ） ‎ A. A        B.A∩B=B         C.A∪B=B               D.3B    ‎ ‎2.一个算法的程序框图如图所示，该程序输出的结果为（　 ）‎ A． B． C． D．‎ ‎3.下列有关命题的说法错误的是（ ） ‎ A.一个命题的否命题为真，则它的逆命题一定为真          ‎ B.“ ”是“ ”的充分不必要条件 C. “ ”的必要不充分条件是“ ”         ‎ D.若命题，则命题 ‎4.已知回归直线的斜率的估计值为1.23，样本点的中心为（5，6），则回归直线方程为（ ） A.            B.            ‎ C.                D.‎ ‎5.正方体中，异面直线与所成的角等于（ ） ‎ A. 60°                           B. 45°                      C. 30°                      D. 90°‎ ‎6.‎ 某班级有50名学生，其中有30名男生和20名女生．随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86,94,88,92,90，五名女生的成绩分别88,93,93,88,93.下列说法一定正确的是（ ） ‎ A. 这种抽样方法是一种分层抽样                 ‎ ‎ B. 这种抽样方法是一种系统抽样 C. 这五名男生成绩的方差小于这五名女生成绩的方差          ‎ D. 该班男生成绩的中位数小于该班女生成绩的中位数 ‎7.圆的半径为4，圆心在轴的正半轴上，直线与圆相切，则圆的方程为（ ）‎ A． B． C． D．‎ ‎8.已知一个进制数与十进制数30相等，那么等于（  ） ‎ A. 4                              B.4或7                    C.5                             D.7‎ ‎9.已知是同一球面上的四个点，其中是正三角形，，则该球的体积为（  ）‎ A.                       B.                         C.                      D.‎ ‎10.定义域和值域均为的函数,定义 ‎，则的根为的n阶不动点，设，则的6阶不动点的个数为( ) ‎ A.6 B.12 C.64 D.36‎ ‎11.F是双曲线的右焦点，过点F向C的一条渐近线引垂线，垂足为点A，交另一条渐近线于点B，若，则的离心率是（ ）‎ A.  B.      C.        D. ‎ ‎12.已知函数，，(为实数，为自然对数的底数)，设，若对 任意的，，，恒成立，则实数的最小值为（ ）‎ A.          B.       C.         D. ‎ 第Ⅱ卷(非选择题 共90分)‎ 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13.=___ _______‎ ‎14.用数学归纳法证明“”时，由 到 时，不 等式左边应添加的项是__________ ‎ ‎15.实数，.设函数的两个极值点为,现向点所在平面区域投掷一个飞镖,则飞镖恰好落入使且的区域的概率为_________‎ ‎16.已知圆的圆心在抛物线上运动，且圆C过点，若为圆在轴上截得的弦，则的取值范围为_________‎ 三、解答题：(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17.（满分10分）已知数列的前n项和，且满足，数列满足，且为等差数列.‎ ‎（1）求数列的通项公式；（2）求数列的前n项和.‎ ‎18.（满分12分）已知向量，设函数.‎ ‎（1）求函数的最小正周期及单调增区间；‎ ‎（2）若的最小值.‎ ‎19. （满分12分） 雾霾天气对城市环境造成很大影响，按照国家环保部发布的标准：居民区的PM2.5（大气中直径小于或等于2.5微米的颗粒物）年平均浓度不得超过35微克/立方米．某市环保部门加强了对空气质量的监测，抽取某居民区监测点的20天PM2.5的日平均浓度的监测数据，制成频率分布表，如（1）问图：‎ ‎（1）根据如下频率分布表，并在所给的坐标系中画出（0，100）的频率分布直方图； ‎ ‎ 组别 ‎ PM2.5浓 度（微克/立方米）‎ ‎ 频数 ‎（天）‎ ‎ 频率 ‎ 第一组 ‎ （0，25]‎ ‎5 ‎ ‎0.25 ‎ ‎ 第二组 ‎ （25，50]‎ ‎10 ‎ ‎0.5 ‎ ‎ 第三组 ‎ （50，75]‎ ‎3‎ ‎0.15 ‎ ‎ 第四组 ‎ （75，100）‎ ‎2 ‎ ‎ 0.1‎ ‎（2）根据频率分布直方图估计该居民区测试点PM2.5日平均浓度的中位数；‎ ‎（3）从样本中PM2.5的日平均浓度超过50微克/立方米的天数中，随机抽取2天，求恰好有一天PM2.5的日平均浓度超过75微克/立方米的概率．‎ ‎20. （满分12分）如图，在四棱锥中，底面为矩形，，，为中点．‎ ‎（1）求证：；‎ ‎（2）求平面PAC和平面PCD所成二面角的大小．‎ ‎21.（满分12分）已知椭圆的离心率为，且椭圆上的点到一个焦点的距离的最小值为．‎ ‎（1）求椭圆的方程；‎ ‎（2）设椭圆的左右顶点分别是、，过点的动直线与椭圆交于，‎ 两点，连接、相交于点，试求点的横坐标的值．‎ ‎22.（满分12分）已知函数．‎ ‎（1）讨论函数的单调区间；‎ ‎（2）若，且恒成立，求的最大值（其中e为自然对数的底数）．‎