2018-2019学年江西省宜丰中学高二上学期期末考试数学（文）试题 Word版

2018-2019学年江西省宜丰中学高二上学期期末考试数学（文）试题 Word版

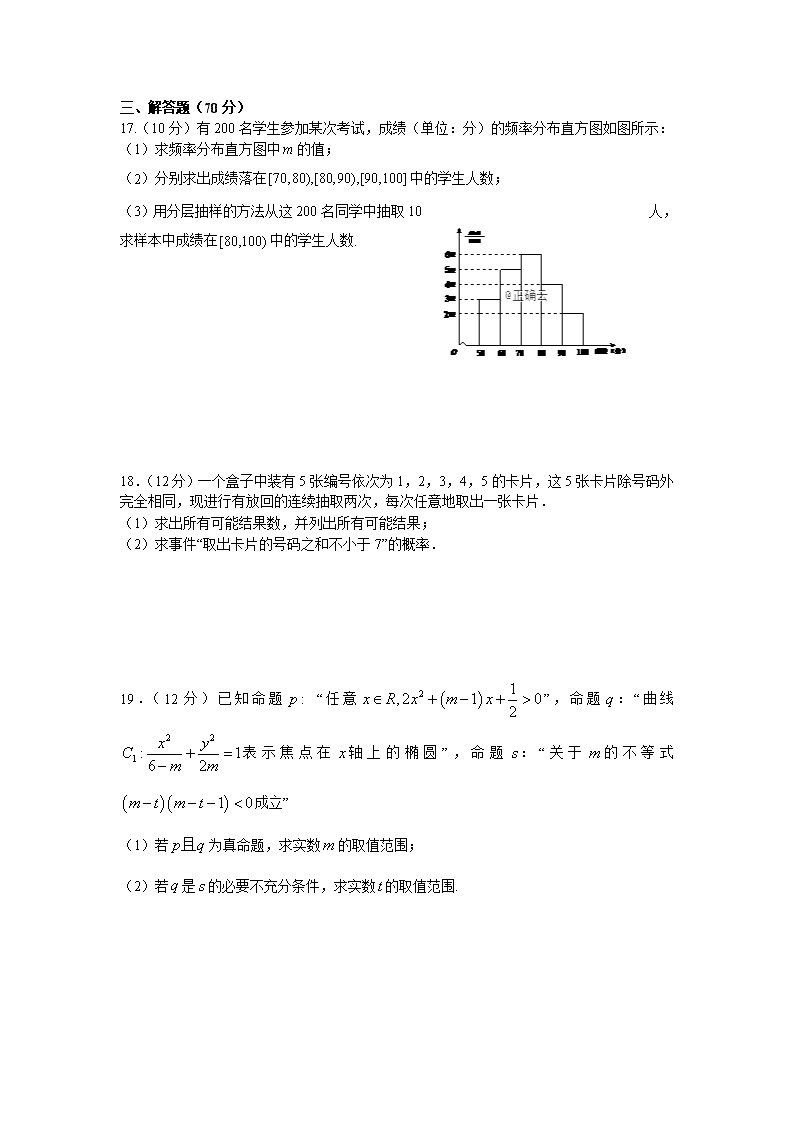
江西省宜丰中学2018-2019学年高二期末考试数学试卷（文科）‎ 组题人:江会芳 审题人:肖双平 一、选择题（每小题5分，共60分）‎ ‎1.命题“”的否定是(　　)‎ A． B．‎ C． D．‎ ‎2.为了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为　(　　)‎ A.50 B.40 C.25 D.20‎ ‎3.以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位：分)．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为(　　)‎ A．2,5 B．5,5 C．5,8 D．8,8‎ ‎4.已知椭圆(m>0)的左焦点为F1(－4，0)，则m＝(　　)‎ A．2 B．3 C．4 D．9‎ ‎5、执行如图所示的程序框图，输出的S值为（　　）‎ A、2 B、 C、 D、‎ ‎6．已知随机变量的值如下表所示，如果与线性相关，且回归直线方程为，则实数的值为( )‎ A. B. C. D. ‎ ‎7.曲线在点（1，2）处的切线方程为（ ）‎ A． B． C． D．‎ ‎8．如果数据的平均数为，方差为，则的平均数和方差分别为（ ）‎ A. B. C. D. ‎ ‎9.小波通过做游戏的方式来确定周末活动，他随机地往单位圆内投掷一点，若此点到圆心的距离大于 ，则周末去看电影；若此点到圆心的距离小于 ，则去打篮球；否则，在家看书．则小波周末不在家看书的概率为 (　 　)‎ A.　　 B．　　　　 C.　　　 D．‎ ‎10．已知抛物线：的焦点为，是上一点，且，则（ ）‎ A. B. C. D. ‎ ‎11．若函数在区间内存在单调递增区间，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎12．已知是定义在上的偶函数，且，当时，，则不等式的解集是( )‎ A. B. C. D. 以上都不正确 二、填空题（每小题5分，共20分）‎ 13． 口袋中有若干红球、黄球与蓝球，从中摸出一个球，摸出红球的概率为0.5，摸出红球或黄球的概率为0.65，则摸出红球或蓝球的概率为___．‎ ‎14.已知函数的极大值点，则=_______.‎ ‎15．有下列四种说法：①，均成立；②若是假命题，则，都是假命题；③命题“若，则”的逆否命题是真命题；④“”是“直线与直线互相垂直”的充分条件．其中正确的命题有__________．‎ 16． 过双曲线的左焦点，作倾斜角为的直线交该双曲线右支于点，若，且，则双曲线的离心率为_____‎ 三、解答题（70分）‎ ‎17.（10分）有200名学生参加某次考试，成绩（单位：分）的频率分布直方图如图所示：‎ ‎（1）求频率分布直方图中的值；‎ ‎（2）分别求出成绩落在中的学生人数；‎ ‎（3）用分层抽样的方法从这200名同学中抽取10人，求样本中成绩在中的学生人数.‎ ‎18．（12分）一个盒子中装有5张编号依次为1，2，3，4，5的卡片，这5张卡片除号码外完全相同，现进行有放回的连续抽取两次，每次任意地取出一张卡片．‎ ‎（1）求出所有可能结果数，并列出所有可能结果；‎ ‎（2）求事件“取出卡片的号码之和不小于7”的概率．‎ ‎19．（12分）已知命题 “任意”，命题：“曲线表示焦点在轴上的椭圆”，命题：“关于的不等式成立”‎ ‎（1）若为真命题，求实数的取值范围；‎ ‎（2）若是的必要不充分条件，求实数的取值范围.‎ ‎20. （12分）中心在原点，焦点在x轴上的一椭圆与一双曲线有共同的焦点F1，F2，且|F1F2|＝，椭圆的长半轴与双曲线实半轴之差为4，椭圆与双曲线的离心率之比为3∶7. ‎ ‎（1）求这两曲线的方程；‎ ‎（2）若P为这两曲线的一个交点，cos∠F1PF2值. ‎ ‎21．（12分）已知双曲线：（）的离心率为．‎ ‎（1）求双曲线的标准方程；‎ ‎（2）过点直线与双曲线相交于两点，为坐标原点，已知的面积为，求直线的斜率.‎ ‎22.（12分）设函数，，其中，为自然对数的底数。‎ ‎（1）讨论的单调性；‎ ‎（2）证明：当时，；‎ ‎（3）确定的所有可能取值，使得在区间内恒成立。‎ 高二期末考试数学试卷（文科）答案 ‎1. C 2. C 3. C 4. B　5. C 6．D 7. A 8．D 9. A 10. D 11． D 12． C ‎13. 0.85 14. －2 15．①③④ 16. .‎ ‎17.解析：（1）由题意，. ‎ ‎（2）成绩落在中的学生人数为，‎ 成绩落在中的学生人数 成绩落在中的学生人数. ‎ ‎（3）落在中的学生为.‎ ‎18．解：（1）盒子中装有5张编号依次为1，2，3，4，5的卡片，这5张卡片除号码外完全相同，‎ 现进行有放回的连续抽取两次，每次任意地取出一张卡片，‎ 基本事件总数n=5×5=25，所有可能结果为：（1，1），（1，2），（1，3），（1，4），（1，5），（2，1），（2，2），（2，3），（2，4），（2，5），（3，1），（3，2），（3，3），（3，4），（3，5），（4，1），（4，2），（4，3），（4，4），（4，5），（5，1），（5，2），（5，3），（5，4），（5，5）．‎ ‎（2）“取出卡片的号码之和不小于7”包含的基本事件有：（2，5），（3，4），（3，5），（4，3），（4，4），（4，5），（5，2），（5，3），（5，4），（5，5），共有m=10个，∴“取出卡片的号码之和不小于7”的概率 ‎19．（1）若为真： 解得 若为真：则 解得 ‎ 若“且”是真命题，则 解得 .‎ ‎（2）若为真，则，即 由是的必要不充分条件，‎ 则可得 即 解得.‎ ‎21. (1)依题意可得，解得，∴双曲线的标准方程为．‎ ‎（2）直线的方程为，由可得，设、,.‎ ‎22.（1） <0，在内单调递减.由=0，有.当时，<0，单调递减；‎ 当时，>0，单调递增.‎ ‎（2）令=，则=.‎ 当时，>0，所以，从而=>0.‎ ‎（3）由（2），当时，>0. 当，时，=.‎ 故当>在区间内恒成立时，必有. 当时，>1.‎ 由（1）有,从而，所以此时>在区间内不恒成立. 当时，令=().‎ 当时，=.‎ 因此在区间单调递增. 又因为=0，所以当时，=>0，即>恒成立. 综上，.‎