数学文卷·2018届甘肃省金昌市永昌县第一中学高二下学期第一次月考(2017-03)
密 线 内 不 准 答 题
班级 姓名 考场号 座位号
永昌县第一高级中学2016—2017—2月考试卷
高二数学 (文科)
本试卷分第Ⅰ卷(选择题 共60分)和第Ⅱ卷(非选择题 共90分),考试时间120分钟,满分为150分。请将第Ⅰ卷正确答案涂在机读卡上,第Ⅱ卷在答题卡上做答。
一、 选择题(每小题5分,共60分)
1.下列三句话按“三段论”模式排列顺序正确的是( )
①y=cos x(x∈R)是三角函数;②三角函数是周期函数;③y=cos x(x∈R)是周期函数.
A.①②③ B.②①③ C.②③① D.③②①
2.在曲线y=x2+1的图象上取一点(1,2)及附近一点(1+Δx,2+Δy),则为( )
A.Δx++2 B.Δx--2 C.Δx+2 D.2+Δx-
3.已知a为函数f(x)=x3-12x的极小值点,则a等于( )
A.-4 B.-2 C.4 D.2
4.2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2 548名男性中有1 560名持反对意见, 2 452名女性中有1 200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.茎叶图 B.分层抽样 C.独立性检验 D.回归直线方程
5.已知f(x)=x3-2x2+x+6,则f(x)在点P(-1,2)处的切线与坐标轴围成的三角形的面积等于( )
A.4 B.5 C. D.
6.函数y=3x-x3的单调递增区间是 ( )
A.(0,+∞) B.(-∞,-1) C.(-1,1) D.(1,+∞)
x
0
1
2
3
y
-1
1
m
8
7.具有线性相关关系的变量x、y的一组数据如下表所示.若y与x的回归直线方程为=3x-,则m的值是( )
A.4 B. C.5.5 D.6
8.若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
A.2 B.3 C.6 D.9
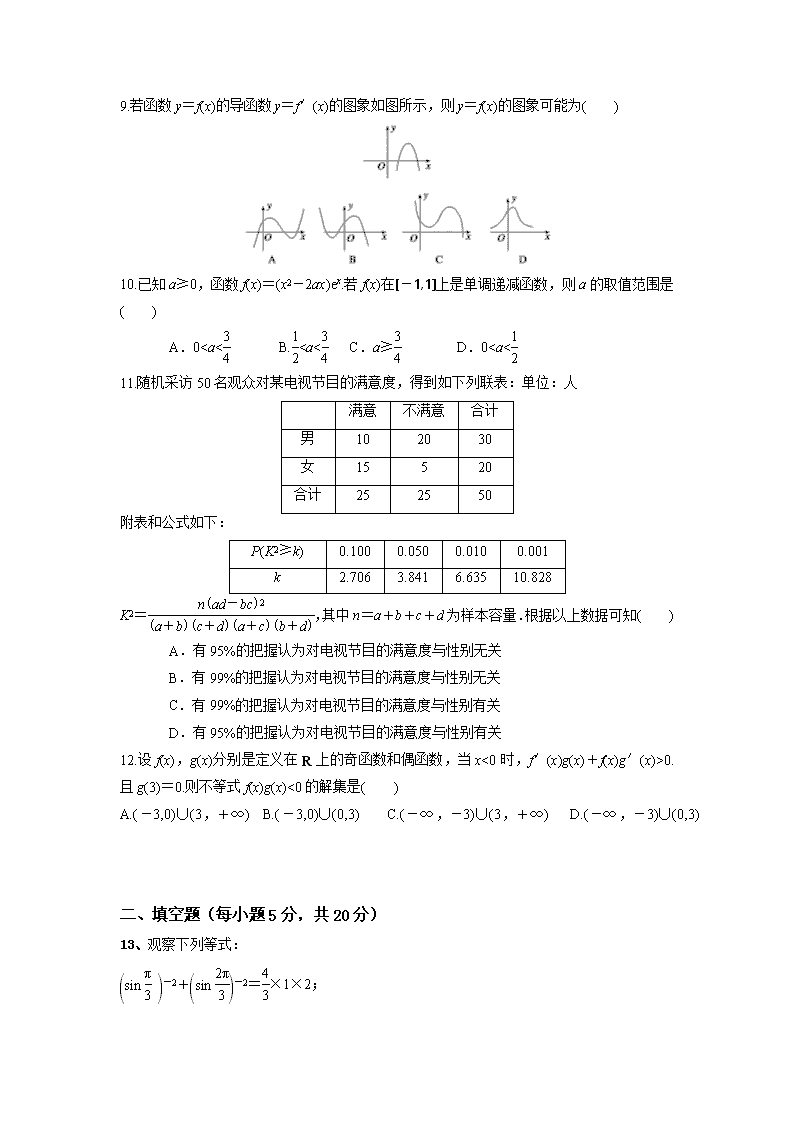
9.若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能为( )
10.已知a≥0,函数f(x)=(x2-2ax)ex.若f(x)在[-1,1]上是单调递减函数,则a的取值范围是( )
A.0
0.且g(3)=0.则不等式f(x)g(x)<0的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3) C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
二、填空题(每小题5分,共20分)
13、观察下列等式:
-2+-2=×1×2;
-2+-2+-2+-2=×2×3;
-2+-2+-2+…+-2=×3×4;
-2+-2+-2+…+-2=×4×5;
…
照此规律,-2+-2+-2+…+-2=__________
14、已知f(x)=(2x-x2)ex,给出以下四个结论:
①f(x)>0的解集是{x|0kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.
一、每小题5分
1、B 2、C 3、 D 4、 C 5、C 6、 C 7、 A
8、 D 9、 C 10、 C 11、 C 12、 D
二、13、;14、①②④;15、(-4,0);16、
三、解答题。
17、(1) (2)
18、解 (1)由题设可知:f′(x)=3x2-6ax-b,f′(1)=0且f(1)=2,
即解得a=,b=-5.
(2)∵f′(x)=3x2-6ax-b=3x2-6ax-9a,
又f(x)在[-1,2]上为减函数,
∴f′(x)≤0对x∈[-1,2]恒成立,
即3x2-6ax-9a≤0对x∈[-1,2]恒成立.
∴f′(-1)≤0且f′(2)≤0,
即⇒⇒a≥1,
∴a的取值范围是a≥1.
19、(1)散点图如图.
(2)由表中数据得:yi=52.5,
=3.5,=3.5,=54,∴ =0.7,∴=1.05,
∴=0.7x+1.05,回归直线如图所示.
(3)将x=10代入线性回归方程,
得=0.7×10+1.05=8.05,
故预测加工10个零件约需要8.05小时.
20、解 设毛利润为L(p),由题意知L(p)=p·Q-20Q=Q(p-20)
=(8 300-170p-p2)(p-20)
=-p3-150p2+11 700p-166 000,
所以L′(p)=-3p2-300p+11 700.
令L′(p)=0,
解得p=30或p=-130(舍去).
此时,L(30)=23 000.
因为在p=30的左侧L′(p)>0,
右侧L′(p)<0,
所以L(30)是极大值,根据实际问题的意义知,L(30)是最大值,即零售价定为每件30元时,毛利润L最大,为23 000元.
21. 解 (1)f′(x)=ex(ax+b)+aex-2x-4
=ex(ax+a+b)-2x-4,
∵y=f(x)在(0,f(0))处的切线方程为y=4x+4,
∴f′(0)=a+b-4=4,f(0)=b=4,
∴a=4,b=4.
(2)由(1)知f′(x)=4ex(x+2)-2(x+2)
=2(x+2)(2ex-1)
令f′(x)=0得x1=-2,x2=ln ,
列表:
x
(-∞,-2)
-2
ln
(ln ,+∞)
f′(x)
+
0
-
0
+
f(x)
极大值
极小值
∴y=f(x)的单调增区间为(-∞,-2),;
单调减区间为.
f(x)极大值=f(-2)=4-4e-2.
22. (1)解 根据题意,得f′(x)=ex-2x,则f′(0)=1=b.
由切线方程可得切点坐标为(0, 0),将其代入y=f(x),
得a=-1,故f(x)=ex-x2-1.
(2)证明 令g(x)=f(x)+x2-x=ex-x-1.
由g′(x)=ex-1=0,得x=0,
当x∈(-∞,0)时,g′(x)<0,y=g(x)单调递减;
当x∈(0,+∞)时,g′(x)>0,y=g(x)单调递增.
∴g(x)min=g(0)=0,∴f(x)≥-x2+x.
(3)解 f(x)>kx对任意的x∈(0,+∞)恒成立等价于>k对任意的x∈(0,+∞)恒成立.
令φ(x)=,x>0,得φ′(x)=
==.
由(2)可知,当x∈(0,+∞)时,ex-x-1>0恒成立,
令φ′(x)>0,得x>1;令φ′(x)<0,得0
查看更多