2017-2018学年重庆长寿中学高二下学期第三次月考数学（文）试题 Word版

2017-2018学年重庆长寿中学高二下学期第三次月考数学（文）试题 Word版

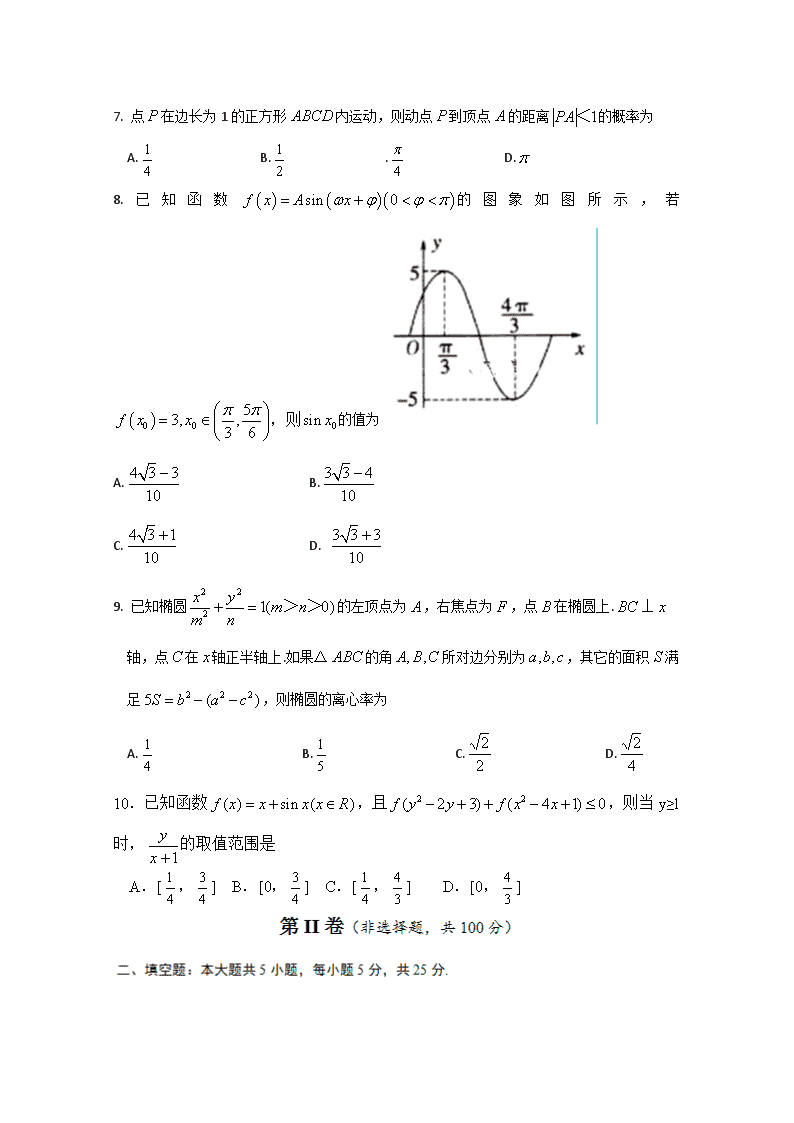
‎2017-2018学年重庆长寿中学高二下学期第三次月考 数学试题（文科）‎ ‎ ‎ ‎ 本试卷分第I卷（选择题）和第II卷（非选择题）两部分。‎ ‎1．已知集合,则等于 A．{-1,0,1} B．{1} C．{-1,1} D．{0,1}‎ 2. 复数的共轭复数是 ‎ ‎ A. B. C. D.‎ ‎3.已知实数x，y满足约束条件，则的最小值是（ ）.‎ ‎ (A) 5 (B) -6 (C) 10 (D) -l0‎ ‎4．下列命题中的假命题是（ ）‎ A. B.‎ C D.‎ ‎5.如图所示的三棱柱，其正（主）视图是一个边长为2的正方形，俯视图是一个正三角形，则该三棱柱侧（左）视图的面积为 A. B. C. D.4‎ ‎6．某程序框图如图所示，则该程序运行后输出的值是 A． B． C． D．‎ ‎7. 点在边长为1的正方形内运动，则动点到顶点的距离的概率为 ‎ ‎ A. B. . D.‎ ‎8.已知函数的图象如图所示，若的值为 A. B.‎ C. D. ‎ 9. 已知椭圆的左顶点为，右焦点为，点在椭圆上.⊥‎ ‎ 轴，点在轴正半轴上.如果△的角所对边分别为，其它的面积满 ‎ 足，则椭圆的离心率为 ‎ A. B. C. D.‎ ‎10．已知函数，且，则当y≥l时，的取值范围是 A．[，] B．[0，] C．[，] D．[0，]‎ 11． 一组样本数据的茎叶图如右：，则这组数据的平均数等于 .‎ ‎12.已知幂函数的图像经过点，则_________.‎ 13. 已知是两个单位向量，且，若的夹角为60°则实数__‎ ‎14．已知椭圆方程为，、分别是椭圆长轴的两个端点，、是椭圆上关于x轴对称的两点，直线的斜率分别为，若，则椭圆的离心率为 ．‎ ‎15. 定义一个对应法则．现有点与，点是线段上一动点，按定义的对应法则．当点在线段AB上从点A开始运动到点B结束时，点M的对应点所经过的路线长度为 ．‎ ‎ 16.（本小题13分）某网站针对“2014年法定节假日调休安排”展开的问卷调查，提出了A、B、C三种放假方案，调查结果如下：‎ 支持A方案 支持B方案 支持C方案 ‎35岁以下 ‎200‎ ‎400‎ ‎800‎ ‎35岁以上（含35岁）‎ ‎100‎ ‎100‎ ‎400‎ ‎（1）在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持A方案”的人中抽取了6人，求n的值；‎ ‎（2）在“支持B方案”的人中，用分层抽样的方法抽取5人看作一个总体，从这5人中任意选取2人，求恰好有1人在35岁以上（含35岁）的概率.‎ ‎17. （本小题13分） 已知函数，直线与的图象交点之间的最短距离为．‎ ‎（1）求的解析式及其图象的对称中心；‎ ‎（2）设的内角的对边分别为，若，，求的面积.‎ ‎18.（本小题满分13分）‎ 如图所示，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面底面ABCD，且，若E,F分别为PC,BD的中点. ‎ ‎（I）求证：EF//平面PAD；‎ ‎（II）求三棱锥F-DEC的体积；‎ ‎（III）在线段CD上是否存在一点G，使得平面平面PDC？若存在，请说明其位置，并加以证明；若不存在，请说明理由.‎ ‎19. (本题12分)己知各项均为正数的数列{}满足(N*),且是的等差中项。‎ ‎(I)求数列{}的通项公式；‎ ‎(II)若，求使成立的正整数n的最小值．‎ ‎20.（本小题12分）已知函数.‎ ‎（Ⅰ）若时，求曲线在点处的切线方程；‎ ‎（Ⅱ）设若存在对于任意使 求的取值范围．‎ ‎21.（本小题12分）已知椭圆的离心率为，过焦点且垂直于长轴的直线被椭圆截得的弦长为，过点的直线与椭圆相交于两点 ‎（1）求椭圆的方程；‎ ‎（2）设为椭圆上一点，且满足（为坐标原点），当时，求实数的取值范围．‎ 数学测试题（文科）‎ 答案：BCBCC DCDBA ‎11.23 12. 13. 1 14. 15. ‎ ‎16.‎ 共10种.‎ 其中满足条件得有4种.故. ‎ 答：恰好有1个人在35岁以上（含35岁）的概率为. ……12分 ‎17. 解：（1）‎ ‎ 由题可知，‎ ‎ ,对称中心 ‎ （2）‎ ‎ 又 或 ‎ ‎ 当时：由余弦定理，‎ ‎ ‎ ‎ 同理，当时： 故 ， 或 ‎20. 解：‎ ‎ ‎ ‎（Ⅰ）当，；‎ 故在点处的切线方程为：，即; ‎ ‎（Ⅱ）当 ‎ ，‎ ‎ ，则,‎ ‎ 因此，当时，一定符合题意; ‎ 当令 ‎ ‎ 所以，当 ‎ ‎ ‎ 由题意知，只需满足 ‎ ‎ 综上： ‎ 实数的取值范围．‎ ‎21.解（1） 由已知，所以，所以 所以 …… 1分 ‎ 又由过焦点且垂直于长轴的直线被椭圆截得的弦长为 所以 …… 3分 ‎ 所以 …… 4分 ‎（2）设 ‎ ‎ 设与椭圆联立得 ‎ ‎ ‎ 整理得 ‎ ‎ ‎ 得 …… 6分 ‎ ‎ ‎ ‎ ‎ ‎ 由点在椭圆上得 ‎ ‎ …… 8分 ‎ ‎ 又由, 所以 ‎ ‎ ‎ ‎ ‎ ‎ ‎ 所以 …… 11分 ‎ ‎ 所以 由得 ‎ ‎ ‎ 所以，所以或 …… 13分