上学期期中考试高二数学(文科)试题及答案1

上学期期中考试高二数学(文科)试题及答案1

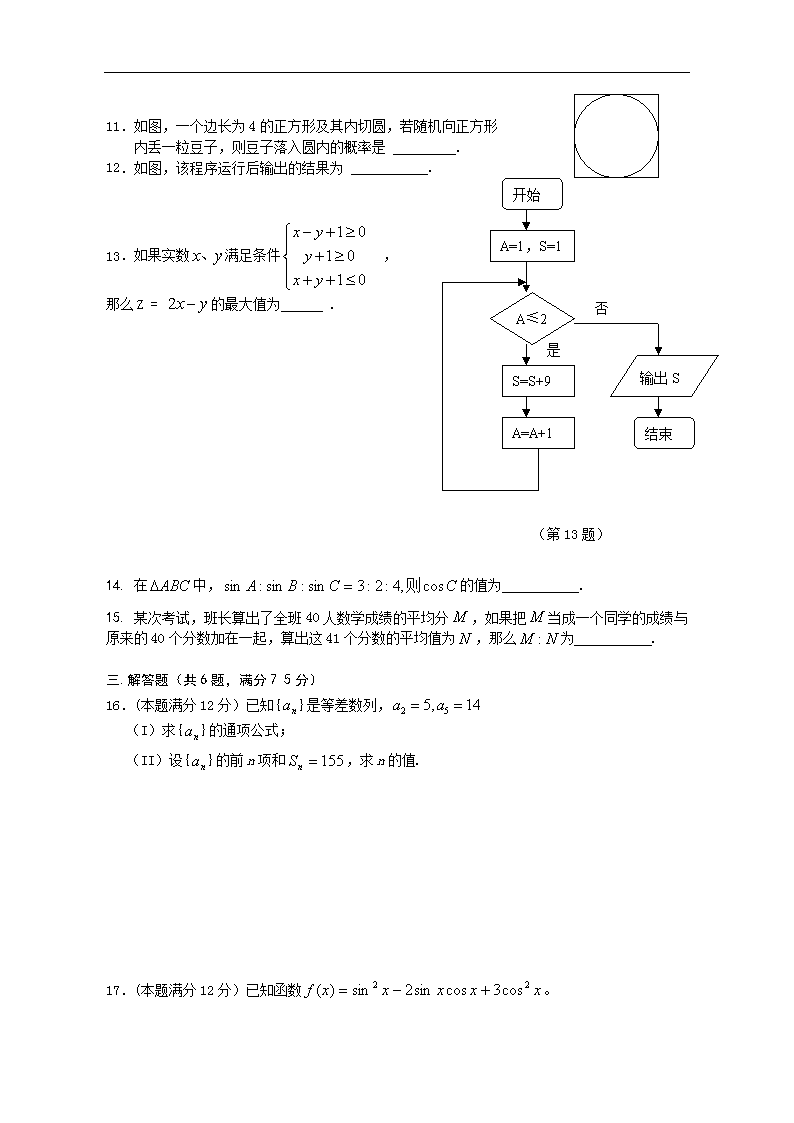
‎2017年上学期期中考试高二数学（文科）试题及答案 时量：120分钟 分值：150分 ‎ 一、 选择题（每小题5分，共45分）‎ ‎1．已知集合，，则的元素个数是( )‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎2． ( )‎ A．cos30o B． C． D．‎ ‎3．直线与圆没有公共点，则的取值范围是( )‎ A．　 B．　 C． D． ‎ ‎4．采用系统抽样从个体数为83的总体中抽取一个样本容量为10的样本，那么每个个体被抽取的概率为（ ） ‎ A．8 B. 8.3 C． D. ‎ ‎5．已知点A（1，2）与B（3，4），则线段AB的垂直平分线方程为（ ）．‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎6．在等差数列｛a｝中，已知a= 2, a+ a=13，则a+ a + a等于( )‎ A.40 B.42 C.43 D.45 ‎ ‎7．有一个几何体的三视图及其尺寸如下（单位cm），则该几何体的体积为： ‎ ‎6‎ ‎5‎ 俯视图 主视图 侧视图 A.12πcm3 B.15πcm2 C.36πcm3 D.以上都不正确 ‎8．在算式4×□＋△=30的□、△中，分别填入一个正整数使算式成立，并使它们的倒数之和最小，则这两个数构成的数对（□、△）应为（ ）‎ ‎ A．（4，14） B．（6，6） C．（3，18） D．（5，10）‎ ‎9．从盛满20升纯酒精的容器里倒出1升，然后用水加满，再倒出1升混合溶液，再用水加满. 这样继续下去，建立所倒次数和酒精残留量之间的函数关系( )‎ A. B. C. D.‎ 二、 填空题（每小题5分，共30分）‎ ‎10．若, ,且,则与的夹角是 . ‎ ‎11．如图，一个边长为4的正方形及其内切圆，若随机向正方形 内丢一粒豆子，则豆子落入圆内的概率是 .‎ ‎12．如图，该程序运行后输出的结果为 .‎ A=1，S=1‎ S=S+9‎ A=A+1‎ A≤2‎ 输出S 结束 开始 是 否 ‎ ‎ ‎ ‎ ‎13．如果实数满足条件 ，‎ 那么Z = 的最大值为 .‎ ‎（第13题）‎ ‎14. 在中，的值为 .‎ ‎15. 某次考试，班长算出了全班40人数学成绩的平均分，如果把当成一个同学的成绩与原来的40个分数加在一起，算出这41个分数的平均值为，那么为 .‎ 三.解答题（共6题，满分7 5分）‎ ‎16．(本题满分12分）已知{}是等差数列，‎ ‎ （I）求{}的通项公式；‎ ‎ （II）设{}的前n项和，求n的值. ‎ ‎17．(本题满分12分）已知函数。‎ ‎（1）求的最小正周期；（2）求的最大值和最小值，以及取得最大值时x的值。‎ ‎ ‎ ‎18. (本题满分12分）已知点A(1,-1),B(5,1),直线经过点A,且斜率为，‎ ‎ （1）求直线的方程。（2）求以B为圆心，并且与直线相切的圆的标准方程。‎ ‎ ‎ ‎ ‎ ‎19．(本题满分13分）如图,在底面为平行四边形的四棱锥P－ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点. ‎ ‎（1）求证：AC⊥PB；（2）求证：PB∥平面AEC；‎ ‎ ‎ ‎20. (本题满分13分）电信局为了配合客户不同需要，设有A、B两种方案，这两种方案应付话费（元）与通话时间（分钟）之间的关系如图所示（MN//CD）.‎ ‎ （Ⅰ）若通话时间为250分钟，按方案A、B各付话费多少元？‎ ‎ （Ⅱ）方案B从500分钟以后，每分钟收费多少元？‎ ‎ （Ⅲ）通话时间在什么范围内方案B才会比方案A优惠？‎ ‎21．(本题满分13分）已知函数，若对任意，且，都有． ‎ ‎（Ⅰ）求实数的取值范围；‎ ‎（Ⅱ）对于给定的实数，有一个最小的负数，使得时，都成立，则当为何值时，最小，并求出的最小值．‎ ‎2017年上学期期中考试高二数学（文科）试题答案 一. 选择题: BADCB,BADA.‎ 二.填空题: 10. 45O; 11. ; 12. 19; 13.1 14. 15.1‎ 三.解答题:‎ ‎16.（Ⅰ）解：设等差数列 则 ……………………2分 解得 …………………………4分 所以数列的通项为……………………6分 ‎ （Ⅱ）数列的前n项和…………………………9分 由 即 所以……………………………………12分 ‎ ‎ ‎ 17.‎ ‎ ‎ ‎18. 解：由直线方程点斜方程：‎ ‎　直线过Ａ点：即，‎ 整理得：3x+4y+1=0‎ ‎(2)由题意，与圆Ｂ相切，则圆心Ｂ与直线的距离为圆的半径。‎ 则：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ 以Ｂ为圆心的圆的标准方程：　‎ ‎19.解:1）证明：∵PA⊥平面ABCD ‎ 即AB是PB在面ABCD上的射影 ………2分 ‎　又∵AB⊥AC ………4分 ‎ ‎ ∴AC⊥PB ………………………6分 ‎2）证明：连结BD交AC于O，连结EO ………………7分 ‎∵平行四边形ABCD ∴O为BD中点 ………………8分 又∵E为PD中点∴EO∥PB …………10分 又∵PB不在平面AEC中,EO在平面AEC中 …………12分 ‎∴PB∥平面AEC …………13分 ‎20.解：由图知M（225，38），C（500，68），N（500，148）‎ ‎ ‎ 设这两种方案的应付话费与通话时间的函数关系式分别为、，‎ 则 ‎………………………………4分 ‎ （Ⅰ）通话时间为250分钟时，方案A、B的费和分别为（元），68元.……………………………………………………………………6分 ‎ （Ⅱ）由直线CD的斜率的实际意义知方案B从500分钟以后每分钟收费0.4元.…8分 ‎ （Ⅲ）由图知：当当时，‎ 当即 则，‎ 故当时，方案B较优惠.………………………………13分 ‎21.解：（Ⅰ）∵‎ ‎， ……2分 ‎∵，∴．‎ ‎∴实数的取值范围为． ……4分 ‎（Ⅱ）∵， ‎ 显然，对称轴． ……6分 ‎（1）当，即时，，且．‎ 令，解得，‎ 此时取较大的根，即，‎ ‎∵，∴． ……10分 ‎（2）当，即时，，且．‎ 令，解得，‎ 此时取较小的根，即，‎ ‎∵，∴． ……12分 当且仅当时，取等号．‎ ‎∵，‎ ‎∴当时，取得最小值－3． ……13分