数学文卷·2018届内蒙古集宁一中西校区高三第三次月考（2017

数学文卷·2018届内蒙古集宁一中西校区高三第三次月考（2017

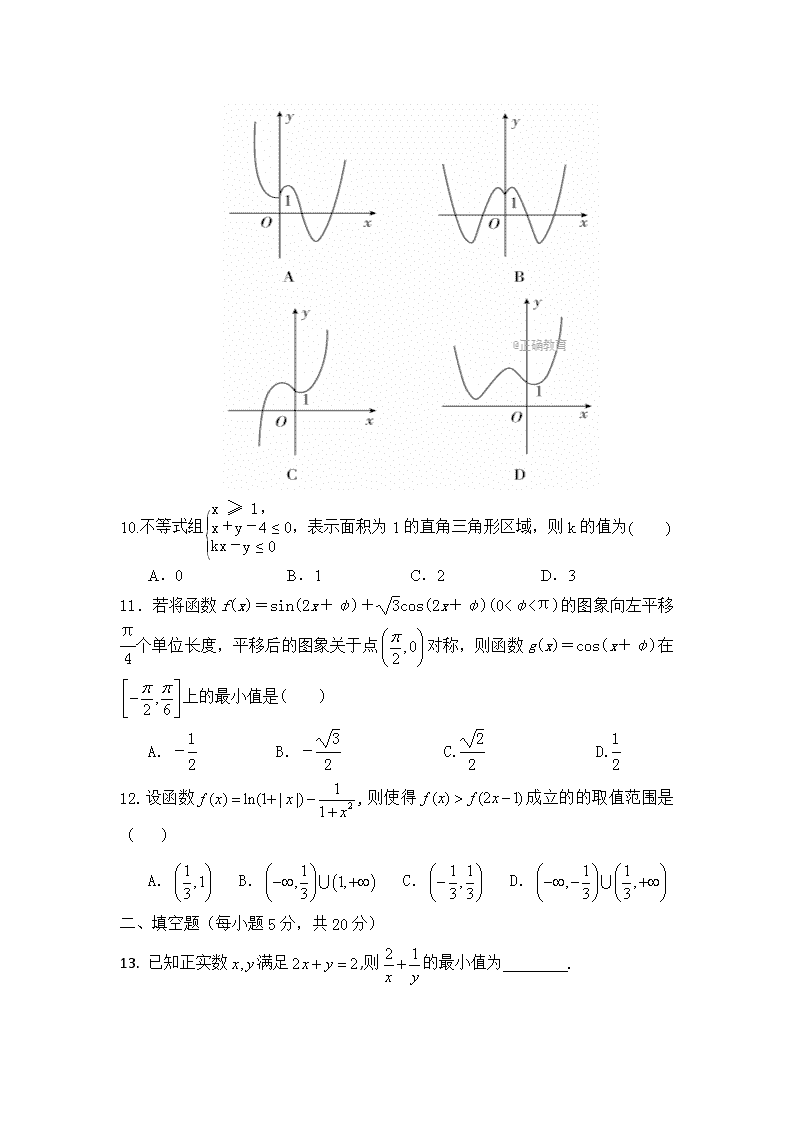
集宁一中2017-2018学年第一学期第三次月考 高三年级文科数学试题 本试卷满分为150分，考试时间为120分钟。 ‎ 第Ⅰ卷（选择题 共60分）‎ 一、 选择题（在下列各题的四个选项中，只有一个是最符合题意的。每小题5分，‎ 共60分。）‎ ‎1．已知集合，则( )‎ A. B. C. D.‎ ‎2. 已知i为虚数单位，复数z的共轭复数为，且满足2z+= 3-2i，则z=( )‎ A．l-2i B．l+2i C．2-i D．2+i ‎3.已知向量,,且，则的值为（ ） ‎ A． B． C． D．‎ ‎4．直线y＝kx＋2与圆x2＋y2＝1没有公共点的充要条件是(　　)‎ A．k∈(－，) B．k∈(－∞，－)∪(，＋∞)‎ C．k∈(－，) D．k∈(－∞，－)∪(，＋∞)‎ ‎5.若， ， ，则（ ）‎ A. B. C. D. ‎ ‎6.函数的单调递增区间是（ ）‎ A． B． C． D． ‎ ‎7.已知P是△ABC所在平面外的一点，M、N分别是AB、PC的中点，若MN＝BC＝4，PA＝4，则异面直线PA与MN所成角的大小是(　　)‎ A．30° B．45° C．60° D．90°‎ ‎8．设F1，F2分别是椭圆＋＝1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|＝3，则P点到椭圆左焦点的距离为(　　)‎ A．4　　　 　B．3　　　　 C．2　　　 　D．5‎ ‎9．函数y＝e|x|－x3的大致图象是(　　)‎ ‎10.不等式组表示面积为1的直角三角形区域，则k的值为(　　)‎ A．0 B．1 C．2 D．3‎ ‎11．若将函数f(x)＝sin(2x＋φ)＋cos(2x＋φ)(0<φ<π)的图象向左平移个单位长度，平移后的图象关于点对称，则函数g(x)＝cos(x＋φ)在上的最小值是(　　)‎ A．－ B．－ C. D. ‎12.设函数,则使得成立的的取值范围是（ ）‎ A． B． C． D．‎ 二、填空题（每小题5分，共20分）‎ ‎13. 已知正实数满足,则的最小值为 .‎ ‎14. 已知则的值为 .‎ ‎15. 直线与圆相交于A、B两点，则 .‎ ‎16. 已知函数若存在实数b，使得关于x的方程f（x）=b有三个不同的根，则m的取值范围是 ‎ 三、解答题（17题10分，18-22题，每题12分，共70分）‎ ‎17.（本小题满分10分）已知在中，角所对的边分别为已知 ‎（Ⅰ）求的值；‎ ‎（Ⅱ）若,求的面积 ‎18.（本小题满分12分）已知数列的首项为，且.‎ ‎（Ⅰ）求证：数列是等比数列，并求数列的通项公式；‎ ‎（Ⅱ）若，求数列的前项和.‎ ‎19.（本小题满分12分）如图，在四棱锥中，侧棱底面，底面为矩形，，为上一点，且.‎ ‎（1）若为的中点，求证：平面；‎ ‎（2）求三棱锥的体积.‎ ‎20.（本小题满分12分）已知点P(2,2)，圆C：x2＋y2－8y＝0，过点P的动直线l与圆C交于A，B两点，线段AB的中点为M，O为坐标原点。‎ ‎(1)求M的轨迹方程；‎ ‎(2)当|OP|＝|OM|时，求l的方程及△POM的面积．‎ ‎21．(本小题满分12分)已知椭圆C的焦点坐标是F1(－1,0)、F2(1,0)，过点F2垂直于长轴的直线l交椭圆C于B、D两点，且|BD|＝3.‎ ‎(1)求椭圆C的方程；‎ ‎(2)是否存在过点P(2,1)的直线l1与椭圆C相交于不同的两点M、N，且满足·＝？若存在，求出直线l1的方程；若不存在，请说明理由．‎ ‎22. (本小题满分12分)已知函数，函数，函数的导函数为.‎ ‎（1）求函数的极值；‎ ‎（2）若，‎ ‎（i）求函数的单调区间；‎ ‎（ii）求证：时，不等式恒成立.‎ 集宁一中2017-2018学年第一学期第三次月考 高三年级文科数学试题答案 选择题：1-6CABCAD 7-12AAABDA ‎13. 14. 15.2 16. ‎ ‎17、(12分)【答案】（Ⅰ）;(Ⅱ).‎ ‎（Ⅰ）因为所以所以 又故,故,由正弦定理可得 ‎(Ⅱ)由（Ⅰ）可得，联立,解得.由，得为直角三角形,所以 ‎18．解：（Ⅰ）由得， …………2分 则数列是以3为首项，以2为公比的等比数列， …………4分 可得，从而. …………6分 ‎（Ⅱ）依题意，， …………8分 故， …………9分 故. …………12分 ‎19.解：（1）连结BD交AC于O，连结OE，‎ ‎∵为的上一点，且，‎ 又 ∵F为PE的中点， ‎ ‎∴E为DF中点，OE//BF ，‎ ‎ 又∵平面AEC ∴平面AEC ‎（2）侧棱底面，，‎ 又，，‎ ‎∴， ‎ 又,‎ ‎∴‎ ‎20.解析：(1)圆C的方程可化为x2＋(y－4)2＝16，所以圆心为C(0,4)，半径为4。‎ 设M(x，y)，则＝(x，y－4)，＝(2－x,2－y)。‎ 由题设知·＝0，故x(2－x)＋(y－4)(2－y)＝0，即(x－1)2＋(y－3)2＝2。‎ 由于点P在圆C的内部，所以M的轨迹方程是(x－1)2＋(y－3)2＝2。‎ ‎(2)由(1)可知M的轨迹是以点N(1,3)为圆心，为半径的圆。‎ 由于|OP|＝|OM|，故O在线段PM的垂直平分线上，又P在圆N上，从而ON⊥PM。‎ 因为ON的斜率为3，所以l的斜率为－，故l的方程为y＝－x＋。‎ 又|OM|＝|OP|＝2，O到l的距离为，|PM|＝，所以△POM的面积为。‎ ‎21.解　(1)设椭圆的方程是＋＝1(a>b>0)，则c＝1，‎ ‎∵|BD|＝3，∴＝3，又a2－b2＝1，∴a＝2，b＝，‎ ‎∴椭圆C的方程为＋＝1.(4分)‎ ‎(2)假设存在直线l1且由题意得斜率存在，设满足条件的方程为y＝k(x－2)＋1，‎ 由得(3＋4k2)x2－8k(2k－1)x＋16k2－16k－8＝0，‎ 因为直线l1与椭圆C相交于不同的两点M、N，设M(x1，y1)、N(x2，y2)，‎ 所以Δ＝[－8k(2k－1)]2－4(3＋4k2)(16k2－16k－8)>0，所以k>－.‎ 又x1＋x2＝，x1x2＝，(8分)‎ 因为·＝(x1－2)(x2－2)＋(y1－1)(y2－1)＝，‎ 所以(x1－2)(x2－2)(1＋k2)＝，即[x1x2－2(x1＋x2)＋4](1＋k2)＝，‎ 所以(1＋k2)＝＝.‎ 解得k＝±，因为k>－，所以k＝.‎ 故存在直线l1满足条件，其方程为y＝x.(12分)‎ ‎22.解：（1）∵，∴，‎ ‎∴，或，‎ ‎∴上，；上；上.‎ ‎∴的极小值为；函数的极大值为.‎ ‎（2）∵，∴，.‎ ‎（i）记，，‎ 在上，，是减函数；在上，，是増函数，‎ ‎∴，则在上，；在上，，‎ 故函数的单调递增区间是，单调递减区间是.‎ ‎（ii）时，，‎ 由（i）知，.‎ 记，则，‎ 在区间上，，是增函数；在区间上，，是减函数，‎ ‎∴，∴，∴，‎ ‎∴，即成立.‎