广东省2020届高三数学文一轮复习典型题专项训练：三角函数

广东省2020届高三数学文一轮复习典型题专项训练：三角函数

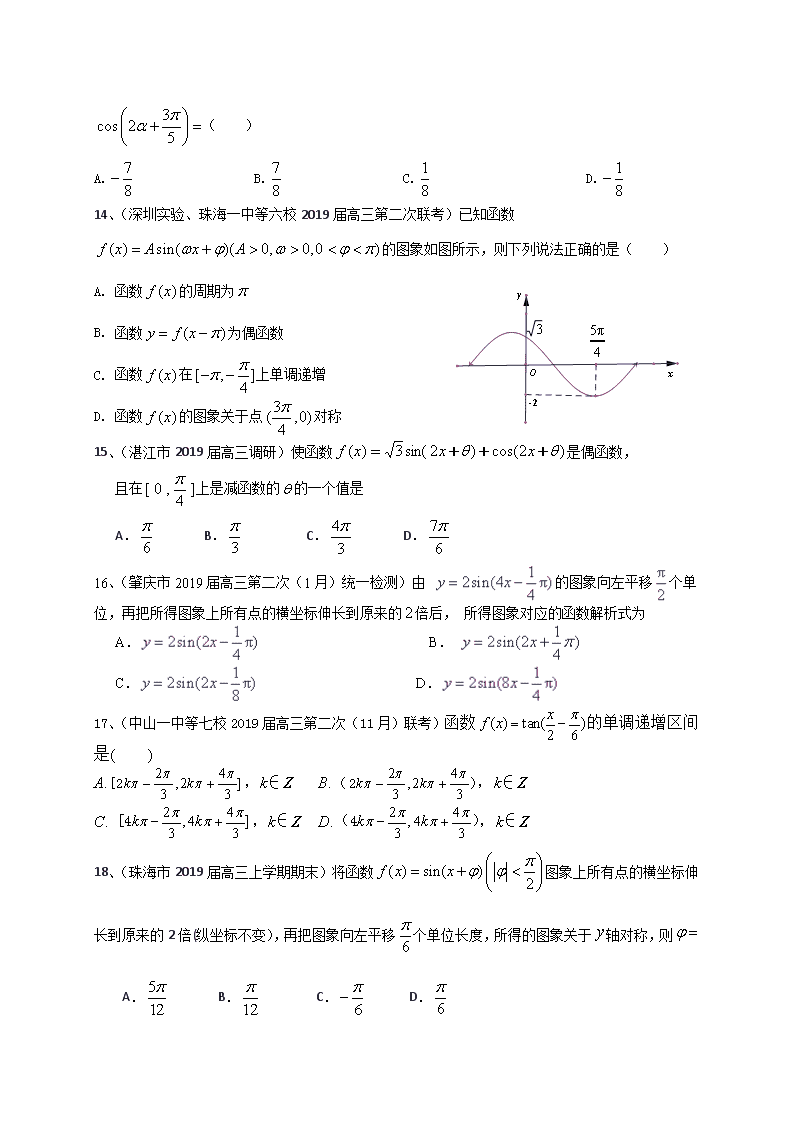
广东省2020届高三数学文一轮复习典型题专项训练 三角函数 一、选择、填空题 ‎1、（广州市2018届高三3月综合测试（一））已知函数在区间上单调递增，则的取值范围为 A． B． C． D．‎ ‎2、（深圳实验、珠海一中等六校2019届高三第一次联考）将函数的图象向右平移个单位后得到函数，则具有性质( )‎ ‎ A．最大值为1，图象关于直线对称 B．在上单调递增，为奇函数 ‎ C．在上单调递增，为偶函数 D．周期为π，图象关于点对称 ‎3、（深圳市宝安区2019届高三9月调研）已知，则 ‎ ‎4、（仲元中学等七校2019届高三第一次（8月）联考）函数在一个周期内的图像是（ ）‎ A. B. ‎ C. D. ‎ ‎5、（广州市2019届高三3月综合测试（一））若，则下列不等式中一定成立的是 A . B.‎ C. D. ‎ ‎6、（广州市2019届高三12月调研）由的图象向左平移个单位，再把所得图象上所有点的横坐标伸长到原来的2倍后， 所得图象对应的函数解析式为 ‎ A． B． ‎ ‎ C． D．‎ ‎7、（惠州市2019届高三4月模拟）设函数的图象为，下面结论中正确的是（ ）‎ A． 函数的最小正周期是． B．图象关于直线对称．‎ C． 图象可由函数的图象向右平移个单位得到．‎ D． 图象可由函数的图象向左平移个单位得到．‎ ‎8、（惠州市2019届高三第二次（10月）调研）已知，，则（ ）‎ A． B． C． D．‎ ‎9、（江门市 2019届普通高中高三调研）函数的最小正周期和最大值是 A．，1 B．，‎1 C．， D．，‎ ‎10、（揭阳市2019届高三学业水平考试）已知，且，则=‎ A． B． C． D．2 ‎ ‎11、（雷州市2019届高三上学期期末）若，则 A. B. C. D. ‎ ‎12、（汕头市2019年普通高考第一次模拟）将函数的图象向右平移个单位长度，得到函数的图象，则在上的最大值为（ ）‎ ‎ A． B． C． D．1‎ ‎13、（深圳实验、珠海一中等六校2019届高三第二次联考）已知，则 ‎（ ）‎ A. B. C. D.‎ ‎14、（深圳实验、珠海一中等六校2019届高三第二次联考）已知函数的图象如图所示，则下列说法正确的是（ ） ‎ A. 函数的周期为 ‎ B. 函数为偶函数 C. 函数在上单调递增 ‎ D. 函数的图象关于点对称 ‎15、（湛江市2019届高三调研）使函数是偶函数，‎ 且在上是减函数的的一个值是 A． B． C． D．‎ ‎16、（肇庆市2019届高三第二次（1月）统一检测）由 的图象向左平移个单位，再把所得图象上所有点的横坐标伸长到原来的倍后， 所得图象对应的函数解析式为 ‎ A． B． ‎ ‎ C． D．‎ ‎17、（中山一中等七校2019届高三第二次（11月）联考）函数的单调递增区间是(　　) ‎ A.，k∈Z B. ，k∈Z ‎ C. ，k∈Z D. ，k∈Z ‎18、（珠海市2019届高三上学期期末）将函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变），再把图象向左平移个单位长度，所得的图象关于轴对称，则 A． B． C． D． ‎ ‎19、（佛山市2019届高三教学质量检测（一））在△ABC中，D是边AC上的点，且AB＝AD，2AB＝BD，sinC＝，则＝（　　）‎ A． B． C．2 D．3‎ ‎20、（深圳市宝安区2019届高三9月调研）函数的图象在上恰有两个最大值点，则的取值范围为（ ）‎ A． B． C． D．‎ ‎21、（广州市2019届高三3月综合测试（一））函数最大值是 ‎ A.2 B. C. D.‎ ‎22、（广州市2019届高三3月综合测试（一））△ABC的内角A，B，C的对边分别为a，b，c，已知b=2，c=3，C=2B，则△ABC的面积为 。‎ ‎23、（广州市2019届高三12月调研）设为第二象限角，若，则 = ．‎ ‎24、（惠州市2019届高三第二次（10月）调研）已知，，则的值为（ ）‎ A. B. C. D.或 ‎25、（雷州市2019届高三上学期期末）在△ABC中，角A、B、C所对的边分别为、、，若，则A . ‎ ‎26、（湛江市2019届高三调研）若的内角、、满足，则的最小值是 ．‎ ‎27、（肇庆市2019届高三第二次（1月）统一检测）已知，则 ．‎ 若则 A． B． C． D． ‎ ‎28、（珠海市2019届高三上学期期末）若则 A． B． C． D． ‎ ‎29、（佛山市2019届高三教学质量检测（一））已知函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）两条相邻对称轴为x＝和x＝，若f（0）＝，则f（）＝（　　）‎ A．﹣ B．﹣ C． D．‎ 参考答案：‎ 一、选择、填空题 ‎1、B　　2、B　　　3、　　　4、B　　　5、D ‎6、A　　　7、B　　　8、B　　　9、C　　　10、B ‎11、C　　　12、C　　　13、A　　　14、C　　　15、B ‎16、A　　　17、B　　　18、A 19、C　　20、C ‎21、C　　　22、　　23、　　24、B　　　25、‎ ‎26、．提示：依题意由正弦定理可得：，‎ ‎ （当且仅当 时取等号）．‎ ‎27、　　　28、C　　29、C 二、解答题 ‎1、（广州市2018届高三3月综合测试（一））△的内角，，的对边分别为，，，已知，，△的外接圆半径为．‎ ‎（1）求角的值；‎ ‎（2）求△的面积．‎ ‎2、（深圳实验、珠海一中等六校2019届高三第一次联考）在中，内角所对的边分别为，已知．‎ ‎（Ⅰ）求角的大小；‎ ‎（Ⅱ）若的面积，且，求．‎ ‎3、（惠州市2019届高三4月模拟）在中，内角、、的对边分别为、、，且．‎ ‎（1）求的值；‎ ‎（2）若，，求的面积．‎ ‎4、（惠州市2019届高三第二次（10月）调研）已知函数（，，）的部分图象如图所示．‎ ‎（1）求函数的解析式；‎ ‎（2）将图象上所有点向右平移个单位长度，得到的图象，求的图象的对称中心．‎ ‎5、（惠州市2019届高三第二次（10月）调研）在中，是内角的对边，且， ．‎ ‎（1）求边的值；‎ ‎（2）求周长的最大值．‎ ‎6、（江门市 2019届普通高中高三调研）△的角、、所对的边分别为、、，．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）若△外接圆的半径，求△面积的最大值．‎ ‎7、（揭阳市2019届高三学业水平考试）在中，内角、、所对的边分别是、、，且，‎ ‎（1）求；‎ ‎（2）当函数取得最大值时，试判断的形状．‎ ‎8、（汕头市2019年普通高考第一次模拟）在 DABC 中，角 A，B，C 的对边分别为 a，b，c，b sin A = a(2 - cos B) .‎ ‎(1)求角 B 的大小；‎ ‎(2) D 为边 AB 上一点， 且满足CD = 2，AC = 4 ，锐角三角形 DACD的面积为， 求BC的长。‎ ‎9、（惠州市2018届高三4月模拟考试）已知,,分别为△三个内角,,的对边，且.‎ ‎（1）求角的大小；‎ ‎（2）若,且△的面积为,求的值.‎ ‎10、（惠州市2018届高三第三次调研）在中，角的对边分别为，已知.‎ ‎（1）求；‎ ‎（2）若， 边上的中线，求的面积.‎ ‎11、（揭阳市2018届高三学业水平（期末））在中,内角、、所对的边分别为、、，已知．‎ ‎（Ⅰ）求角的大小；‎ ‎（Ⅱ）已知的周长为，面积为,求最长边的长度．‎ 参考答案：‎ 二、解答题 ‎1、‎ ‎2、解：（Ⅰ）∵，‎ ‎∴，‎ 于是，……1分 由正弦定理得，……2分 即 ……3分 ‎∵，‎ ‎∴，即，……4分 ‎∵，∴，∴ ……5分 ‎∵，∴． ……6分 ‎（Ⅱ）∵，∴，……7分 ‎∵，∴ ，……8分 ‎∴，即，（或求出） ……10分 ‎ ……11分 ‎ ……12分 ‎3、（1）【解法一】由正弦定理得，…………1分 ，；…………2分 ‎，…………3分 ‎，…………4分 ‎，…………5分 ‎…………6分 ‎（1）【解法二】由余弦定理得…………1分 化简得，…………2分 ‎…………4分 ‎，…………5分 ‎…………6分 ‎（2）由，，得，…………7分 在中，，……9分 由正弦定理，得，…………11分 ‎…………12分 ‎4、【解析】（1）由图形可得，…………1分 ‎，解得.…………3分 过点，，即（），‎ ‎（）.又， .…………5分 ‎.…………6分 ‎（2）由（1）知，‎ 则 .…………8分 令（），解得（），…………10分 所以的对称中心为（）. …………12分 ‎5、【解析】(1)由得.…………1分 ‎∴,即.…………2分 由正弦定理得,故.…………4分 ‎(2)解法1、由余弦定理得.…………6分 ‎…………10分 所以当时, 的周长的最大值为.…………12分 解法2、…………5分 由正弦定理得，…………6分 ‎ ‎ ‎…………7分 ‎…………8分 ‎…………9分 ‎ ‎ ‎，即的周长的最大值为。…………12分 ‎6、（Ⅰ）由余弦定理 ， ……1分 得 ……2分 ‎ ……3分 ‎，所以 ……5分 ‎（方法二）由正弦定理 ，， ……1分 得 ……2分 ‎，所以 ……3分 ‎，所以 ……5分 ‎（Ⅱ）由正弦定理 ， ……6分 ‎△的面积 ……8分 ‎ ‎ ‎ ……10分 ‎，， ……11分 所以，△面积的最大值为 ……12分 ‎7、解：（1）由正弦定理得，----------------------------------2分 又,‎ ‎∴,即，------------------------------------------------------------------------4分 ‎∵ ∴.-----------------------------------------------------------------------------6分 ‎（2）解法一：∵ ∴,从而， ------------------------------7分 ‎∴------------------------------------------8分 ‎---------------------------------------------10分 ‎ ∵,∴当时，函数取得最大值，‎ 这时,即是直角三角形. -------------------------------------------12分 ‎【解法二：∵ ∴, -----------------------------------------------------------------7分 ‎∴‎ ‎--------------------------------------------------------------------------------------10分 ‎∵,∴当时，函数取得最大值，‎ ‎∴是直角三角形.------------------- --------------------------------------------------------12分】‎ ‎8、‎ ‎9、【解析】（Ⅰ）由正弦定理得： …………2分 由于 ，∴ ，∴ ‎ 即 …………4分 ‎∵，∴ ‎ ‎∴ ‎ ‎∴ …………6分 ‎（Ⅱ）由： 可得 ∴ …………8分 由余弦定理得： …………10分 ‎∴ …………12分 ‎10、【解析】试题分析：（1）将代入化简求值即可；（Ⅱ）在中，由余弦定理解 得或6，利用面积公式求解即可.‎ 试题解析：‎ ‎（1）由已知得 ‎ ‎， ……2分 ‎ 所以， ………4分 因为在中， ， ‎ 所以， ‎ 则． ……………6分 ‎（2）由（1）得， ， ， ……………8分 ‎ 在中， ， ‎ 代入条件得，解得或6， ………10分 当时， ；当时， ． ………12分 ‎11、解：（Ⅰ）由得-------------------------------2分 ‎，‎ 即，----------------------------------------------4分 ‎∵ ∴；----------------------------------------------------6分 ‎（Ⅱ）在中，因C最大，故最长边为 由，得，-----------------------------------8分 ‎ 由余弦定理得，‎ ‎∴，--------------------------------------------10分 把代入上式得，解得，‎ 即△ABC最长边的长为7．------------------------------------------------------------12分