数学文·广东省韶关市六校联考2017届高三上学期期中数学试卷（文科） Word版含解析]

数学文·广东省韶关市六校联考2017届高三上学期期中数学试卷（文科） Word版含解析]

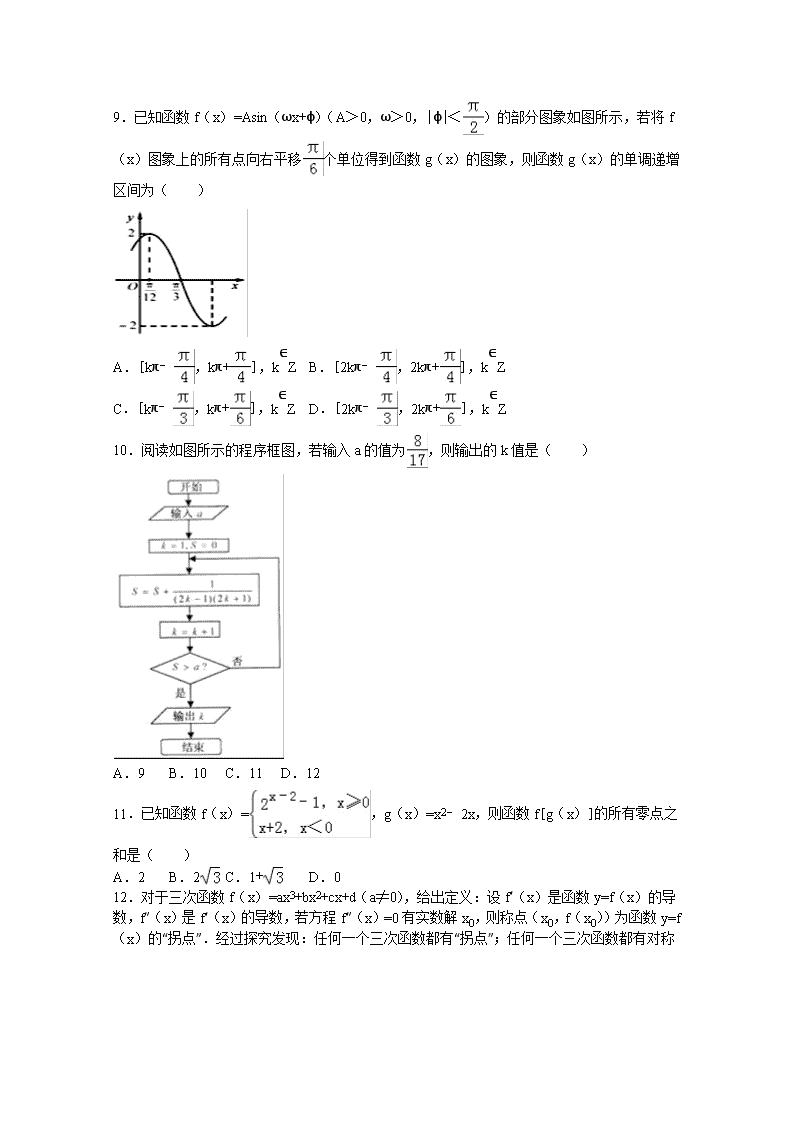
全*品*高*考*网， 用后离不了！2016-2017学年广东省韶关市六校联考高三（上）期中数学试卷（文科）‎ ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分．）‎ ‎1．已知集合M={x|≤0}，N={﹣3，﹣1，1，3，5}，则M∩N=（　　）‎ A．{1，3} B．{﹣1，1，3} C．{﹣3，1} D．{﹣3，﹣1，1}‎ ‎2．已知复数z满足（5+12i）z=169，则=（　　）‎ A．﹣5﹣12i B．﹣5+12i C．5﹣12i D．5+12i ‎3．“cosα=0”是“sinα=1”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎4．已知向量=（﹣1，0），=（，），则向量与的夹角为（　　）‎ A． B． C． D．‎ ‎5．设函数f（x）=﹣x2+4x﹣3，若从区间[2，6]上任取﹣个实数x0，则所选取的实数x0．满足f（x0）≥0的概率为（　　）‎ A． B． C． D．‎ ‎6．椭圆C的焦点在x轴上，一个顶点是抛物线E：y2=16x的焦点，过焦点且垂直于长轴的弦长为2，则椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎7．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形，俯视图是圆心角为的扇形，则该几何体的侧面积为（　　）‎ A．2 B．4+π C．4+π D．4+π+π ‎8．已知α∈（，π），且cosα=﹣，则=（　　）‎ A． B．﹣ C． D．﹣‎ ‎9．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的部分图象如图所示，若将f（x）图象上的所有点向右平移个单位得到函数g（x）的图象，则函数g（x）的单调递增区间为（　　）‎ A．[kπ﹣，kπ+]，k∈Z B．[2kπ﹣，2kπ+]，k∈Z C．[kπ﹣，kπ+]，k∈Z D．[2kπ﹣，2kπ+]，k∈Z ‎10．阅读如图所示的程序框图，若输入a的值为，则输出的k值是（　　）‎ A．9 B．10 C．11 D．12‎ ‎11．已知函数f（x）=，g（x）=x2﹣2x，则函数f[g（x）]的所有零点之和是（　　）‎ A．2 B．2 C．1+ D．0‎ ‎12．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″（x）是f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对 称中心，且“拐点”就是对称中心．设函数g（x）=2x3﹣3x2+，则g（）+g（）+…+g（）=（　　）‎ A．100 B．50 C． D．0‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．已知实数x，y满足，则z=x+2y的最小值为　　．‎ ‎14．已知函数f（x）=lnx﹣ax2，且函数f（x）在点（2，f（2））处的切线的斜率是﹣，则a=　　．‎ ‎15．已知H是球O的直径AB上一点，AH：HB=1：3，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的半径为　　．‎ ‎16．已知△ABC满足BC•AC=2，若C=， =，则AB=　　．‎ ‎　‎ 三、解答题（本大题共70分.解答要有文字说明或推理过程）‎ ‎17．已知等差数列{an}的前n项和为Sn，且S3=9，a1，a3，a7成等比数列．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若an≠a1时，数列{bn}满足bn=2，求数列{bn}的前n项和Tn．‎ ‎18．某商店计划每天购进某商品若干件，商店每销售1件该商品可获利50元．若供大于求，剩余商品全部退回，则每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利30元．‎ ‎（Ⅰ）若商店一天购进该商品10件，求当天的利润y（单位：元）关于当天需求量n（单位：件，n∈N）的函数解析式；‎ ‎（Ⅱ）商店记录了50天该商品的日需求量（单位：件），整理得表：‎ 日需求量n ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 频数 ‎10‎ ‎10‎ ‎15‎ ‎10‎ ‎5‎ ‎①假设该店在这50天内每天购进10件该商品，求这50天的日利润（单位：元）的平均数；‎ ‎②若该店一天购进10件该商品，记“当天的利润在区间[400，550]”为事件A，求P（A）的估计值．‎ ‎19．如图，ABC﹣A1B1C1是底面边长为2，高为的正三棱柱，经过AB的截面与上底面相交于PQ，设C1P=λC1A1（0＜λ＜1）．‎ ‎（Ⅰ）证明：PQ∥A1B1；‎ ‎（Ⅱ）当时，求点C到平面APQB的距离．‎ ‎20．已知椭圆C的两个焦点分别为F1（﹣，0），F2（，0），且椭圆C过点P（3，2）．‎ ‎（Ⅰ）求椭圆C的标准方程；‎ ‎（Ⅱ）与直线OP平行的直线交椭圆C于A，B两点，求△PAB面积的最大值．‎ ‎21．已知函数f（x）=2lnx﹣ax+a（a∈R）．‎ ‎（Ⅰ）讨论f（x）的单调性；‎ ‎（Ⅱ）若f（x）≤0恒成立，证明：当0＜x1＜x2时，．‎ ‎　‎ 请考生在第22、23、24题中任选一题做答。如果多做，则按所做的第一题计分，答题时请写清题号。[选修4—1：几何证明选讲]‎ ‎22．如图，已知圆O是△ABC的外接圆，AB=BC，AD是 BC边上的高，AE 是圆O的直径，过点C作圆O的切线交BA的延长线于点F．‎ ‎（Ⅰ）求证：AC•BC=AD•AE； ‎ ‎（Ⅱ）若AF=2，CF=2，求AE的长．‎ ‎　‎ ‎[选修4—4：坐标系与参数方程]‎ ‎23．在平面直角坐标系xOy中，直线l的参数方程为（ t为参数）．以原点为极点，x轴正半轴为极轴 建立极坐标系，圆C的方程为 ρ=2sinθ．‎ ‎（Ⅰ）写出直线l的普通方程和圆C的直角坐标方程；‎ ‎（Ⅱ）若点P的直角坐标为（1，0），圆C与直线l交于A，B两点，求|PA|+|PB|的值．‎ ‎　‎ ‎[选修4—5：不等式选讲]‎ ‎24．已知函数f（x）=|x+a|+|x+|（a＞0）‎ ‎（Ⅰ）当a=2时，求不等式f（x）＞3的解集；‎ ‎（Ⅱ）证明：．‎ ‎　‎ ‎2016-2017学年广东省韶关市六校联考高三（上）期中数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分．）‎ ‎1．已知集合M={x|≤0}，N={﹣3，﹣1，1，3，5}，则M∩N=（　　）‎ A．{1，3} B．{﹣1，1，3} C．{﹣3，1} D．{﹣3，﹣1，1}‎ ‎【考点】交集及其运算．‎ ‎【分析】求出集合M，然后利用交集的运算法则化简求解即可．‎ ‎【解答】解：集合M={x|≤0}={x|﹣1＜x≤3}，N={﹣3，﹣1，1，3，5}，‎ 则M∩N={1，3}．‎ 故选：A．‎ ‎　‎ ‎2．已知复数z满足（5+12i）z=169，则=（　　）‎ A．﹣5﹣12i B．﹣5+12i C．5﹣12i D．5+12i ‎【考点】复数代数形式的乘除运算．‎ ‎【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简得答案．‎ ‎【解答】解：由（5+12i）z=169，得=5﹣12i，‎ ‎∴，‎ 故选：D．‎ ‎　‎ ‎3．“cosα=0”是“sinα=1”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】由cosα=0可得α=kπ+（k∈Z），即可判断出结论．‎ ‎【解答】解：cosα=0可得α=kπ+（k∈Z），‎ ‎∴sinα=±1，反之成立，‎ ‎∴“cosα=0”是“sinα=1”的必要不充分条件．‎ 故选：B．‎ ‎　‎ ‎4．已知向量=（﹣1，0），=（，），则向量与的夹角为（　　）‎ A． B． C． D．‎ ‎【考点】平面向量数量积的运算．‎ ‎【分析】由已知求出及，代入数量积求夹角公式得答案．‎ ‎【解答】解：∵=（﹣1，0），=（，），‎ ‎∴，||=1，||=1，‎ ‎∴cos＜＞=，‎ 则向量与的夹角为．‎ 故选：B．‎ ‎　‎ ‎5．设函数f（x）=﹣x2+4x﹣3，若从区间[2，6]上任取﹣个实数x0，则所选取的实数x0．满足f（x0）≥0的概率为（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】由题意知本题是一个几何概型，概率的值为对应长度之比，根据题目中所给的不等式解出解集，解集在数轴上对应的线段的长度之比等于要求的概率．‎ ‎【解答】解：由题意知本题是一个几何概型，概率的值为对应长度之比，‎ 由f（x0）≥0，得到﹣x2+4x﹣3≥0，且x0∈[2，6]‎ 解得：2≤x≤3，‎ ‎∴P==，‎ 故选：B．‎ ‎　‎ ‎6．椭圆C的焦点在x轴上，一个顶点是抛物线E：y2=16x的焦点，过焦点且垂直于长轴的弦长为2，则椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】由题意可设椭圆的标准方程为： +=1（a＞b＞0），由抛物线E：y2=16x，可得焦点F（4，0），可得a．又2×=2，a2=b2+c2，联立解出即可得出．‎ ‎【解答】解：由题意可设椭圆的标准方程为： +=1（a＞b＞0），‎ 由抛物线E：y2=16x，可得焦点F（4，0），则a=4．‎ 又2×=2，a2=b2+c2，‎ 联立解得：b=2，c=．‎ ‎∴e==．‎ 故选：D．‎ ‎　‎ ‎7．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形，俯视图是圆心角为的扇形，则该几何体的侧面积为（　　）‎ A．2 B．4+π C．4+π D．4+π+π ‎【考点】棱柱、棱锥、棱台的体积；由三视图求面积、体积．‎ ‎【分析】由已知可得该几何体为以俯视图为底面的锥体，其侧面积由两个腰长为2的两个全等的等腰直角三角形，和一个高为2，底面半径为2的圆锥的四分之一侧面积组成，计算可得答案．‎ ‎【解答】解：由已知可得该几何体为以俯视图为底面的锥体，‎ 其侧面积由两个腰长为2的两个全等的等腰直角三角形，‎ 和一个高为2，底面半径为2的圆锥的四分之一侧面积组成，‎ 故S=2××2×2+×π×2×=4+π，‎ 故选：C．‎ ‎　‎ ‎8．已知α∈（，π），且cosα=﹣，则=（　　）‎ A． B．﹣ C． D．﹣‎ ‎【考点】三角函数的化简求值．‎ ‎【分析】利用诱导公式化简所求的表达式，代入已知条件求解即可．‎ ‎【解答】解：已知α∈（，π），且cosα=﹣，‎ 可得sinα=则===．‎ 故选：C．‎ ‎　‎ ‎9．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的部分图象如图所示，若将f（x）图象上的所有点向右平移个单位得到函数g（x）的图象，则函数g（x）的单调递增区间为（　　）‎ A．[kπ﹣，kπ+]，k∈Z B．[2kπ﹣，2kπ+]，k∈Z C．[kπ﹣，kπ+]，k∈Z D．[2kπ﹣，2kπ+]，k∈Z ‎【考点】函数y=Asin（ωx+φ）的图象变换．‎ ‎【分析】利用y=Asin（ωx+φ）的图象特征，求出函数y=Asin（ωx+φ）的解析式，再根据y=Asin（ωx+φ）的图象变换规律及正弦函数的图象和性质，即可求得函数g（x）的单调增区间．‎ ‎【解答】解：由图可知A=2，T=4（﹣）=π，‎ ‎∴ϖ==2．‎ ‎∵由图可得点（，2）在函数图象上，可得：2sin（2×+φ）=2，解得：2×+φ=2kπ+，k∈Z，‎ ‎∴由|φ|＜，可得：φ=，‎ ‎∴f（x）=2sin（2x+）．‎ ‎∵若将y=f（x）的图象向右平移个单位后，得到的函数解析式为：g（x）=2sin[2（x﹣）+]=2sin2x．‎ ‎∴由2kπ﹣≤2x≤2kπ+，k∈Z，可得kπ﹣≤x≤kπ+，k∈Z，‎ ‎∴函数g（x）的单调增区间为：[kπ﹣，kπ+]，k∈Z．‎ 故选：A．‎ ‎　‎ ‎10．阅读如图所示的程序框图，若输入a的值为，则输出的k值是（　　）‎ A．9 B．10 C．11 D．12‎ ‎【考点】程序框图．‎ ‎【分析】根据程序框图的流程，计算运行n次的结果，根据输入a=，判断n满足的条件，从而求出输出的k值．‎ ‎【解答】解：由程序框图知第一次运行s=0+，k=2；‎ 第二次运行s=0++，k=3；‎ ‎…‎ ‎∴第n次运行s=0+++…+=×（1﹣++…+）=×（1﹣）=，‎ 当输入a=时，由n＞a得n＞8，程序运行了9次，输出的k值为10．‎ 故选：B．‎ ‎　‎ ‎11．已知函数f（x）=，g（x）=x2﹣2x，则函数f[g（x）]的所有零点之和是（　　）‎ A．2 B．2 C．1+ D．0‎ ‎【考点】二分法的定义．‎ ‎【分析】利用函数的解析式，化简函数f[g（x）]的表达式，求出函数的零点，即可求解．‎ ‎【解答】解：g（x）=x2﹣2x=（x﹣1）2﹣1，‎ 当g（x）≥0时，即x（x﹣2）≥0，解得x≤0或x≥2，‎ 当g（x）＜0时，即x（x﹣2）＜0，解得0＜x＜2，‎ ‎∴当x≤0或x≥2，f[g（x）]= =0，即x2﹣2x﹣2=2，解得x=0或x=2，‎ 当0＜x＜2，f[g（x）]=x2﹣2x+2=0，此时方程无解，‎ ‎∴函数f[g（x）]的所有零点之和是0+2=2，‎ 故选：A ‎　‎ ‎12．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″（x）是f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数g（x）=2x3﹣3x2+，则g（）+g（）+…+g（）=（　　）‎ A．100 B．50 C． D．0‎ ‎【考点】函数的值．‎ ‎【分析】由题意对已知函数求两次导数可得图象关于点（，0）对称，即f（x）+f（1﹣x）=0，由此可得到结论．‎ ‎【解答】解：∵g（x）=2x3﹣3x2+，‎ ‎∴g′（x）=6x2﹣6x，g'（x）=12x﹣6，‎ 由g'（x）=0，得x=，‎ 又f（）=2×=0，‎ ‎∴故函数g（x）关于点（，0）对称，‎ ‎∴g（x）+g（1﹣x）=0，‎ ‎∴g（）+g（）+…+g（）=49×=f（）=0．‎ 故选：D．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．已知实数x，y满足，则z=x+2y的最小值为　﹣5　．‎ ‎【考点】简单线性规划．‎ ‎【分析】作出不等式组对应的平面区域，利用z的几何意义即可得到结论．‎ ‎【解答】解：作出不等式组对应的平面区域，‎ 由z=x+2y，得y=，平移直线y=，由图象可知当直线经过点B时，‎ 直线y=的截距最小，此时z最小，‎ 由，得，即B（﹣1，﹣2）‎ 此时z=﹣1+2×（﹣2）=﹣5．‎ 故答案为：﹣5．‎ ‎　‎ ‎14．已知函数f（x）=lnx﹣ax2，且函数f（x）在点（2，f（2））处的切线的斜率是﹣，则a=　　．‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】求出函数f（x）的导数，代入x=2可得切线的斜率，解方程可得a的值．‎ ‎【解答】解：函数f（x）=lnx﹣ax2的导数为f′（x）=﹣2ax，‎ 函数f（x）在点（2，f（2））处的切线的斜率为﹣4a，‎ 由题意可得﹣4a=﹣，‎ 解得a=．‎ 故答案为：．‎ ‎　‎ ‎15．已知H是球O的直径AB上一点，AH：HB=1：3，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的半径为　　．‎ ‎【考点】球的体积和表面积．‎ ‎【分析】设球的半径为R，根据题意知由与球心距离为R的平面截球所得的截面圆的面积是π，我们易求出截面圆的半径为1，根据球心距、截面圆半径、球半径构成直角三角形，满足勾股定理，我们易求出该球的半径．‎ ‎【解答】解：设球的半径为R，∵AH：HB=1：3，∴平面α与球心的距离为R，‎ ‎∵α截球O所得截面的面积为π，‎ ‎∴d=R时，r=1，‎ 故由R2=r2+d2得R2=12+（R）2，∴R2=‎ ‎∴R=．‎ 故答案为．‎ ‎　‎ ‎16．已知△ABC满足BC•AC=2，若C=， =，则AB=　　．‎ ‎【考点】正弦定理．‎ ‎【分析】由已知利用正弦定理，特殊角的三角函数值化简可得b=，由BC•AC=2，可解得a，b的值，利用余弦定理即可得解．‎ ‎【解答】解：设三角形的边AB，BC，AC所对的边分别为c，a，b，‎ ‎∵=，C=，‎ ‎∴=﹣，解得：cosC=﹣=﹣，‎ ‎∴b=，‎ ‎∵BC•AC=2，可得：ab=2，解得：a=，b=2．‎ ‎∴c2=a2+b2﹣2abcosC=5a2=10，‎ ‎∴c=．即AB的值为．‎ 故答案为：．‎ ‎　‎ 三、解答题（本大题共70分.解答要有文字说明或推理过程）‎ ‎17．已知等差数列{an}的前n项和为Sn，且S3=9，a1，a3，a7成等比数列．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若an≠a1时，数列{bn}满足bn=2，求数列{bn}的前n项和Tn．‎ ‎【考点】数列的求和；等比数列的通项公式．‎ ‎【分析】（1）由等差数列前n项和公式、通项公式及等比数列性质，列出方程组，求出首项与公差，由此能求出数列{an}的通项公式．‎ ‎（2）由an≠a1，各bn=2=2n+1，由此能求出数列{bn}的前n项和Tn．‎ ‎【解答】解：（1）∵等差数列{an}的前n项和为Sn，且S3=9，a1，a3，a7成等比数列，‎ ‎∴，解得或，‎ 当时，an=3；‎ 当时，an=2+（n﹣1）=n+1．‎ ‎（2）∵an≠a1，∴an=n+1，∴bn=2=2n+1，‎ ‎∴， =2，‎ ‎∴{bn}是以4为首项，以2为公比的等比数列，‎ ‎∴Tn===2n+2﹣4．‎ ‎　‎ ‎18．某商店计划每天购进某商品若干件，商店每销售1件该商品可获利50元．若供大于求，剩余商品全部退回，则每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利30元．‎ ‎（Ⅰ）若商店一天购进该商品10件，求当天的利润y（单位：元）关于当天需求量n（单位：件，n∈N）的函数解析式；‎ ‎（Ⅱ）商店记录了50天该商品的日需求量（单位：件），整理得表：‎ 日需求量n ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 频数 ‎10‎ ‎10‎ ‎15‎ ‎10‎ ‎5‎ ‎①假设该店在这50天内每天购进10件该商品，求这50天的日利润（单位：元）的平均数；‎ ‎②若该店一天购进10件该商品，记“当天的利润在区间[400，550]”为事件A，求P（A）的估计值．‎ ‎【考点】函数模型的选择与应用．‎ ‎【分析】（Ⅰ）根据题意分段求解得出当1≤n≤10时，y利润，当n＞10时，y利润，‎ ‎（Ⅱ）①50天内有9天获得的利润380元，有11天获得的利润为440元，有15天获得利润为500元，有10天获得的利润为530元，有5天获得的利润为560，求其平均数即可．‎ ‎②当天的利润在区间[400，500]有11+15+10天，即可求解概率．‎ ‎【解答】解：（Ⅰ）当日需求量n≥10时，利润为y=50×10+（n﹣10）×30=30n+200；‎ 当需求量n＜10时，利润y=50×n﹣（10﹣n）×10=60n﹣100．…4‎ 所以利润y与日需求量n的函数关系式为：y=…5‎ ‎（Ⅱ）50天内有10天获得的利润380元，有10天获得的利润为440元，有15天获得利润为500元，有10天获得的利润为530元，有5天获得的利润为560元…8‎ ‎①=476…10‎ ‎②事件A发生当且仅当日需求量n为9或10或11时．由所给数据知，n=9或10或11的频率为f==0.7．‎ 故P（A）的估计值为0.7…12‎ ‎　‎ ‎19．如图，ABC﹣A1B1C1是底面边长为2，高为的正三棱柱，经过AB的截面与上底面相交于PQ，设C1P=λC1A1（0＜λ＜1）．‎ ‎（Ⅰ）证明：PQ∥A1B1；‎ ‎（Ⅱ）当时，求点C到平面APQB的距离．‎ ‎【考点】点、线、面间的距离计算；棱柱的结构特征．‎ ‎【分析】（I）由平面ABC∥平面A1B1C1，利用线面平行的性质定理可得：AB∥PQ，又AB∥A1B1，即可证明PQ∥A1B1．‎ ‎（II）建立如图所示的直角坐标系．设平面APQB的法向量为=（x，y，z），则，利用点C到平面APQB的距离d=即可得出．‎ ‎【解答】证明：（I）∵平面ABC∥平面A1B1C1，平面ABC∩平面ABQP=AB，平面ABQP∩平面A1B1C1=QP，‎ ‎∴AB∥PQ，‎ 又∵AB∥A1B1，‎ ‎∴PQ∥A1B1．‎ 解：（II）建立如图所示的直角坐标系．‎ ‎∴O（0，0，0），P（0，0，），A（0，1，0），B（﹣，0，0），C（0，﹣1，0），‎ ‎∴=（0，﹣1，），=（﹣，﹣1，0），=（0，﹣2，0），‎ 设平面APQB的法向量为=（x，y，z），‎ 则，可得，‎ 取=，‎ ‎∴点C到平面APQB的距离d===．‎ ‎　‎ ‎20．已知椭圆C的两个焦点分别为F1（﹣，0），F2（，0），且椭圆C过点P（3，2）．‎ ‎（Ⅰ）求椭圆C的标准方程；‎ ‎（Ⅱ）与直线OP平行的直线交椭圆C于A，B两点，求△PAB面积的最大值．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（Ⅰ）由题意设椭圆方程为+=1，利用椭圆定义求得a，结合隐含条件求得b，则椭圆方程可求；‎ ‎（Ⅱ）求出kOP=，设与直线OP平行的直线方程为y=x+m，联立直线和椭圆方程，运用韦达定理和判别式大于0，以及弦长公式，点到直线的距离公式和三角形的面积公式，结合基本不等式即可得到所求最大值．‎ ‎【解答】解：（Ⅰ）由题意设椭圆方程为+=1，‎ ‎∵椭圆C的两个焦点分别为F1（﹣，0），‎ F2（，0），且椭圆C过点P（3，2），‎ 由椭圆定义可得2a=+=6，即a=3，‎ ‎∴b2=a2﹣c2=8，‎ 则椭圆C的标准方程为+=1；‎ ‎（Ⅱ）由kOP=，‎ 设与直线OP平行的直线方程为y=x+m，‎ 联立，得8x2+12mx+9m2﹣72=0．‎ 由判别式△=144m2﹣32（9m2﹣72）＞0，解得0＜|m|＜4．‎ 设A（x1，y1），B（x2，y2），则x1+x2=﹣m，x1x2=，‎ ‎|AB|=•=•，‎ 点O到直线AB的距离为d==|m|，‎ 即有△PAB面积为S=|AB|d==≤=6．‎ 当且仅当9m2=144﹣9m2，即m=±2时，取得最大值6．‎ ‎　‎ ‎21．已知函数f（x）=2lnx﹣ax+a（a∈R）．‎ ‎（Ⅰ）讨论f（x）的单调性；‎ ‎（Ⅱ）若f（x）≤0恒成立，证明：当0＜x1＜x2时，．‎ ‎【考点】利用导数研究函数的单调性；函数单调性的性质．‎ ‎【分析】（I）利用导数的运算法则可得f′（x），对a分类讨论即可得出其单调性；‎ ‎（II）通过对a分类讨论，得到当a=2，满足条件且lnx≤x﹣1（当且仅当x=1时取“=”）．利用此结论即可证明．‎ ‎【解答】解：（Ⅰ）求导得f′（x）=，x＞0．‎ 若a≤0，f′（x）＞0，f（x）在（0，+∞）上递增；‎ 若a＞0，当x∈（0，）时，f′（x）＞0，f（x）单调递增；‎ 当x∈（，+∞）时，f′（x）＜0，f（x）单调递减．‎ ‎（Ⅱ）由（Ⅰ）知，若a≤0，f（x）在（0，+∞）上递增，‎ 又f（1）=0，故f（x）≤0不恒成立．‎ 若a＞2，当x∈（，1）时，f（x）递减，f（x）＞f（1）=0，不合题意．‎ 若0＜a＜2，当x∈（1，）时，f（x）递增，f（x）＞f（1）=0，不合题意．‎ 若a=2，f（x）在（0，1）上递增，在（1，+∞）上递减，‎ f（x）≤f（1）=0，合题意．‎ 故a=2，且lnx≤x﹣1（当且仅当x=1时取“=”）．‎ 当0＜x1＜x2时，f（x2）﹣f（x1）=2ln﹣2（x2﹣x1）‎ ‎＜2（﹣1）﹣2（x2﹣x1）‎ ‎=2（﹣1）（x2﹣x1），‎ ‎∴＜2（﹣1）．‎ ‎　‎ 请考生在第22、23、24题中任选一题做答。如果多做，则按所做的第一题计分，答题时请写清题号。[选修4—1：几何证明选讲]‎ ‎22．如图，已知圆O是△ABC的外接圆，AB=BC，AD是 BC边上的高，AE 是圆O的直径，过点C作圆O的切线交BA的延长线于点F．‎ ‎（Ⅰ）求证：AC•BC=AD•AE； ‎ ‎（Ⅱ）若AF=2，CF=2，求AE的长．‎ ‎【考点】与圆有关的比例线段．‎ ‎【分析】（I）如图所示，连接BE．由于AE是⊙O的直径，可得∠ABE=90°．利用∠E与∠ACB都是所对的圆周角，可得∠E=∠ACB．进而得到△ABE∽△ADC，即可得到．‎ ‎（II）利用切割线定理可得CF2=AF•BF，可得BF．再利用△AFC∽△CFB，可得AF：FC=AC：BC，进而根据sin∠ACD=sin∠AEB，即可得出答案．‎ ‎【解答】证明：（I）如图所示，连接BE．‎ ‎∵AE是⊙O的直径，∴∠ABE=90°．‎ 又∠E与∠ACB都是所对的圆周角，‎ ‎∴∠E=∠ACB．‎ ‎∵AD⊥BC，∠ADC=90°．‎ ‎∴△ABE∽△ADC，‎ ‎∴AB：AD=AE：AC，‎ ‎∴AB•AC=AD•AE．‎ 又AB=BC，‎ ‎∴BC•AC=AD•AE．‎ 解：（II）∵CF是⊙O的切线，‎ ‎∴CF2=AF•BF，‎ ‎∵AF=2，CF=2，‎ ‎∴（2）2=2BF，解得BF=4．‎ ‎∴AB=BF﹣AF=2．‎ ‎∵∠ACF=∠FBC，∠CFB=∠AFC，‎ ‎∴△AFC∽△CFB，‎ ‎∴AF：FC=AC：BC，‎ ‎∴AC==．‎ ‎∴cos∠ACD=，‎ ‎∴sin∠ACD==sin∠AEB，‎ ‎∴AE=．‎ ‎　‎ ‎[选修4—4：坐标系与参数方程]‎ ‎23．在平面直角坐标系xOy中，直线l的参数方程为（ t为参数）．以原点为极点，x轴正半轴为极轴 建立极坐标系，圆C的方程为 ρ=2sinθ．‎ ‎（Ⅰ）写出直线l的普通方程和圆C的直角坐标方程；‎ ‎（Ⅱ）若点P的直角坐标为（1，0），圆C与直线l交于A，B两点，求|PA|+|PB|的值．‎ ‎【考点】直线的参数方程．‎ ‎【分析】（Ⅰ）直线l的参数方程为（ t为参数）．消去参数得直线普通方程，由圆C的方程为 ρ=2sinθ，即ρ2=2ρsinθ，利用互化公式可得圆C的直角坐标方程．‎ ‎（Ⅱ）把直线l的参数方程代入圆C的直角坐标方程，得t2﹣4t+1=0，△＞0．利用|PA|+|PB|=|t1|+|t2|=|t1+t2|．即可得出．‎ ‎【解答】解：（Ⅰ）直线l的参数方程为（ t为参数）．‎ 消去参数得直线普通方程为x+y﹣=0，‎ 由圆C的方程为 ρ=2sinθ，即ρ2=2ρsinθ，‎ 可得圆C的直角坐标方程：x2+y2=2y．‎ ‎（Ⅱ）直线l的参数方程为（ t为参数）．‎ 把直线l的参数方程代入圆C的直角坐标方程，得t2﹣4t+1=0，△＞0．‎ ‎∴t1+t2=4，t1t2=1．‎ ‎∴|PA|+|PB|=|t1|+|t2|=|t1+t2|=4．‎ ‎　‎ ‎[选修4—5：不等式选讲]‎ ‎24．已知函数f（x）=|x+a|+|x+|（a＞0）‎ ‎（Ⅰ）当a=2时，求不等式f（x）＞3的解集；‎ ‎（Ⅱ）证明：．‎ ‎【考点】绝对值三角不等式；基本不等式．‎ ‎【分析】（Ⅰ）当a=2时，求不等式即|x+2|+|x+|＞3，再利用对值的意义求得它的解集．‎ ‎（Ⅱ）由条件利用绝对值三角不等式、基本不等式，证得要证的结论．‎ ‎【解答】解：（Ⅰ）当a=2时，求不等式f（x）＞3，即|x+2|+|x+|＞3．‎ 而|x+2|+|x+|表示数轴上的x对应点到﹣2、﹣对应点的距离之和，‎ 而0和﹣3对应点到﹣、对应点的距离之和正好等于3，‎ 故不等式f（x）＞3的解集为{x|x＜﹣，或 x＞}．‎ ‎（Ⅱ）证明：∵f（m）+f（﹣）=|m+a|+|m+|+|﹣+a||﹣+|‎ ‎=（|m+a|+|﹣+a|）+（|m+|+|﹣+|）≥2（|m+|）=2（|m|+||）≥4，‎ ‎∴要证得结论成立．‎ ‎　‎ ‎2016年12月1日