数学文卷·2019届北京市昌平临川育人学校高二上学期期中考试（2017-11）

数学文卷·2019届北京市昌平临川育人学校高二上学期期中考试（2017-11）

北京临川学校2017-2018学年上学期期中考试 高二数学（文科）试卷 密封线内不要答题 学校_____________班级_______________座号________________姓名______________‎ 时间：120分钟 满分：150分 ‎ ‎ 一、选择题（每题5分，共60分）‎ ‎1.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异，拟从这三个年级中按人数比例抽取部分学生进行调查，则最合理的抽样方法是( )‎ A．抽签法 B．系统抽样法 ( C．分层抽样法 D．随机数法 ‎2.重庆市2013年各月的平均气温（°C）数据的茎叶图如下 ‎0‎ ‎8‎ ‎9‎ ‎1‎ ‎2‎ ‎5‎ ‎8‎ ‎2‎ ‎0‎ ‎0‎ ‎3‎ ‎3‎ ‎8‎ ‎3‎ ‎1 ‎ ‎2‎ 则这组数据中的极差是（ ）‎ A．19 B．20 C． 21.5 D．23‎ ‎3．某入伍新兵的打靶练习中，连续射击2次，则事件“至少有1次中靶”的互斥事件是(　　)‎ A．至多有1次中靶 B．2次都中靶 C．2次都不中靶 D．只有1次中靶 ‎4. 在区间[－1,2]上随机取一个数x，则|x|≤1的概率为 A． B． C． D． ‎5. 为评估一种农作物的种植效果，选了n块地作试验田．这n块地的亩产量（单位：‎ kg）分别为x1，x2，…，xn，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 A．x1，x2，…，xn的平均数 B．x1，x2，…，xn的标准差 C．x1，x2，…，xn的最大值 D．x1，x2，…，xn的中位数 ‎6.执行如图所示的程序框图，输出的值为 ‎（A）2 （B）‎ ‎（C） （D）‎ ‎7.“－20）的一条渐近线方程为，则a= .‎ ‎14.如图，在边长为1的正方形中，随机撒1000粒豆子，有180粒落到阴影部分，据此估计阴影部分的面积为___________.‎ ‎15.假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料： （☆P22 8）‎ x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.2‎ ‎3.8‎ ‎5.5‎ ‎6.5‎ ‎7.0‎ 由资料可知y对x呈 （正，负，不）相关。‎ ‎16. 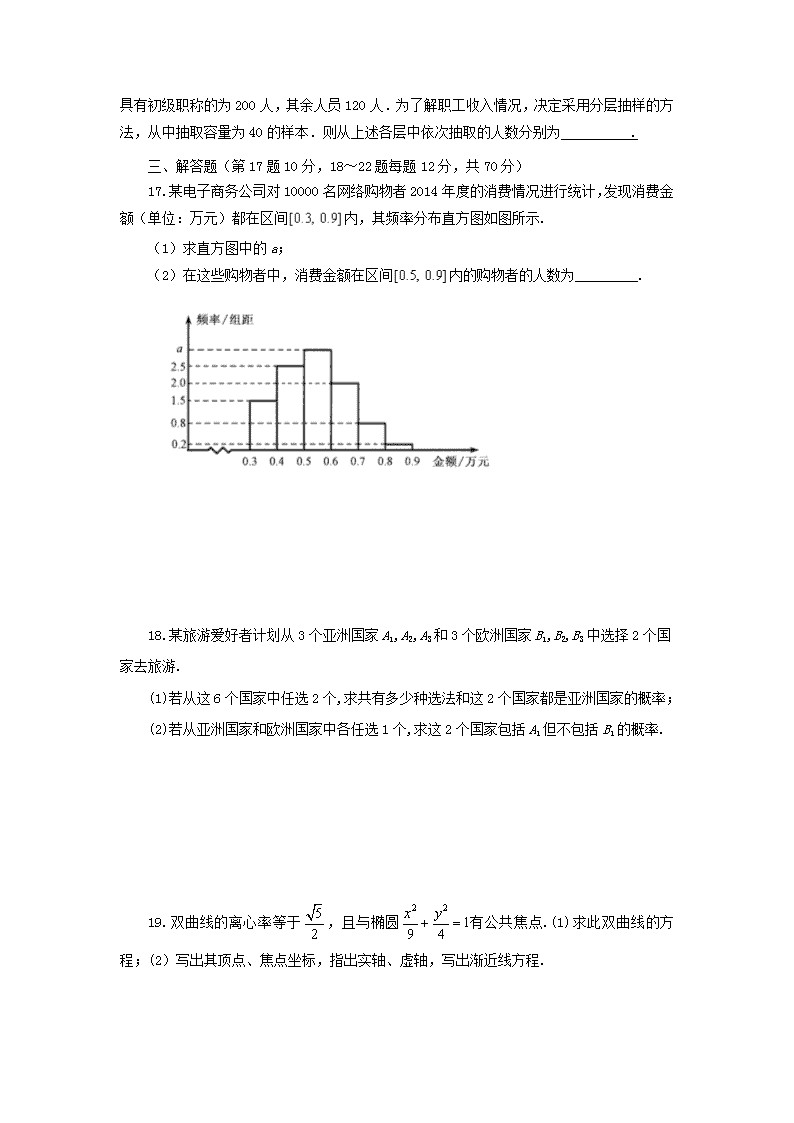‎ 一个单位有职工800人，其中具有高级职称的为160人，具有中级职称的为320人，具有初级职称的为200人，其余人员120人．为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本．则从上述各层中依次抽取的人数分别为 .‎ 三、解答题（第17题10分，18～22题每题12分，共70分）‎ ‎17.某电子商务公司对10000名网络购物者2014年度的消费情况进行统计，发现消费金额（单位：万元）都在区间内，其频率分布直方图如图所示. ‎ ‎（1）求直方图中的a；‎ ‎（2）在这些购物者中，消费金额在区间内的购物者的人数为_________. ‎ ‎ ‎ ‎18.某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.‎ ‎(1)若从这6个国家中任选2个,求共有多少种选法和这2个国家都是亚洲国家的概率；‎ ‎(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.‎ ‎ 19.双曲线的离心率等于，且与椭圆有公共焦点.(1)求此双曲线的方程；(2）写出其顶点、焦点坐标，指出实轴、虚轴，写出渐近线方程. ‎ ‎20.已知斜率为1的直线l过椭圆＋y2＝1的右焦点F交椭圆于A、B两点，求弦AB的长．‎ ‎21.已知直线l经过抛物线y2＝4x的焦点F，与抛物线相交于A,B两点．‎ ‎（1）若|AF|＝4，求点A的坐标和△AOF的面积为 ‎ ‎（2）若|AF|＝4，求弦AB的中点到准线的距离.‎ ‎22.已知椭圆C：的一个顶点为A(2,0)，离心率为.直线y＝k(x－1)与椭圆C交于不同的两点M，N.‎ ‎（1）求椭圆C的方程；‎ ‎（2）当△AMN的面积为时，求k的值．‎ 北京临川学校2017-2018学年上学期期中考试 高二数学（文科）试卷参考答案 时间：120分钟 满分：150分 ‎ ‎ 一、选择题（每题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C B C D B C A B A A C B 二、填空题（每题5分，共20分）‎ ‎13.4‎ ‎14.‎ ‎15.正 ‎16.8,16,10,6‎ 三、解答题（第17题10分，18～22题每题12分，共70分）‎ ‎17.（1）3；（2）6000.‎ ‎【解析】由频率分布直方图及频率和等于1可得，‎ 解之得.于是消费金额在区间内频率为，所以消费金额在区间内的购物者的人数为：，故应填3；6000.‎ ‎18.‎ 所选两个国家都是亚洲的事件所包含的基本事件有：‎ ‎,共个，所以所求事件的概率为；‎ ‎（2）从亚洲国家和欧洲国家中各任选一个，其一切可能的结果组成的基本事件有：‎ 共个，‎ 包含但不包括的事件所包含的基本事件有共个，‎ 所以所求事件的概率为.‎ ‎19.解：(1) (2)顶点（-2,0） （2,0） 焦点 实轴4 虚轴2 ‎ 渐近线方程 ‎20.解　设A、B的坐标分别为A(x1，y1)、B(x2，y2)．‎ 由椭圆的方程知a2＝4，b2＝1，c2＝3，∴F(，0)．‎ 直线l的方程为y＝x－.①‎ 将①代入＋y2＝1，化简整理得5x2－8x＋8＝0，‎ ‎∴x1＋x2＝，x1x2＝，‎ ‎∴|AB|＝＝＝.‎ ‎21.解（1）S△POF＝.（2）‎ ‎22.解：(1)由题意得解得b＝，所以椭圆C的方程为＋＝1.‎ ‎(2)由得(1＋2k2)x2－4k2x＋2k2－4＝0.‎ 设点M，N的坐标分别为(x1，y1)，(x2，y2)，则y1＝k(x1－1)，y2＝k(x2－1)，x1＋x2＝，‎ x1x2＝，所以|MN|＝＝ ‎＝.又因为点A(2,0)到直线y＝k(x－1)的距离d＝，‎ 所以△AMN的面积为S＝|MN|· d＝.‎ 由＝，化简得7k4－2k2－5＝0，解得k＝±1.‎