数学卷·2018届陕西省汉中市南郑中学高二上学期期中数学试卷（解析版）

数学卷·2018届陕西省汉中市南郑中学高二上学期期中数学试卷（解析版）

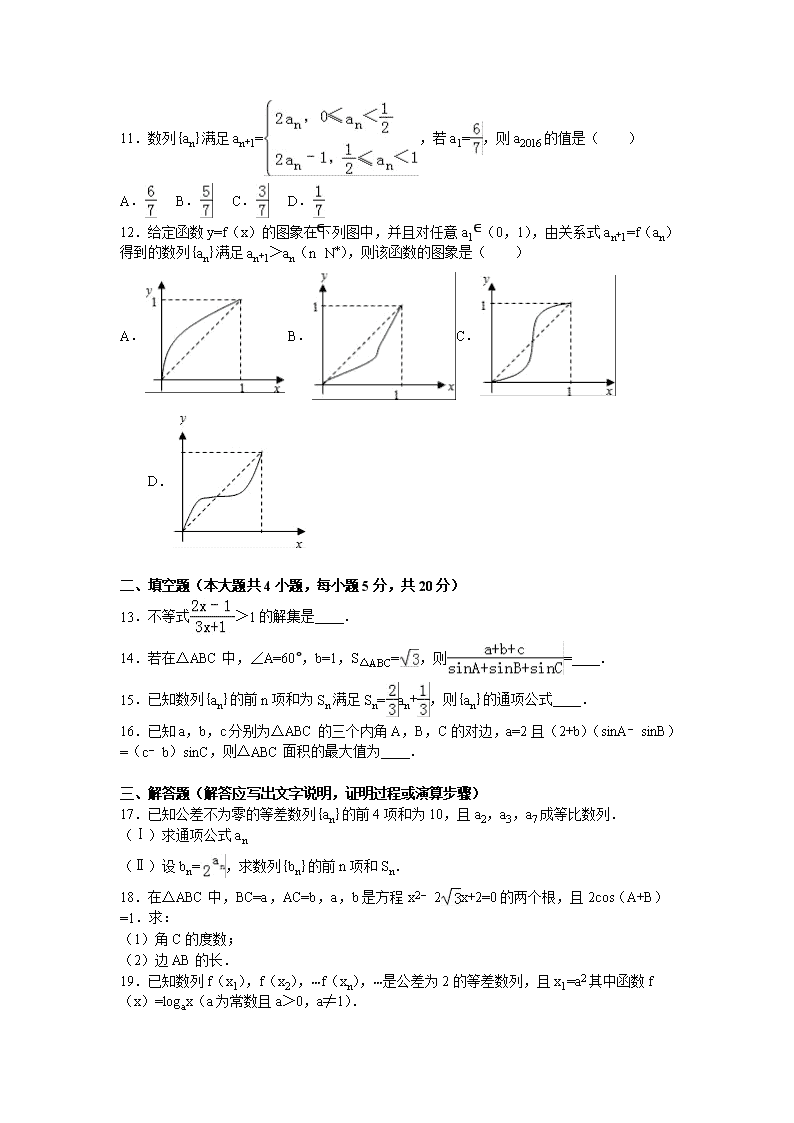
‎2016-2017学年陕西省汉中市南郑中学高二（上）期中数学试卷 ‎　‎ 一、选择题：每小题只有1个正确答案，请把正确答案涂在答题卷（卡）相应位置．‎ ‎1．已知x＞0，函数y=+x的最小值是（　　）‎ A．5 B．4 C．8 D．6‎ ‎2．△ABC中，若a=1，c=2，B=60°，则△ABC的面积为（　　）‎ A． B． C．1 D．‎ ‎3．古代中国数学辉煌灿烂，在《张丘建算经》中记载：“今有十等人，大官甲等十人官赐金，以等次差降之．上三人先入，得金四斤持出；下四人后入，得金三斤持出；中央三人未到者，亦依等次更给．问：各得金几何及未到三人复应得金几何？”则该问题中未到三人共得金多少斤？（　　）‎ A． B． C．2 D．‎ ‎4．不等式ax2+bx+c＜0（a≠0）的解集为R，那么（　　）‎ A．a＜0，△＜0 B．a＜0，△≤0 C．a＞0，△≥0 D．a＞0，△＞0‎ ‎5．设x，y满足约束条件，则z=3x+y的最大值为（　　）‎ A．5 B．3 C．7 D．﹣8‎ ‎6．在△ABC中，a=80，b=100，A=45°，则此三角形解的情况是（　　）‎ A．一解 B．两解 C．一解或两解 D．无解 ‎7．对于任意实数a，b，c，d，下列命题中正确的是（　　）‎ A．若a＞b，c≠0，则ac＞bc B．若a＞b，则ac2＞bc2‎ C．若ac2＞bc2，则a＞b D．若a＞b，则 ‎8．在△ABC中，如果sinA：sinB：sinC=2：3：4，那么cosC等于（　　）‎ A． B． C． D．‎ ‎9．设等差数列{an}的前n项和为Sn，若a1=﹣11，a4+a6=﹣6，则当Sn取最小值时，n等于（　　）‎ A．6 B．7 C．8 D．9‎ ‎10．下列说法错误的是（　　）‎ A．如果命题“￢p”与命题“p∨q”都是真命题，那么命题q一定是真命题 B．命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0”‎ C．若命题p：∃x0∈R，x02+2x0﹣3＜0，则¬p：∀x∈R，x2+2x﹣3≥0‎ D．“sinθ=”是“θ=30°”的充分不必要条件 ‎11．数列{an}满足an+1=，若a1=，则a2016的值是（　　）‎ A． B． C． D．‎ ‎12．给定函数y=f（x）的图象在下列图中，并且对任意a1∈（0，1），由关系式an+1=f（an）得到的数列{an}满足an+1＞an（n∈N*），则该函数的图象是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．不等式＞1的解集是　　．‎ ‎14．若在△ABC中，∠A=60°，b=1，S△ABC=，则=　　．‎ ‎15．已知数列{an}的前n项和为Sn满足Sn=an+，则{an}的通项公式　　．‎ ‎16．已知a，b，c分别为△ABC的三个内角A，B，C的对边，a=2且（2+b）（sinA﹣sinB）=（c﹣b）sinC，则△ABC面积的最大值为　　．‎ ‎　‎ 三、解答题（解答应写出文字说明，证明过程或演算步骤）‎ ‎17．已知公差不为零的等差数列{an}的前4项和为10，且a2，a3，a7成等比数列．‎ ‎（Ⅰ）求通项公式an ‎（Ⅱ）设bn=，求数列{bn}的前n项和Sn．‎ ‎18．在△ABC中，BC=a，AC=b，a，b是方程x2﹣2x+2=0的两个根，且2cos（A+B）=1．求：‎ ‎（1）角C的度数；‎ ‎（2）边AB的长．‎ ‎19．已知数列f（x1），f（x2），…f（xn），…是公差为2的等差数列，且x1=a2其中函数f（x）=logax（a为常数且a＞0，a≠1）．‎ ‎（Ⅰ）求数列{xn}的通项公式；‎ ‎（Ⅱ）若an=logaxn，求证++…+＜1．‎ ‎20．根据下列算法语句，将输出的A值依次记为a1，a2，…，an，…，a2015；已知函数f（x）=a2sin（ωx+φ）（ω＞0，|φ|＜）的最小正周期是a1，且函数y=f（x）的图象关于直线x=对称．‎ ‎（Ⅰ）求函数y=f（x）表达式；‎ ‎（Ⅱ）已知△ABC中三边a，b，c对应角A，B，C，a=4，b=4，∠A=30°，求f（B）．‎ ‎21．某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元．该公司第n年需要付出设备的维修和工人工资等费用an的信息如图．‎ ‎（1）求an；‎ ‎（2）引进这种设备后，第几年后该公司开始获利；‎ ‎（3）这种设备使用多少年，该公司的年平均获利最大？‎ ‎22．设等比数列{an}的前n项和为Sn，已知a1=2，且4S1，3S2，2S3成等差数列．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=|2n﹣5|•an，求数列{bn}的前n项和Tn．‎ ‎　‎ ‎2016-2017学年陕西省汉中市南郑中学高二（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、选择题：每小题只有1个正确答案，请把正确答案涂在答题卷（卡）相应位置．‎ ‎1．已知x＞0，函数y=+x的最小值是（　　）‎ A．5 B．4 C．8 D．6‎ ‎【考点】基本不等式．‎ ‎【分析】由于 x＞0，利用基本不等式求得函数的最小值．‎ ‎【解答】解：∵x＞0，函数≥2=4，当且仅当x=，x=2时，等号成立，‎ 故函数的最小值是4，‎ 故选：B．‎ ‎　‎ ‎2．△ABC中，若a=1，c=2，B=60°，则△ABC的面积为（　　）‎ A． B． C．1 D．‎ ‎【考点】三角形的面积公式．‎ ‎【分析】利用三角形面积公式S△ABC=即可得出．‎ ‎【解答】解：S△ABC===．‎ 故选B．‎ ‎　‎ ‎3．古代中国数学辉煌灿烂，在《张丘建算经》中记载：“今有十等人，大官甲等十人官赐金，以等次差降之．上三人先入，得金四斤持出；下四人后入，得金三斤持出；中央三人未到者，亦依等次更给．问：各得金几何及未到三人复应得金几何？”则该问题中未到三人共得金多少斤？（　　）‎ A． B． C．2 D．‎ ‎【考点】等差数列的通项公式．‎ ‎【分析】设第十等人得金a1斤，第九等人得金a2斤，以此类推，第一等人得金a10斤，利用等差数列的通项公式即可得出．‎ ‎【解答】解：设第十等人得金a1斤，第九等人得金a2斤，以此类推，第一等人得金a10斤，‎ 则数列{an}构成等差数列，设公差为d，则每一等人比下一等人多得d斤金，‎ 由题意得，即，‎ 解得d=，a1=．‎ ‎∴该问题中未到三人共得金=a5+a6+a7=3a1+15d=斤．‎ 故选：D．‎ ‎　‎ ‎4．不等式ax2+bx+c＜0（a≠0）的解集为R，那么（　　）‎ A．a＜0，△＜0 B．a＜0，△≤0 C．a＞0，△≥0 D．a＞0，△＞0‎ ‎【考点】二次函数的性质．‎ ‎【分析】由不等式ax2+bx+c＜0（a≠0）的解集为R，知a＜0，且△=b2﹣4ac＜0．‎ ‎【解答】解：∵不等式ax2+bx+c＜0（a≠0）的解集为R，‎ ‎∴a＜0，‎ 且△=b2﹣4ac＜0，‎ 综上，不等式ax2+bx+c＜0（a≠0）的解集为的条件是：a＜0且△＜0．‎ 故选A．‎ ‎　‎ ‎5．设x，y满足约束条件，则z=3x+y的最大值为（　　）‎ A．5 B．3 C．7 D．﹣8‎ ‎【考点】简单线性规划．‎ ‎【分析】首先作出可行域，再作出直线l0：y=﹣3x，将l0平移与可行域有公共点，直线y=﹣3x+z在y轴上的截距最大时，z有最大值，求出此时直线y=﹣3x+z经过的可行域内的点A的坐标，代入z=3x+y中即可．‎ ‎【解答】解：如图，作出可行域，作出直线l0：y=﹣3x，将l0平移至过点A（3，﹣2）处时，函数z=3x+y有最大值7．‎ 故选C．‎ ‎　‎ ‎6．在△ABC中，a=80，b=100，A=45°，则此三角形解的情况是（　　）‎ A．一解 B．两解 C．一解或两解 D．无解 ‎【考点】正弦定理．‎ ‎【分析】由a，b及sinA的值，利用正弦定理即可求出sinB的值，发现B的值有两种情况，即得到此三角形有两解．‎ ‎【解答】解：由正弦定理得： =，‎ 即sinB==，‎ 则B=arcsin或π﹣arcsin，‎ 即此三角形解的情况是两解．‎ 故选B ‎　‎ ‎7．对于任意实数a，b，c，d，下列命题中正确的是（　　）‎ A．若a＞b，c≠0，则ac＞bc B．若a＞b，则ac2＞bc2‎ C．若ac2＞bc2，则a＞b D．若a＞b，则 ‎【考点】不等关系与不等式．‎ ‎【分析】对于A、当c＜0时，不成立；对于B、当c=0时，不成立；D、当a＞0．b＜0时，不成立，从而得出正确选项．‎ ‎【解答】解：A、当c＜0时，不成立；‎ B、当c=0时，不成立 C、∵ac2＞bc2，∴c≠0，∴c2＞0‎ ‎∴一定有a＞b．故C成立；‎ D、当a＞0．b＜0时，不成立；‎ 故选C．‎ ‎　‎ ‎8．在△ABC中，如果sinA：sinB：sinC=2：3：4，那么cosC等于（　　）‎ A． B． C． D．‎ ‎【考点】余弦定理．‎ ‎【分析】由正弦定理可得；sinA：sinB：sinC=a：b：c，可设a=2k，b=3k，c=4k（k＞0），由余弦定理可求得答案．‎ ‎【解答】解：由正弦定理可得；sinA：sinB：sinC=a：b：c=2：3：4‎ 可设a=2k，b=3k，c=4k（k＞0）‎ 由余弦定理可得， =‎ 故选：D ‎　‎ ‎9．设等差数列{an}的前n项和为Sn，若a1=﹣11，a4+a6=﹣6，则当Sn取最小值时，n等于（　　）‎ A．6 B．7 C．8 D．9‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】条件已提供了首项，故用“a1，d”法，再转化为关于n的二次函数解得．‎ ‎【解答】解：设该数列的公差为d，则a4+a6=2a1+8d=2×（﹣11）+8d=﹣6，解得d=2，‎ 所以，所以当n=6时，Sn取最小值．‎ 故选A．‎ ‎　‎ ‎10．下列说法错误的是（　　）‎ A．如果命题“￢p”与命题“p∨q”都是真命题，那么命题q一定是真命题 B．命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0”‎ C．若命题p：∃x0∈R，x02+2x0﹣3＜0，则¬p：∀x∈R，x2+2x﹣3≥0‎ D．“sinθ=”是“θ=30°”的充分不必要条件 ‎【考点】命题的真假判断与应用．‎ ‎【分析】由复合命题的真假和真值表，可判断A；由否命题的形式，既对条件否定，又对结论否定，可判断B；由含有一个量词的命题的否定形式，可判断C；根据充分必要的定义，结合诱导公式，即可判断D．‎ ‎【解答】解：A．如果命题“￢p”与命题“p∨q”都是真命题，则p为假命题，q一定是真命题，故A正确；‎ B．命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0”，故B正确；‎ C．若命题p：∃x0∈R，x02+2x0﹣3＜0，则¬p：∀x∈R，x2+2x﹣3≥0，故C正确；‎ D．θ=30°可推出sinθ=，但sinθ=推不出θ=30°，因为sin150°=，故“sinθ=”是“θ=30°”的必要不充分条件，故D错．‎ 故选D．‎ ‎　‎ ‎11．数列{an}满足an+1=，若a1=，则a2016的值是（　　）‎ A． B． C． D．‎ ‎【考点】数列的概念及简单表示法．‎ ‎【分析】由数列{an}满足an+1=，a1=，可得an+3=an．‎ ‎【解答】解：∵数列{an}满足an+1=，a1=，‎ ‎∴a2=2a1﹣1=，a3=2a2﹣1=，a4=2a3=，…，‎ ‎∴an+3=an．‎ 则a2016=a671×3+3=a3=．‎ 故选：C．‎ ‎　‎ ‎12．给定函数y=f（x）的图象在下列图中，并且对任意a1∈（0，1），由关系式an+1=f（an）得到的数列{an}满足an+1＞an（n∈N*），则该函数的图象是（　　）‎ A． B． C． D．‎ ‎【考点】数列的函数特性；函数的图象；数列递推式．‎ ‎【分析】由关系式an+1=f（an）得到的数列{an}满足an+1＞an（n∈N*），根据点与直线之间的位置关系，我们不难得到，f（x）的图象在y=x上方．逐一分析不难得到正确的答案．‎ ‎【解答】解：由an+1=f（an）＞an知 f（x）的图象在y=x上方．‎ 故选A ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．不等式＞1的解集是　{x|﹣2＜x＜﹣}　．‎ ‎【考点】其他不等式的解法．‎ ‎【分析】把不等式右边的“1”移项到不等式左边，通分后根据分母不变只把分子相减计算后，在不等式两边同时除以﹣1，不等号方向改变，然后根据两数相除，异号得负，根据商为负数得到x+2与3x+1异号，可化为两个不等式组，分别求出两不等式组的解集，求出两解集的并集即可得到原不等式的解集．‎ ‎【解答】解：不等式，‎ 移项得：＞0，‎ 即＜0，‎ 可化为：或，‎ 解得：﹣2＜x＜﹣或无解，‎ 则原不等式的解集是{x|﹣2＜x＜﹣}．‎ 故答案为：{x|﹣2＜x＜﹣}‎ ‎　‎ ‎14．若在△ABC中，∠A=60°，b=1，S△ABC=，则=　　．‎ ‎【考点】正弦定理；同角三角函数基本关系的运用．‎ ‎【分析】又A的度数求出sinA和cosA的值，根据sinA的值，三角形的面积及b的值，利用三角形面积公式求出c的值，再由cosA，b及c的值，利用余弦定理求出a的值，最后根据正弦定理及比例性质即可得到所求式子的比值．‎ ‎【解答】解：由∠A=60°，得到sinA=，cosA=，‎ 又b=1，S△ABC=，‎ ‎∴bcsinA=×1×c×=，‎ 解得c=4，‎ 根据余弦定理得：a2=b2+c2﹣2bccosA=1+16﹣4=13，‎ 解得a=，‎ 根据正弦定理====，‎ 则=．‎ 故答案为：‎ ‎　‎ ‎15．已知数列{an}的前n项和为Sn满足Sn=an+，则{an}的通项公式　　．‎ ‎【考点】数列递推式．‎ ‎【分析】由数列递推式求出数列首项，进一步得到数列{an}是以1为首项，以﹣2为公比的等比数列，再由等比数列的通项公式得答案．‎ ‎【解答】解：由Sn=an+，得，解得a1=1；‎ 当n≥2时，由Sn=an+，得Sn﹣1=an﹣1+，‎ 两式作差可得，‎ 即an=﹣2an﹣1 （n≥2），‎ ‎∴数列{an}是以1为首项，以﹣2为公比的等比数列，‎ 则．‎ 故答案为：．‎ ‎　‎ ‎16．已知a，b，c分别为△ABC的三个内角A，B，C的对边，a=2且（2+b）（sinA﹣sinB）=（c﹣b）sinC，则△ABC面积的最大值为　　．‎ ‎【考点】余弦定理；正弦定理．‎ ‎【分析】由正弦定理化简已知可得2a﹣b2=c2﹣bc，结合余弦定理可求A的值，由基本不等式可求bc≤4，再利用三角形面积公式即可计算得解．‎ ‎【解答】解：因为：（2+b）（sinA﹣sinB）=（c﹣b）sinC ‎⇒（2+b）（a﹣b）=（c﹣b）c ‎⇒2a﹣b2=c2﹣bc，‎ 又因为：a=2，‎ 所以：，‎ ‎△ABC面积，‎ 而b2+c2﹣a2=bc ‎⇒b2+c2﹣bc=a2‎ ‎⇒b2+c2﹣bc=4‎ ‎⇒bc≤4‎ 所以：，即△ABC面积的最大值为．‎ 故答案为：．‎ ‎　‎ 三、解答题（解答应写出文字说明，证明过程或演算步骤）‎ ‎17．已知公差不为零的等差数列{an}的前4项和为10，且a2，a3，a7成等比数列．‎ ‎（Ⅰ）求通项公式an ‎（Ⅱ）设bn=，求数列{bn}的前n项和Sn．‎ ‎【考点】数列的求和；等差数列的通项公式．‎ ‎【分析】（I）由题意可得，，解方程可求a1，d，进而可求通项 ‎（II）由bn==23n﹣5=，结合等比数列的求和公式即可求解 ‎【解答】解：（I）由题意可得，‎ ‎∵d≠0‎ ‎∴‎ ‎∴an=3n﹣5‎ ‎（II）∵bn==23n﹣5=‎ ‎∴数列{bn}是以为首项，以8为公比的等比数列 ‎∴=‎ ‎　‎ ‎18．在△ABC中，BC=a，AC=b，a，b是方程x2﹣2x+2=0的两个根，且2cos（A+B）=1．求：‎ ‎（1）角C的度数；‎ ‎（2）边AB的长．‎ ‎【考点】余弦定理；一元二次方程的根的分布与系数的关系．‎ ‎【分析】（1）根据三角形内角和可知cosC=cos[π﹣（A+B）]进而根据题设条件求得cosC，则C可求．‎ ‎（2）根据韦达定理可知a+b和ab的值，进而利用余弦定理求得AB．‎ ‎【解答】解：（1）‎ ‎∴C=120°‎ ‎（2）由题设：‎ ‎∴AB2=AC2+BC2﹣2AC•BCcosC=a2+b2﹣2abcos120°‎ ‎=‎ ‎∴‎ ‎　‎ ‎19．已知数列f（x1），f（x2），…f（xn），…是公差为2的等差数列，且x1=a2其中函数f（x）=logax（a为常数且a＞0，a≠1）．‎ ‎（Ⅰ）求数列{xn}的通项公式；‎ ‎（Ⅱ）若an=logaxn，求证++…+＜1．‎ ‎【考点】数列与函数的综合．‎ ‎【分析】（Ⅰ）由已知可得f（x1）==2，利用等差数列的通项公式与对数的运算性质即可得出．‎ ‎（Ⅱ）由（Ⅰ）可得：an=2n，可得=﹣．再利用“裂项求和”方法与数列的单调性即可证明．‎ ‎【解答】（Ⅰ）解：∵f（x1）==2，公差d=2．‎ ‎∴f（xn）=2+2（n﹣1）=2n，‎ ‎∴logaxn=2n，解得xn=a2n．‎ ‎（Ⅱ）证明：由（Ⅰ）可得：an=logaxn=2n，‎ ‎∴===﹣．‎ ‎∴++…+=+…+=1﹣＜1．‎ ‎　‎ ‎20．根据下列算法语句，将输出的A值依次记为a1，a2，…，an，…，a2015；已知函数f（x）=a2sin（ωx+φ）（ω＞0，|φ|＜）的最小正周期是a1，且函数y=f（x）的图象关于直线x=对称．‎ ‎（Ⅰ）求函数y=f（x）表达式；‎ ‎（Ⅱ）已知△ABC中三边a，b，c对应角A，B，C，a=4，b=4，∠A=30°，求f（B）．‎ ‎【考点】伪代码；正弦定理．‎ ‎【分析】（Ⅰ）由已知算法语句可知所求为2015个奇数的和；根据a1=1，a2=4，得到函数的周期，由对称轴x=，结合|φ|＜得到φ，从而求出三角函数解析式；‎ ‎（Ⅱ）由正弦定理计算B，即可求f（B）．‎ ‎【解答】解：（Ⅰ）由已知，当n≥2时，an=1+3+5+…+（2n﹣1）=n2‎ 而a1=1也符合an=n2，知a1=1，a2=4，所以函数y=f（x）的最小正周期为1，所以ω=2π，‎ 则f（x）=4sin（2πx+φ），‎ 又函数y=f（x）的图象关于直线x=对称 所以+φ=kπ+（k∈Z），因为|φ|＜，所以φ=，则f（x）=4sin（2πx+）‎ ‎（Ⅱ）由正弦定理计算，∴sinB=，∴B为或，‎ 可得f（B）=4sin（+）或4sin（+） ‎ ‎　‎ ‎21．某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元．该公司第n年需要付出设备的维修和工人工资等费用an的信息如图．‎ ‎（1）求an；‎ ‎（2）引进这种设备后，第几年后该公司开始获利；‎ ‎（3）这种设备使用多少年，该公司的年平均获利最大？‎ ‎【考点】数列的求和；基本不等式；数列的函数特性．‎ ‎【分析】（1）由题意知，每年的费用是以2为首项，2为公差的等差数列，求得：an=a1+2（n﹣1）=2n．‎ ‎（2）设纯收入与年数n的关系为f（n），则f（n）=20n﹣n2﹣25，由此能求出引进这种设备后第2年该公司开始获利．‎ ‎（3）年平均收入为=20﹣（n+）≤20﹣2×5=10，由此能求出这种设备使用5年，该公司的年平均获利最大．‎ ‎【解答】解：（1）如图，a1=2，a2=4，‎ ‎∴每年的费用是以2为首项，2为公差的等差数列，‎ ‎∴an=a1+2（n﹣1）=2n．‎ ‎（2）设纯收入与年数n的关系为f（n），‎ 则f（n）=21n﹣[2n+×2]﹣25=20n﹣n2﹣25，‎ 由f（n）＞0得n2﹣20n+25＜0，‎ 解得10﹣5＜n＜10+5，‎ 因为n∈N，所以n=2，3，4，…18．‎ 即从第2年该公司开始获利．‎ ‎（3）年平均收入为=20﹣（n+）≤20﹣2×5=10，‎ 当且仅当n=5时，年平均收益最大．‎ 所以这种设备使用5年，该公司的年平均获利最大．‎ ‎　‎ ‎22．设等比数列{an}的前n项和为Sn，已知a1=2，且4S1，3S2，2S3成等差数列．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=|2n﹣5|•an，求数列{bn}的前n项和Tn．‎ ‎【考点】数列的求和；数列递推式．‎ ‎【分析】（Ⅰ）根据4S1，3S2，2S3成等差数列．根据等差中项6S2=4S1+2S3，化简整理求得q=2，写出通项公式；‎ ‎（Ⅱ）讨论当n=1、2时，求得T1=6，T2=10，写出前n项和，采用错位相减法求得Tn．‎ ‎【解答】解：（Ⅰ）∵4S1，3S2，2S3成等差数列，‎ ‎∴6S2=4S1+2S3，‎ 即6（a1+a2）=4a1+2（a1+a2+a3），‎ 则：a3=2a2，q=2，‎ ‎∴；‎ ‎（Ⅱ）当n=1，2时，T1=6，T2=10，‎ 当n≥3，Tn=10+1×23+3×24+…+（2n﹣5）•2n，‎ ‎2Tn=20+1×24+3×25+…+（2n﹣7）×2n+（2n﹣5）×2n+1，‎ 两式相减得：﹣Tn=﹣10+8+2（24+25+…+2n）﹣（2n﹣5）×2n+1，‎ ‎=﹣2+2×﹣（2n﹣5）×2n+1，‎ ‎=﹣34+（7﹣2n）•2n+1，‎ ‎∴Tn=34﹣（7﹣2n）•2n+1．‎ ‎∴．‎ ‎　‎