2020届二轮复习简单的线性规划问题(三)课件（18张）（全国通用）

2020届二轮复习简单的线性规划问题(三)课件（18张）（全国通用）

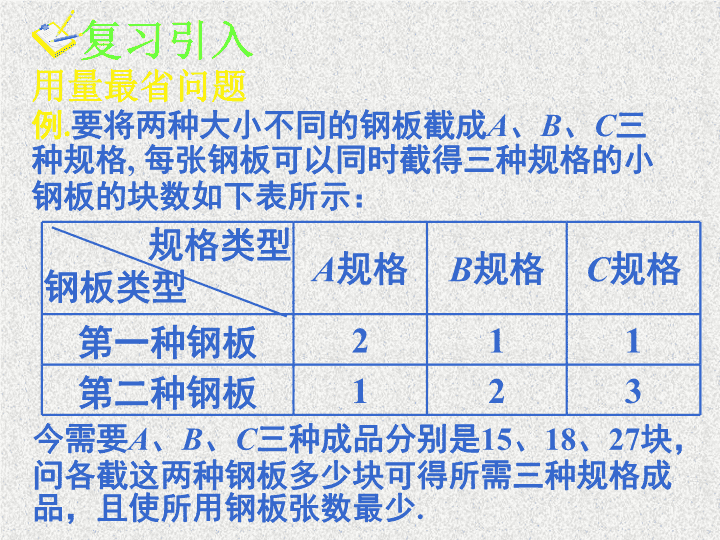
例 . 要将两种大小不同的钢板截成 A 、 B 、 C 三 种规格 , 每张钢板可以同时截得三种规格的小 钢板的块数如下表所示： A 规格 B 规格 C 规格 第一种钢板 2 1 1 第二种钢板 1 2 3 今需要 A 、 B 、 C 三种成品分别是 15 、 18 、 27 块， 问各截这两种钢板多少块可得所需三种规格成 品，且使所用钢板张数最少 . 规格类型 钢板类型 用量最省问题 复习引入 解： 设需截第一种钢板 x 张，第二种钢板 y 张，则 作出可行域： 目标函数为 z ＝ x ＋ y 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 y x O 2 2 4 8 8 18 28 16 复习引入 练习 某公司招收男职员 x 名 ， 女职员 y 名 ， x 和 y 须满足约束条件 : 则 z =10 x +10 y 的最大值是 : A. 80 B. 85 C. 90 D.95 ( ) 复习引入 讲授新课 例 1. 设 x , y , z 满足约束条件 求 u ＝ 2 x ＋ 6 y ＋ 4 z 的最大值和最小值 . 讲授新课 例 2. (1) 已知 的取值范围； (2) 设 f ( x ) ＝ a x 2 ＋ b x ，且 1≤ f ( － 1)≤2 ， 2≤ f ( 1)≤4 ，求 f ( － 2) 的取值范围 . 求 t ＝ 4 a － 2 b 练习 教科书 P.91 练习第 2 题． 讲授新课 讲授新课 思考 . 已知△ ABC 的三边长 a 、 b 、 c 满足 b ＋ c ≤2 a ， c ＋ a ≤2 b ，求 的取值范围 . 1. 巩固图解法求线性目标函数的最大 值、最小值的方法； 2. 用画网格的方法求解整数线性规划 问题 . 课堂小结 1. 阅读教科书 P. 88- P. 90 ； 2.《 习案 》 第三十课时 . 课外作业