2014届高三理科数学一轮复习试题选编29：定积分的计算及其应用（学生版）

2014届高三理科数学一轮复习试题选编29：定积分的计算及其应用（学生版）

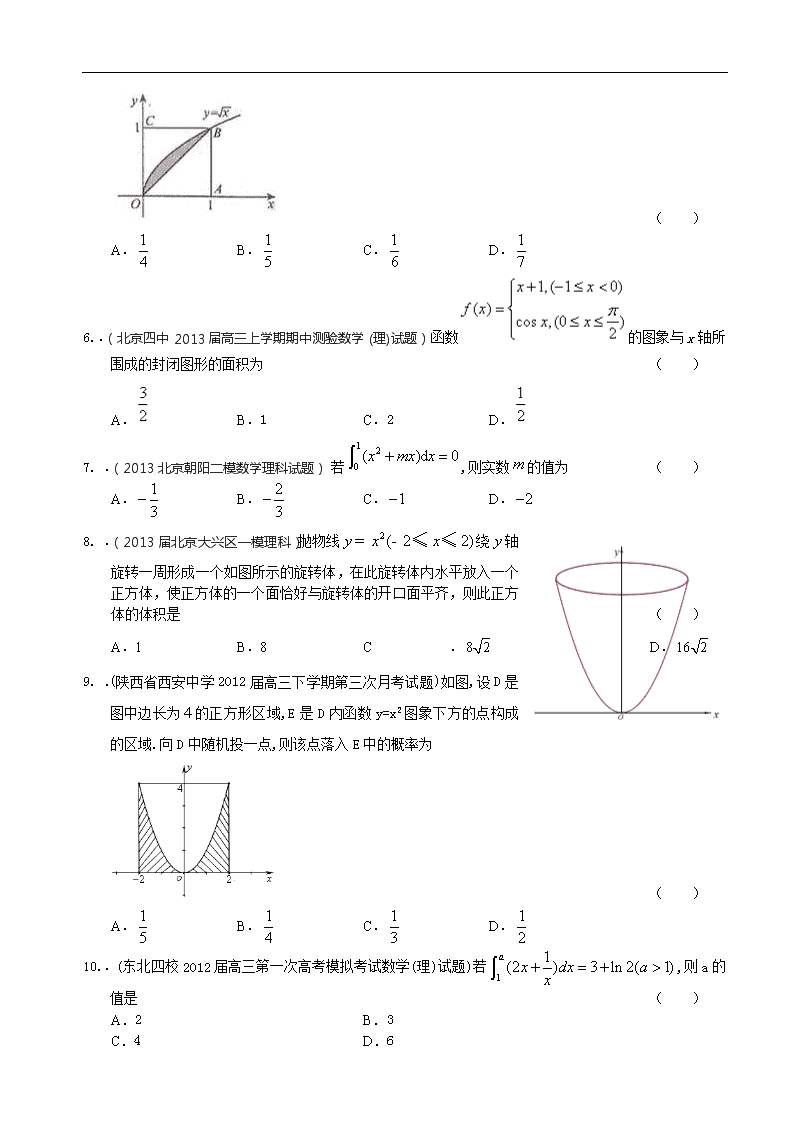
‎2014届高三理科数学一轮复习试题选编29：定积分的计算及其应用 一、选择题 ．(安徽寿县一中2012年高三第四次月考试卷)求由曲线,直线及轴所围成的图形的面积错误的为 （　　）‎ A． B．C．D．‎ ．(江西重点高中协作体第二次联考理科)若函数,则的值为 （　　）‎ A． B． C． D．‎ ．(2011-2012学年厦门市3月份高三数学质量检查试题(理科))如图,已知幂函数的图像过点,则图中阴影部分的面积等于 ‎ ‎ （　　）‎ A． B． C． D． ‎ ．(2012年高考(湖北理))已知二次函数的图象如图所示,则它与轴所围图形的面积为 ‎ y x O 第3题图 ‎ （　　）‎ A． B． C． D． ‎ ．(2012年高考(福建理))如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为 ‎ ‎ （　　）‎ A． B． C． D．‎ ．（北京四中2013届高三上学期期中测验数学(理)试题）函数 的图象与x轴所围成的封闭图形的面积为 （　　）‎ A． B．‎1 ‎C．2 D．‎ ．（2013北京朝阳二模数学理科试题）若,则实数的值为 （　　）‎ A． B． C． D． ‎ ．（2013届北京大兴区一模理科）抛物线绕轴旋转一周形成一个如图所示的旋转体，在此旋转体内水平放入一个正方体，使正方体的一个面恰好与旋转体的开口面平齐，则此正方体的体积是 （　　）‎ A．1 B．‎8 ‎C． D．‎ ．(陕西省西安中学2012届高三下学期第三次月考试题)如图,设D是图中边长为的正方形区域,E是D内函数y=x2图象下方的点构成的区域.向D中随机投一点,则该点落入E中的概率为 ‎ （　　）‎ A． B． C． D．‎ ．(东北四校2012届高三第一次高考模拟考试数学(理)试题)若,则a的值是 （　　）‎ A．2 B．3 ‎ C．4 D．6‎ ．(2013湖北高考数学(理))一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度(的单位:, 的单位:)行驶至停止.在此期间汽车继续行驶的距离(单位;)是 （　　）‎ A． B． C． D．‎ ．（2013北京高考数学（理））直线l过抛物线C: x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于 （　　）‎ A． B．‎2 ‎C． D．‎ 二、填空题 ．（北京市海淀区2013届高三上学期期中练习数学（理）试题）___________.‎ ．（北京市东城区普通高中示范校2013届高三12月综合练习(一)数学理试题）由曲线,直线及轴所围成的图形的面积为______________.‎ ．（北京市海淀区2013届高三5月查缺补漏数学（理））计算____________. ‎ ．(2013湖南高考数学(理))若_________.‎ ．(2012年高考(江西理))计算定积分___________.‎ ．(福建省龙岩市高中毕业班数学3月质量检查(理科))设函数,若, 其中,则=________.‎ ．(2012年高考(山东理))设.若曲线与直线所围成封闭图形的面积为,则______.‎ ．(湖北黄冈中学高三五月模拟)函数在点处的切线与函数围成的图形的面积等于_________.‎ ．(2012年石景山区高三数学一模理科)如图,圆内的正弦曲线与轴围成的区域记为 (图中阴影部分),随机往圆内投一个点,则点落在区域内的概率是_________.‎ ．(2012年高考(上海文))已知函数的图像是折线段ABC,若中A(0,0),B(,1),C(1,0).‎ 函数的图像与x轴围成的图形的面积为_______ .‎ ．（北京市东城区2013届高三上学期期末考试数学理科试题）图中阴影部分的面积等于　 ．‎ ．(惠州市2012届高三一模考试数学(理科)试题解析版)由曲线,围成的封闭图形面积为___________.‎ ．（北京市房山区2013届高三上学期期末考试数学理试题 ） = . ‎ 北京市2014届高三理科数学一轮复习试题选编29：定积分的计算及其应用参考答案 一、选择题 C ‎ C ‎ C ‎ 解析:根据图像可得: ,再由定积分的几何意义,可求得面积为. ‎ 【答案】C ‎ ‎【解析】,故,答案C ‎ A【解析】根据积分的应用可求面积为 ‎ ‎,选A. ‎ B ‎ B C ‎ A ‎ C解:令 ,则.汽车刹车的距离是,故选C. ‎ C 的方程是,所求面积相当于一个矩形面积减去一个积分值:. ‎ 二、填空题 ‎ 【解析】由,解得,即,所以所求面积为 ‎ ‎ ‎ ‎ 3 解: ‎ 【解析】本题考查有关多项式函数,三角函数定积分的应用. ‎ ‎. ‎ ‎ 【解析】由已知得,所以,所以. ‎ ‎ ‎ [解析] 如图1,, ‎ x y A B C ‎1‎ ‎1‎ 图1‎ ‎(O)‎ N x y O D M ‎1‎ P 图2‎ 所以, ‎ 易知,y=xf(x)的分段解析式中的两部分抛物线形状完全相同,只是开口方向及顶点位置不同,如图2,封闭图形MND与OMP全等,面积相等,故所求面积即为矩形ODMP的面积S=. ‎ 【答案】‎ 解：根据积分应用可知所求面积为。‎ 【解析】结合图形可知所求封闭图形的面积为. ‎ ‎