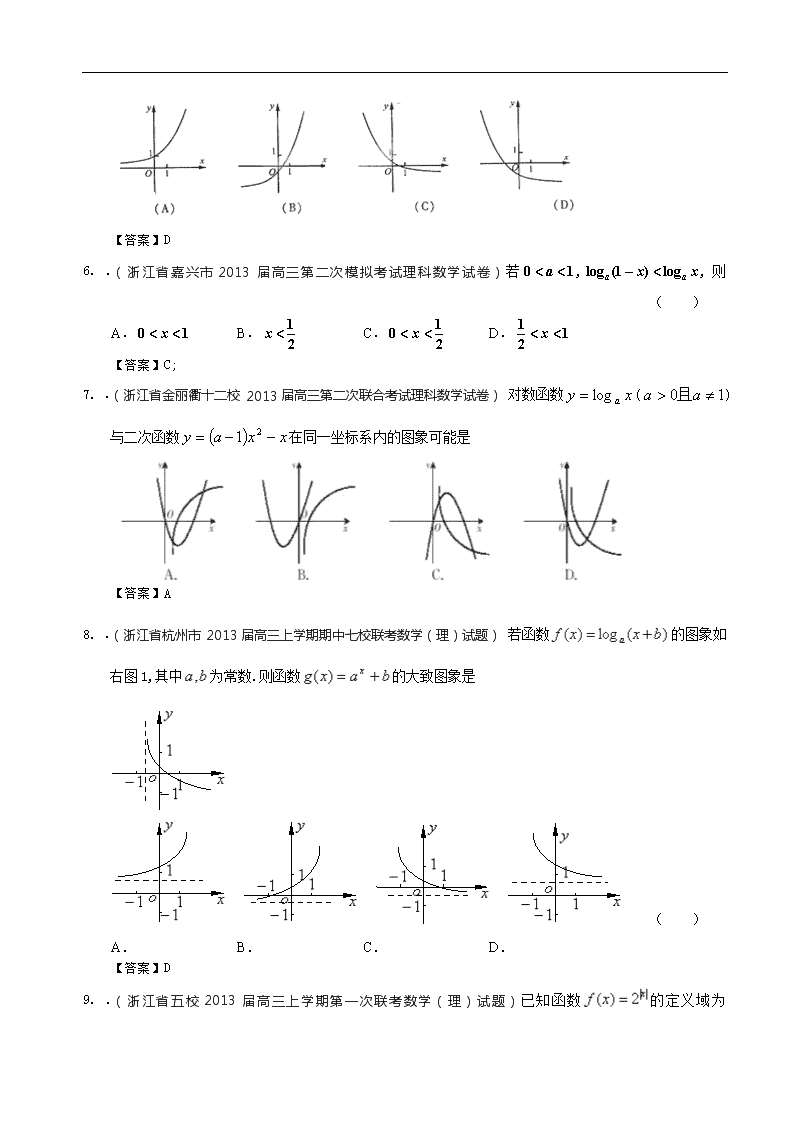浙江省2014届理科数学专题复习试题精选5:指数与指数函数及对数与对数函数(教师版)
浙江省2014届理科数学专题复习试题精选5:指数与指数函数及对数与对数函数
一、选择题
.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))已知为正实数,则 ( )
A. B.
C. D.
【答案】D
.(2013年杭州市第一次高考科目教学质量检测理科数学试题)设函数,则下列结论中正确的是 ( )
A. B.
C. D.
【答案】D解:由题意,,即为偶函数.
故. 显然单调递增.
所以
.(浙江省重点中学2013届高三上学期期中联谊数学(理)试题)设与(且≠2)具有不同的单调性,则与 的大小关系是 ( )
A.M
N D.M≤N
【答案】C
.(浙江省十校联合体2013届高三上学期期初联考数学(理)试题)已知函数f(x)=1-2x, g(x)= x2-4x+3若有f(a)=g(b),则的取值范围为 ( )
A. B. C. D.
【答案】B
.(浙江省宁波市金兰合作组织2013届高三上学期期中联考数学(理)试题)函数的图象可能是
【答案】D
.(浙江省嘉兴市2013届高三第二次模拟考试理科数学试卷)若,,则 ( )
A. B. C. D.
【答案】C;
.(浙江省金丽衢十二校2013届高三第二次联合考试理科数学试卷)对数函数()与二次函数在同一坐标系内的图象可能是
【答案】A
.(浙江省杭州市2013届高三上学期期中七校联考数学(理)试题)若函数的图象如右图1,其中为常数.则函数的大致图象是
( )
A. B. C. D.
【答案】D
.(浙江省五校2013届高三上学期第一次联考数学(理)试题)已知函数的定义域为
,值域为,则在平面直角坐标系内,点的
运动轨迹与两坐标轴围成的图形的面积为 ( )
A. B. C. D.
【答案】 C.
.(2013年杭州市第一次高考科目教学质量检测理科数学试题)设函数的定义域为,值域为,若的最小值为,则实数a的值为 ( )
A. B.或 C. D.或
【答案】D解:由题意,分或两种情况:
(1)时,,此时在上单调递减
故
(2)时,,此时在上单调递增
故
二、填空题
.(浙江省乐清市普通高中2013届高三上学期期末教学质量检测数学(理)试题)方程的解集为________.
【答案】
.(浙江省宁波市十校2013届高三下学期能力测试联考数学(理)试题)已知整数满足,且,则整数组为____________
【答案】
.(浙江省嘉兴市2013届高三上学期基础测试数学(理)试题)若,则的最小值是____________.
【答案】
.(浙江省十校联合体2013届高三上学期期初联考数学(理)试题)已知函数在区间上是增函数,则实数的取值范围是____________
【答案】[,2];
.(浙江省重点中学2013届高三上学期期中联谊数学(理)试题)若函数,(且
)的值域为R,则实数的取值范围是__________;_
【答案】
.(浙江省重点中学协作体2013届高三摸底测试数学(理)试题)已知且,则使方程有解时的的取值范围为______.
【答案】或
三、解答题
.(浙江省杭州市2013届高三上学期期中七校联考数学(理)试题)设函数的定义域为集合,函数()的定义域为集合.
(1)当时,求集合;
(2)若,求实数的取值范围.
【答案】解:(1)由函数有意义,得:,
即或,所以,
当时,函数有意义,得:,
即,,,
(2)由函数()有意义得,
即,,,,
若,则,
或,得或,即
.(浙江省重点中学2013届高三上学期期中联谊数学(理)试题)定义在上的函数,如果满足:对任意,存在常数,
都有成立,则称是上的有界函数,其中称为函数的上界.
已知函数;
(I)当时,求函数在上的值域,并判断函数在上是否为
有界函数,请说明理由;
(Ⅱ)若函数在上是以3为上界的有界函数,求实数的取值范围;
(Ⅲ)已知,函数在上的上界是,求的取值范围.
【答案】解:(I)当时,
因为在上递减,所以,即在的值域为
故不存在常数,使成立
所以函数在上不是有界函数
(Ⅱ)由题意知,在上恒成立.
,
∴ 在上恒成立
∴
设,,,由得 t≥1,
(设,
所以在上递减,在上递增, (单调性不证,不扣分))
在上的最大值为, 在上的最小值为
所以实数的取值范围为
(Ⅲ),
∵ m>0 , ∴ 在上递减,
∴ 即
∵ , ∴ 在上递增,
∴ 即个
①当时,, 此时
②当,即,, 此时 ,
③当时,,此时
综上所述:当时,的取值范围是;
当时,的取值范围是