【数学】2019届人教B版专题13空间中的平行与垂直学案

【数学】2019届人教B版专题13空间中的平行与垂直学案

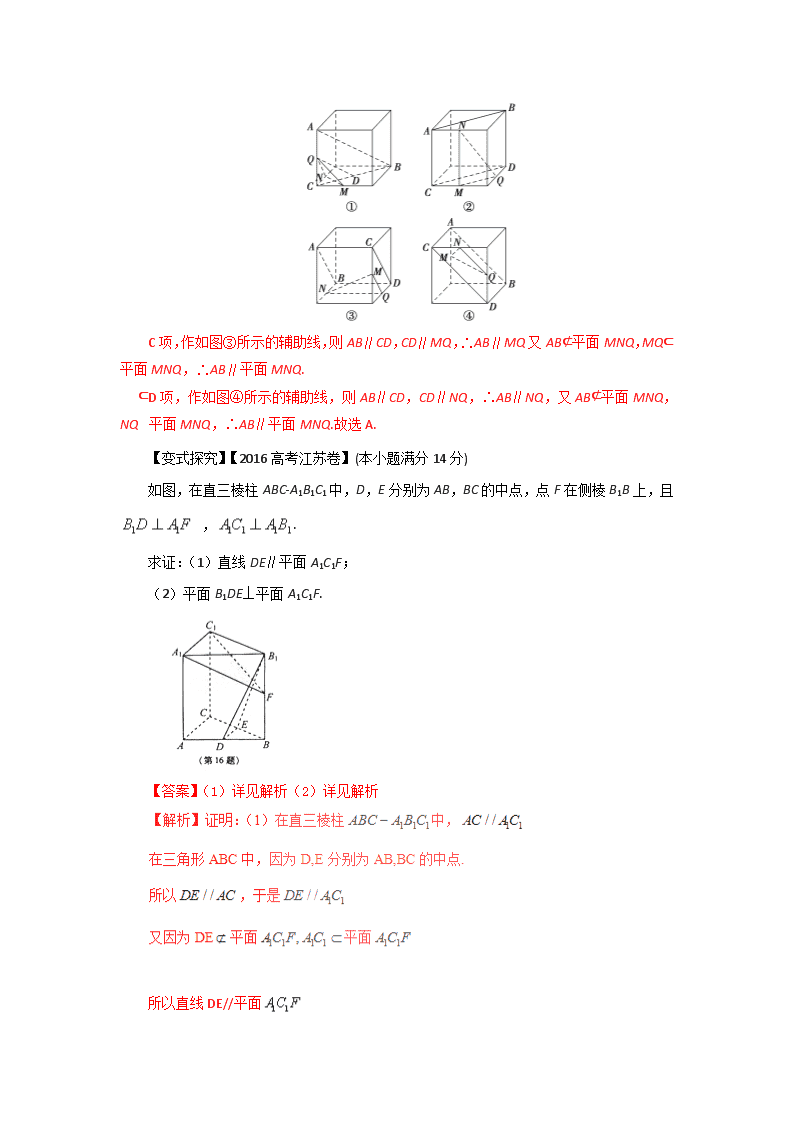
‎【考向解读】 ‎ ‎1.以选择题、填空题的形式考查，主要利用平面的基本性质及线线、线面和面面的判定与性质定理对命题的真假进行判断，属基础题.‎ ‎2.以解答题的形式考查，主要是对线线、线面与面面平行和垂直关系交汇综合命题，且多以棱柱、棱锥、棱台或其简单组合体为载体进行考查，难度中等.‎ ‎【命题热点突破一】 空间线面位置关系的判定 ‎ (1)根据空间线面平行、垂直关系的判定定理和性质定理逐项判断 解决问题；‎ ‎(2)必要时可以借助空间几何模型，如从长方体、四面体等模型中观察线面位置关系，并结合有关定理 进行判断．‎ 例1、(2017·高考全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是(　　)‎ ‎ ‎ C项，作如图③所示的辅助线，则AB∥CD，CD∥MQ，∴AB∥MQ又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ.‎ D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，∴AB∥NQ，又AB⊄平面MNQ，NQ⊂平面MNQ，∴AB∥平面MNQ.故选A. ‎ ‎【变式探究】【2016高考江苏卷】(本小题满分14分)‎ 如图，在直三棱柱ABC-A1B‎1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且 ，.‎ 求证：（1）直线DE∥平面A1C1F；‎ ‎（2）平面B1DE⊥平面A1C1F. ‎ ‎【答案】（1）详见解析（2）详见解析 所以直线DE//平面 ‎（2）在直三棱柱中，‎ 因为平面，所以 又因为 所以平面 因为平面，所以 又因为 所以 因为直线，所以 ‎ ‎【变式探究】(1)若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是(　　)‎ A．l与l1，l2都不相交 B．l与l1，l2都相交 C．l至多与l1，l2中的一条相交 D．l至少与l1，l2中的一条相交 ‎(2)平面α∥平面β的一个充分条件是(　　)‎ A．存在一条直线a，a∥α，a∥β B．存在一条直线a，a⊂α，a∥β C．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α D．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α 答案 (1)D　(2)D 若α∩β＝l，a⊂α，a∥l，b⊂β，b∥l，则a∥β，b∥α，故排除C.故选D. ‎ ‎【特别提醒】‎ 解决空间点、线、面位置关系的组合判断题，主要是根据平面的基本性质、空间位置关系的各种情况，以及空间线面垂直、平行关系的判定定理和性质定理进行判断，必要时可以利用正方体、长方体、棱锥等几何模型辅助判断，同时要注意平面几何中的结论不能完全引用到立体几何中． : | ]‎ ‎【变式探究】 ‎ 已知m，n为两条不同的直线，α，β为两个不重合的平面，给出下列命题：‎ ‎①若m⊥α，n⊥α，则m∥n；‎ ‎②若m⊥α，m⊥n，则n∥α；‎ ‎③若α⊥β，m∥α，则m⊥β；‎ ‎④若m⊥α，m∥β，则α⊥β.‎ A．0 B．1‎ C．2 D．3‎ 答案 C　‎ ‎【命题热点突破二】 空间平行、垂直关系的证明 空间平行、垂直关系证明的主要思想是转化，即通过判定、性质定理将线线、线面、面面之间的平行、垂直关系相互转化．‎ 例2、(2017·高考全国卷Ⅲ)如图，四面体ABCD中，△ABC是正三角形，AD＝CD.‎ ‎(1)证明：AC⊥BD；‎ ‎(2)已知△ACD是直角三角形，AB＝BD.若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．‎ ‎ ‎ ‎【变式探究】【2016高考江苏卷】(本小题满分14分)‎ 如图，在直三棱柱ABC-A1B‎1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且 ，.‎ 求证：（1）直线DE∥平面A1C1F；‎ ‎（2）平面B1DE⊥平面A1C1F. ‎ ‎【答案】（1）详见解析（2）详见解析 ‎（2）在直三棱柱中， ‎ 因为平面，所以 又因为 所以平面 因为平面，所以 又因为 所以 因为直线，所以 ‎ ‎【变式探究】如图，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.‎ ‎ (1)证明：BC∥平面PDA；‎ ‎(2)证明： BC⊥PD；‎ ‎(3)求点C到平面PDA的距离．‎ 在Rt△PED中，PE＝＝＝.‎ 因为平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，PE⊂平面PDC，‎ 所以PE⊥平面ABCD，‎ 由(2)知：BC⊥平面PDC，‎ 由(1)知：BC∥AD，‎ 所以AD⊥平面PDC，‎ 因为PD⊂平面PDC，‎ 所以AD⊥PD.设点C到平面PDA的距离为h，‎ 因为V三棱锥CPDA＝V三棱锥PACD，‎ 所以S△PDA·h＝S△ACD·PE， ‎ 即h＝＝＝，‎ 所以点C到平面PDA的距离是. ‎ ‎【特别提醒】　垂直、平行关系的基础是线线垂直和线线平行，常用方法如下：‎ ‎(1)证明线线平行常用的方法：一是利用平行公理，即证两直线同时和第三条直线平行；二是利用平行四边形进行平行转换；三是利用三角形的中位线定理证线线平行；四是利用线面平行、面面平行的性质定理进行平行转换．‎ ‎(2)证明线线垂直常用的方法：①利用等腰三角形底边中线即高线的性质；②勾股定理；③线面垂直的性质：即要证两线垂直，只需证明一线垂直于另一线所在的平面即可，l⊥α，a⊂α⇒l⊥a.‎ ‎【变式探究】‎ 如图所示，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．‎ 求证：(1)AF∥平面BCE；‎ ‎(2)平面BCE⊥平面CDE.[ : + ]‎ ‎∵DE⊥平面ACD，AF⊂平面ACD，‎ ‎∴DE⊥AF.‎ 又CD∩DE＝D，故AF⊥平面CDE.‎ ‎∵BG∥AF，∴BG⊥平面CDE. ‎ ‎∵BG⊂平面BCE，∴平面BCE⊥平面CDE.‎ ‎【命题热点突破三】 平面图形的折叠问题 平面图形经过翻折成为空间图形后，原有的性质有的发生变化、有的没有发生变化，这些发生变化和没有发生变化的性质是解决问题的关键．一般地，在翻折后还在一个平面上的性质不发生变化，不在同一个平面上的性质发生变化，解决这类问题就是要根据这些变与不变，去研究翻折以后的空间图形中的线面关系和各类几何量的度量值，这是化解翻折问题的主要方法．‎ 例3、【2016高考新课标2文数】如图，菱形的对角线与交于点，，点分别在上，，交于点．将沿折到位置，．‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）求二面角的正弦值．‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ 于是，‎ 故. ‎ 又，而，‎ 所以.‎ ‎【变式探究】如图(1)，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图(2)．‎ ‎(1)求证：DE∥平面A1CB；‎ ‎(2)求证：A1F⊥BE；‎ ‎(3)线段A1B上是否存在点Q，使A1C⊥平面DEQ？请说明理由．‎ ‎ ‎ ‎(3)解　线段A1B上存在点Q，使A1C⊥平面DEQ.‎ 理由如下：‎ 如图，分别取A1C，A1B的中点P，Q，则PQ∥BC.‎ 又因为DE∥BC，‎ 所以DE∥PQ.‎ 所以平面DEQ即为平面DEP.‎ 由(2)知，DE⊥平面A1DC，‎ 所以DE⊥A1C. ‎ 又因为P是等腰三角形DA1C底边A1C的中点，‎ 所以A1C⊥DP.所以A1C⊥平面DEP.‎ 从而A1C⊥平面DEQ.‎ 故线段A1B上存在点Q，使得A1C⊥平面DEQ.‎ ‎【特别提醒】(1)折叠问题中不变的数量和位置关系是解题的突破口；(2)存在探索性问题可先假设存在，然后在此前提下进行逻辑推理，得出矛盾或肯定结论．‎ ‎【变式探究】如图(1)，四边形ABCD为矩形，PD⊥平面ABCD，AB＝1，BC＝PC＝2，作如图(2)折叠，折痕EF∥DC.其中点E，F分别在线段PD，PC上，沿EF折叠后点P叠在线段AD上的点记为M，并且MF⊥CF.‎ ‎(1)证明：CF⊥平面MDF；[ : _ _ ]‎ ‎(2)求三棱锥M－CDE的体积．‎ 所以MD＝＝＝.‎ S△CDE＝DE·DC＝××1＝.‎ 故VM－CDE＝MD·S△CDE＝××＝.‎ ‎【高考真题解读】‎ ‎1．(2017·高考全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是(　　)‎ ‎∴AB∥平面MNQ.‎ D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，∴AB∥NQ，又AB⊄平面MNQ，NQ⊂平面MNQ，∴AB∥平面MNQ.故选A.‎ ‎2．(2017·全国卷Ⅲ)在正方体ABCDA1B‎1C1D1中，E为棱CD的中点，则(　　)‎ A．A1E⊥DC1 B．A1E⊥BD C．A1E⊥BC1 D．A1E⊥AC 答案：C ‎3．(2017·高考全国卷Ⅲ)如图，四面体ABCD中，△ABC是正三角形，AD＝CD.‎ ‎(1)证明：AC⊥BD；‎ ‎(2)已知△ACD是直角三角形，AB＝BD.若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．‎ 解：(1)证明：如图，取AC中点O，连OD，OB ‎∵AD＝CD，O为AC中点，‎ ‎∴AC⊥OD，‎ 又∵△ABC是等边三角形，‎ ‎∴AC⊥OB，‎ 又∵OB∩OD＝O，∴AC⊥平面OBD，BD⊂平面OBD，‎ ‎∴AC⊥BD.‎ ‎(2)设AD＝CD＝2，∴AC＝2，AB＝BC＝2，‎ 又∵AB＝BD，∴BD＝2，‎ ‎∴△ABD≌△CBD，∴AE＝EC，‎ 又∵AE⊥EC，AC＝2，‎ ‎∴AE＝EC＝2，‎ 在△ABD中，设DE＝x，根据余弦定理cos∠ADB＝＝ ‎＝＝.‎ 解得x＝，∴点E是BD的中点，则VDACE＝VEACE，‎ ‎∴＝1∶1.‎ ‎4.(2017·全国卷Ⅱ)如图，四棱锥PABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝BC＝AD，∠BAD＝∠ABC＝90°.‎ ‎(1)证明：直线BC∥平面PAD；‎ ‎(2)若△PCD的面积为2，求四棱锥PABCD的体积．‎ 设BC＝x，则CM＝x，CD＝x，PM＝x，PC＝PD＝2x，取CD的中点N，连接PN.‎ 则PN⊥CD，所以PN＝x.‎ 因为△PCD的面积为2，‎ 所以×x×x＝2，解得x＝2或x＝－2(舍去)．(10分)‎ 于是AB＝BC＝2，AD＝4，PM＝2.‎ 所以四棱锥PABCD的体积V＝××2＝4.(12分)‎ ‎1.【2016高考新课标2文数】 是两个平面，是两条直线，有下列四个命题：‎ ‎（1）如果，那么.‎ ‎（2）如果，那么.‎ ‎（3）如果，那么.‎ ‎（4）如果，那么与所成的角和与所成的角相等.‎ 其中正确的命题有 ． (填写所有正确命题的编号）‎ ‎【答案】②③④‎ ‎2.【2016高考浙江文数】如图，在△ABC中，AB=BC=2，∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是 .‎ ‎【答案】‎ ‎【解析】中，因为，所以.‎ 由此可得，将ABD沿BD翻折后可与PBD重合，无论点D在任何位置，只要点D的位置确定，当平面PBD⊥平面BDC时，四面体PBCD的体积最大（欲求最大值可不考虑不垂直的情况）.‎ 过作直线的垂线，垂足为.设，则，‎ 即，解得.‎ 而的面积.‎ 当平面PBD⊥平面BDC时：‎ 四面体的体积.‎ 观察上式，易得，当且仅当，即 时取等号，同时我们可以发现当时，取得最小值，故当时，四面体的体积最大，为 ‎ ‎3.【2016高考新课标1卷】平面过正方体ABCD-A1B‎1C1D1的顶点A,//平面CB1D1,平面ABCD=m,平面AB B‎1A1=n,则m、n所成角的正弦值为 ‎(A) (B) (C) (D)‎ ‎【答案】A ‎4.【2016高考新课标3文数】在封闭的直三棱柱内有一个体积为的球，若，，，，则的最大值是（ ）‎ ‎（A）4π （B） （C）6π （D） ‎ ‎【答案】B ‎【解析】要使球的体积最大，必须球的半径最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径取得最大值，此时球的体积为 ‎，故选B．‎ ‎1．(2015·安徽，5)已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是(　　)‎ A．若α，β垂直于同一平面，则α与β平行 B．若m，n平行于同一平面，则m与n平行 C．若α，β不平行，则在α内不存在与β平行的直线 D．若m，n不平行，则m与n不可能垂直于同一平面 答案　D ‎2．(2015·浙江，8)如图，已知△ABC，D是AB的中点，沿直线CD将△ACD翻折成△A′CD，所成二面角A′－CD－B的平面角为α，则(　　)‎ A．∠A′DB≤α 　　　 B．∠A′DB≥α ‎ C．∠A′CB≤α 　　　 D．∠A′CB≥α 解析　极限思想：若α＝π，则∠A′CB＜π，排除D；若α＝0，如图，则∠A′DB，∠A′CB都可以大于0，排除A，C.故选B.‎ 答案　B ‎3．(2015·浙江，13)如图，三棱锥A－BCD中，AB＝AC＝BD＝CD＝3，AD＝BC＝2，点M，N分别是AD，BC的中点，则异面直线AN，CM所成的角的余弦值是________．‎ 解析　连接DN，作DN的中点O，连接MO，OC.在△AND中．M为AD的中点，则OM綉AN.所以异面直线AN，CM所成角为∠CMO，在△ABC中，AB＝AC＝3，BC＝2，则AN＝2，∴OM＝.在△ACD中，同理可知CM＝2，在△BCD中，DN＝2，在Rt△ONC中，ON＝，CN＝1∴OC＝.在△CMO中，由余弦定理cos∠CMO＝＝＝.‎ 答案　 ‎4．(2015·江苏，16)如图，在直三棱柱ABC－A1B1C1中，已知AC⊥BC，BC＝CC1.设AB1的中点为D，B1C∩BC1＝E.‎ 求证：(1)DE∥平面AA1C1C；‎ ‎(2)BC1⊥AB1.‎ 所以矩形BCC1B1是正方形，‎ 因此BC1⊥B1C.‎ 因为AC，B1C⊂平面B1AC，AC∩B1C＝C，‎ 所以BC1⊥平面B1AC.‎ 又因为AB1⊂平面B1AC，‎ 所以BC1⊥AB1. ‎ ‎5．(2015·新课标全国Ⅱ，19)如图，长方体ABCD－A1B1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形．‎ ‎(1)在图中画出这个正方形(不必说明画法和理由)；‎ ‎ (2)求直线AF与平面α所成角的正弦值．‎ 所以AF与平面EHGF所成角的正弦值为. ‎ ‎6．(2015·新课标全国Ⅰ，18)如图，四边形ABCD为菱形，∠ABC＝120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE＝2DF，AE⊥EC. ‎ ‎ (1)证明：平面AEC⊥平面AFC，‎ ‎(2)求直线AE与直线CF所成角的余弦值．‎ ‎ ‎ ‎(2)解　如图，以G为坐标原点，分别以，的方向为x轴，y轴正方向，||为单位长，建立空间直角坐标系G－xyz，由(1)可得A(0，－，0)，E(1，0，)，F，C(0，，0)，所以＝(1，，)，＝.‎ 故cos〈，〉＝＝－.‎ 所以直线AE与直线CF所成角的余弦值为.‎ ‎7．(2014·江苏，16)如图，在三棱锥P－ABC中，D，E，F分别为棱PC，AC，AB的中点．已知PA⊥AC，PA＝6，BC＝8，DF＝5.‎ 求证：(1)直线PA∥平面DEF；‎ ‎(2)平面BDE⊥平面ABC.‎ ‎ ‎ ‎8．(2014·新课标全国Ⅱ，18)如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．‎ ‎(1)证明：PB∥平面AEC；‎ ‎(2)设二面角D－AE－C为60°，AP＝1，AD＝，求三棱锥E－ACD的体积．‎ ‎ ‎ 如图，以A为坐标原点，的方向为x轴的正方向，||为单位长，建立空间直角坐标系A－xyz，则D(0，，0)，E，＝.‎ 设B(m，0，0)(m>0)，则C(m，，0)，＝(m，，0)．‎ 设n1＝(x，y，z)为平面ACE的法向量，‎ 则即 可取n1＝.‎ 又n2＝(1，0，0)为平面DAE的法向量，由题设知|cos〈n1，n2〉|＝，即＝，解得m＝.因为E为PD的中点，所以三棱锥E－ACD的高为，三棱锥E－ACD的体积V＝××××＝.‎