江苏省南通市2020届高三高考考前模拟卷（五）数学Ⅰ试题含附加题

江苏省南通市2020届高三高考考前模拟卷（五）数学Ⅰ试题含附加题

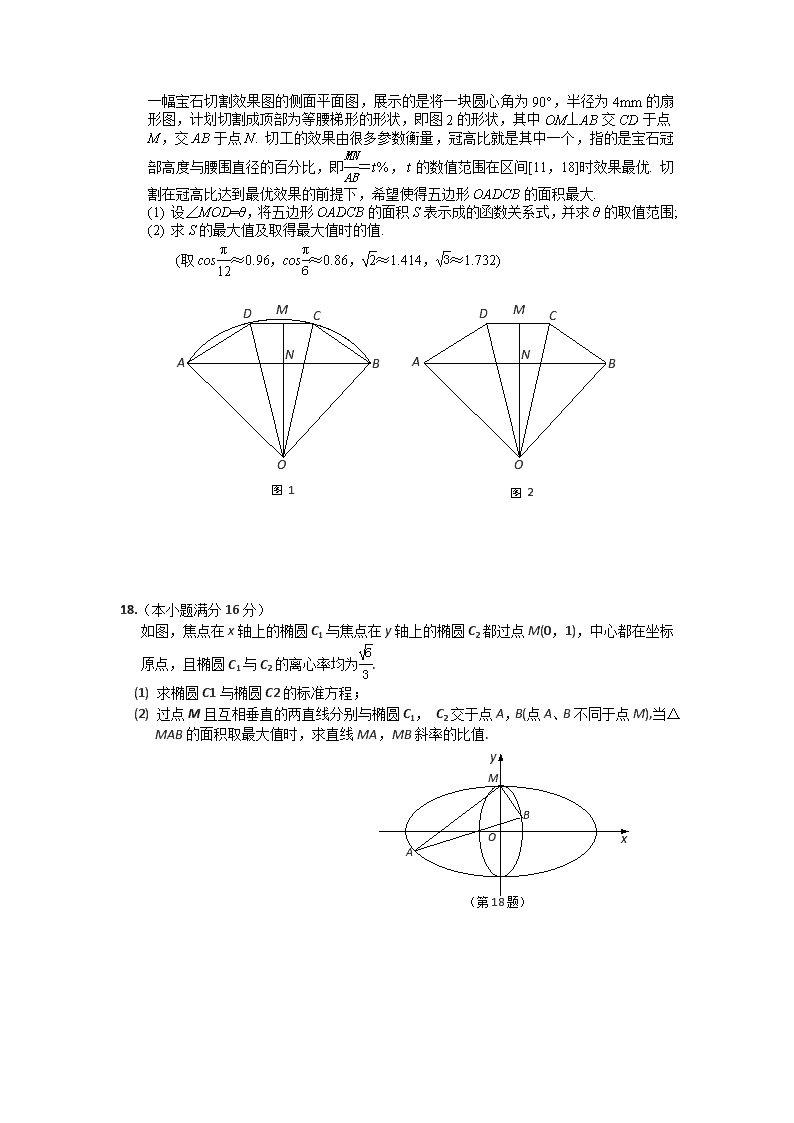
南通市2020届高考考前模拟卷（五）‎ 数学Ⅰ ‎（南通数学学科基地命题）‎ 一、填空题:本大题共14小题,每小题5分,共70分．请把答案直接填写在答题卡相应位置上.‎ ‎1. 已知全集U=R，集合A={x｜3≤x＜7}，B={x｜x2－7x+10＜0}，则A∩B＝ ▲ .‎ ‎2. 已知a∈R，复数满足=1+ai且虚部为－1(i为虚数单位)，则a＝ ▲ .‎ ‎3. 如图是某个容量为100的样本的频率分布直方图，则数据在区间[6，10)上的频数是 ▲ .‎ ‎4. 如图是一个算法流程图，则输出的S的值为 ▲ .‎ N ‎（第4题）‎ 输出S 结束 a≥3‎ a←5，S←1‎ 开始 Y a←a－1‎ S←S×a ‎（第3题）‎ ‎0.200‎ ‎0.025‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎0.075‎ ‎2‎ ‎0.050‎ 数据 ‎ ‎ ‎5. 记函数f(x)= 的定义域为D，若在区间[－5，5]上随机取一个数x，则x∈D 的概率为 ▲ .‎ ‎6. 在各项都是正数的等比数列{an}中，a2，a3，a1成等差数列，则的值是 ▲ .‎ ‎7. 已知函数f(x)= sin(ωx+φ) (ω>0，0<φ<π)的最小正周期是π，若将该函数的图象向右平移个 单位长度后得到的图象关于原点对称，则函数的解析式f(x)= ▲ .‎ ‎8. 已知不等式组表示的平面区域为S，若点P(x，y)∈S，且z=2x+y的最大值 为9，则实数a的值为 ▲ .‎ ‎9. 已知P是以F1，F2为左，右焦点的双曲线－＝1(a＞0，b＞0)的右支上的一点，且满足・=0，tan∠P F1F2=，则此双曲线的离心率为 ▲ .‎ C1‎ D1‎ B1‎ A1‎ P A D C B Q ‎（第10题）‎ ‎10. 如图，在正方体ABCD－A1B1C1D1中，棱长为2，P为 AA1的中点，Q为CC1的中点，则三棱锥B－PQD的体 积为 ▲ .‎ ‎11. 若圆C:x2＋y2－2x＋4y－3=0关于直线2ax＋by＋6=0对 称，则由点(a，b)向圆C所作切线长的最小值是 ▲ .‎ ‎12. 在△ABC中，角A,B,C所对的边分别为a,b,c，已知C=，若2｜－｜=4，则△ABC 面积的最大值为 ▲ .‎ ‎13. 已知函数f(x)=ax＋3＋|2x2＋(4－a)x－1|的最小值为2，则a＝ ▲ .‎ ‎14. 设函数f1(x)= x2，f2(x)=2（x－x2），f3(x)= |sin2πx|. 取ti =，i=0，1，2，…，2019，‎ Sk=| fk(t1)－fk(t0)|＋| fk(t2)－fk(t1)|＋…＋| fk(t2019)－fk(t2018)|，k=1，2，3，‎ 则S1，S2，S3的大小关系为 ▲ . (用“<”连接)‎ 二、解答题：本大题共6小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15.（本小题满分14分）‎ ‎(第15题)‎ E F B D A C 如图,在四边形ABCD中，AB∥CD，∠ABD=30°，AB=2CD=2AD，DE⊥平面ABCD，EF∥BD，且EF=BD.‎ 求证：(1) DE∥平面ACF;‎ ‎(2)平面ADE⊥平面BDEF.‎ ‎16.（本小题满分14分）‎ 在△ABC中，内角A,B,C所对的边分别为a,b,c，且△ABC的面积S满足S=・=1.‎ (1) 若求角A的值；‎ ‎ (2) 若BC边上的中线长为，求a的值.‎ ‎17.（本小题满分14分）‎ 国家提倡工匠精神，球宝行业对宝石的切割力求完美，以更好地展现宝石的魅力. 如图1是 一幅宝石切割效果图的侧面平面图，展示的是将一块圆心角为90°，半径为4mm的扇形图，计划切割成顶部为等腰梯形的形状，即图2的形状，其中OM⊥AB交CD于点M，交AB于点N. 切工的效果由很多参数衡量，冠高比就是其中一个，指的是宝石冠部高度与腰围直径的百分比，即＝t%，t的数值范围在区间[11，18]时效果最优. 切割在冠高比达到最优效果的前提下，希望使得五边形OADCB的面积最大.‎ ‎(1) 设∠MOD=θ，将五边形OADCB的面积S表示成的函数关系式，并求θ的取值范围;‎ ‎(2) 求S的最大值及取得最大值时的值.‎ ‎(取cos≈0.96，cos≈0.86，≈1.414，≈1.732)‎ 图 2‎ D M N C B O A 图 1‎ D M N C B O A ‎18.（本小题满分16分）‎ 如图，焦点在x轴上的椭圆C1与焦点在y轴上的椭圆C2都过点M(0，1)，中心都在坐标原点，且椭圆C1与C2的离心率均为.‎ ‎(1) 求椭圆C1与椭圆C2的标准方程；‎ x O y B A M ‎（第18题）‎ ‎(2) 过点M且互相垂直的两直线分别与椭圆C1， C2交于点A，B(点A、B不同于点M),当△MAB的面积取最大值时，求直线MA，MB斜率的比值.‎ ‎19.（本小题满分16分）‎ 已知函数f(x)＝(ax2+x+1)ex，其中e是自然对数的底数，a∈R.‎ ‎(1) 当a＝2时，求f(x)的极值;‎ ‎(2) 写出函数f(x)的单调增区间;‎ ‎(3) 当a＝0时，在y轴上是否存在点P，过点P恰能作函数f(x)图象的两条切线?若存在，求出所有这样的点; 若不存在，请说明理由.‎ ‎20.（本小题满分16分）‎ 已知n∈N*且3，如果数列{an}满足:对于任意的i=1，2，…，n，均有ai<，其中S= a1+‎ ‎ a2+…+an，那么称数列{an}为“紧密数列” .‎ ‎(1) 若“紧密数列”{an}:a1,a2,a3,a4为等差数列，a1=2，求数列{an}的公差d的取值范围;‎ ‎(2) 数列{an}: a1, a2…, an为“紧密数列”，求证:对于任意互不相等的m,n,k∈{1,2,3,…n},‎ 均有am+an＞ak;‎ ‎(3) 数列{an}: a1, a2, … , an为“紧密数列”，对于任意的i=1,2,…,n，a∈Z，且ai+1≠ai ‎(1≤i≤n－1)成立，求S的最小值Tn.‎ 南通市2020届高考考前模拟卷（五）‎ 数学Ⅱ(附加题)‎ ‎21．【选做题】本题包括A、B、C三小题，请选定其中两小题，并在相应的答题区域内作答，若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．‎ A．[选修4－2：矩阵与变换]（本小题满分10分）‎ 设点(x，y)在矩阵M对应变换作用下得到点(3x，x＋y)‎ ‎(1) 求矩阵M;‎ ‎(2) 若直线l:x－y＝2在矩阵M对应变换作用下得到直线l′，求直线l′的方程.‎ B．[选修4－4：坐标系与参数方程]（本小题满分10分）‎ 在极坐标系中，求点到曲线ρcosθ上点的距离的最大值.‎ C．[选修4－5：不等式选讲]（本小题满分10分）‎ 设x，y，z均为正实数，且x＋y＋z=4，求证：＋＋的最小值.‎ ‎【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写 出文字说明、证明过程或演算步骤．‎ ‎22．（本小题满分10分）‎ 某校模仿《中国诗词大会)节目举办学校诗词大会，进入正赛的条件：电脑随机抽取10首古诗，参赛者需背完且能够正确背通8首及以上的进入正赛. 若学生甲参赛，他背通每一首古诗的正确的概率均为.‎ ‎(1) 求甲进入正赛的概率;(取≈0.013，结果取两位有效数字)‎ ‎(2) 若进入正赛，则采用积分淘汰制,规则:电脑随机抽取4首古诗，每首古诗背通正确加2分，错误减1分由于难度增加:甲背诵每首古诗正确的概率为，求甲在正赛中积分X的概率分布列及数学期望.‎ ‎23．（本小题满分10分）‎ 设正项数列{an}满足：a2=，且对于∀n∈N*，都有＜an＋an+1＜，且∈N*.‎ ‎ (1) 求a1，a3;‎ ‎(2) 求数列{an}的通项公式.‎ 南通市2020届高考考前模拟卷（五）‎ 试题Ⅰ参考答案(详细答案见教参)‎ 一、填空题：本大题共14小题，每小题5分，共70分．‎ ‎1、答案：[ 3，5)‎ ‎2、答案： －2‎ ‎3、答案： 70‎ ‎4、答案： 60‎ ‎5、答案： ‎6、答案： ‎7、答案：sin ‎8、答案：3‎ ‎9、答案： ‎10、答案： ‎11、答案： ‎12、答案：2 ‎13、答案： ‎14、答案：S2＜S1＜ S3‎ ‎(第15答)‎ E F B D A C 二、解答题（共90分）‎ ‎15、（本小题满分14分）‎ ‎ （略,见图）‎ ‎16、（本小题满分14分）‎ ‎（1）A=；‎ ‎（2）a=.‎ ‎17、（本小题满分14分）‎ ‎（1）[，];‎ ‎（2）θ= ；‎ ‎18、（本小题满分16分）‎ ‎（1）3x2＋y2＝1;‎ ‎（2）.‎ ‎19、（本小题满分16分） ‎（1）e- ;‎ ‎（2）当a＜0时， f(x)的单调增区间(－2，－ )；‎ ‎ 当a＝0时， f(x)的单调增区间(－2，＋∞)；‎ ‎ 当0＜a＜时， f(x)的单调增区间(－∞，－)；‎ ‎ 当a＝时， f(x)的单调增区间(－∞，＋∞)；‎ ‎ 当a＞时， f(x)的单调增区间(－∞，－2)和(－，＋∞)；‎ ‎（3）在y轴上存在点P恰能作曲线的两条切线，点P的纵坐标的取值范围为[0，1）∪｛-5e-3｝.‎ ‎20、（本小题满分16分）‎ ‎ （略）‎ 数学Ⅱ(附加题)‎ ‎21．【选做题】本题包括A、B、C三小题，请选定其中两小题，并在相应的答题区域内作答，若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．‎ A．[选修4－2：矩阵与变换]（本小题满分10分）‎ 答案：M= B．[选修4－4：坐标系与参数方程]（本小题满分10分）‎ 答案：2＋ C．[选修4－5：不等式选讲]（本小题满分10分）‎ 答案： ‎【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写 出文字说明、证明过程或演算步骤．‎ ‎22．（本小题满分10分）‎ ‎（1）0.3 ;‎ ‎（2）E（X）=2.‎ ‎23．（本小题满分10分）‎ ‎（1）a3=;‎ ‎（2）an= (n∈N*).‎