四川省宜宾市南溪二中2019-2020学年高二上学期期中考试数学试卷

四川省宜宾市南溪二中2019-2020学年高二上学期期中考试数学试卷

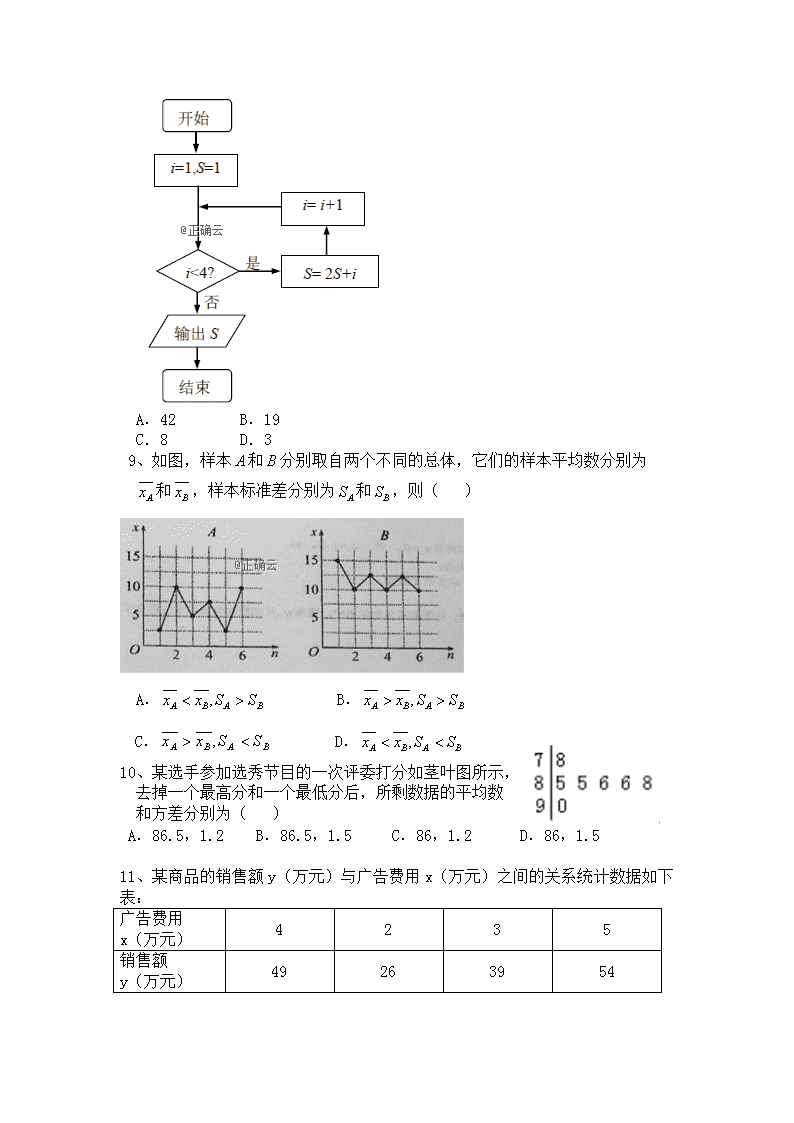
数学 考号：__________ 姓名：__________ 班级：__________ 分数：__________‎ ‎（试卷总分150分，考试时间120分钟）‎ 一、选择题（每题5分，共60分）‎ ‎1、已知两点A（2，1），B（3，3），则直线AB的斜率为（ ）‎ A.2 B. C. D.‎ ‎2、直线的倾斜角为（ ）‎ A. B. C. D.‎ ‎3、过点，且与直线垂直的直线方程为（ ）‎ A. B.‎ C. D.‎ ‎4、某校高三年级有男生500人，女生400人，为了解该年级学生的健康情况，从男生中任意抽取25人，从女生中任意抽取20人进行调查.这种抽样方法是（ ）‎ A．简单随机抽样法 B．抽签法 C．随机数表法 D．分层抽样法 ‎5、给出下列四个命题：‎ ‎①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件 ‎②“当为某一实数时可使”是不可能事件 ‎③“明天拉萨要下雨”是必然事件 ‎④“从100个灯泡中取出5个，5个都是次品”是随机事件 其中正确命题的个数是（ ）‎ A．0 B．1 C．2 D．3‎ ‎6、已知圆，直线，则被圆所截得的弦长为（ ）‎ A. B. 2 C. D. 1‎ ‎7、若圆关于直线 对称，则直线的斜率是（ ）‎ A．6 B． C． D．‎ ‎8、执行如右图所示的程序框图，‎ 输出的值为（ ）‎ A．42 B．19 ‎ ‎ C．8 D．3‎ ‎ 9、如图，样本和分别取自两个不同的总体，它们的样本平均数分别为 和，样本标准差分别为和，则（ ）‎ A． B． ‎ ‎ C． D．‎ ‎10、某选手参加选秀节目的一次评委打分如茎叶图所示，‎ 去掉一个最高分和一个最低分后，所剩数据的平均数 和方差分别为（ ）‎ A．86.5，1.2 B．86.5，1.5 C．86，1.2 D．86，1.5‎ ‎11、某商品的销售额y（万元）与广告费用x（万元）之间的关系统计数据如下表：‎ 广告费用 x（万元）‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额 y（万元）‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 由表中数据算出线性回归方程中的=9.4，据此估计该商品广告费用为6万元时销售额约为（ ）万元．‎ A．63.6 B．64.2 C．65.1 D．65.5‎ ‎12、若实数满足的取值范围为（ ）‎ A. B. C. D.‎ 二、填空题（每题5分，共20分）‎ ‎13、如果对任何实数k，直线（3＋k）x＋（1-2k）y＋1＋5k=0都过一个定点A，那么点A的坐标是 ．‎ ‎14、已知点A（﹣4，﹣5），B（6，﹣1），则以线段AB为直径的圆的方程为 ．‎ ‎15、某单位有名职工，现采用系统抽样方法抽取人做问卷调查，将人按，…随机编号，则抽取的21人中，编号落入区间的人数为 ．‎ ‎16、已知圆，直线.给出下面四个命题：‎ ‎①对任意实数和，直线和圆有公共点；‎ ‎②对任意实数，必存在实数，使得直线和圆相切；‎ ‎③对任意实数，必存在实数，使得直线和圆相切；‎ ‎④存在实数和，使得圆上有一点到直线的距离为.‎ 其中正确的命题是 （写出所有正确命题的编号）. ‎ 三、解答题（共70分）‎ ‎17（10分）对某校高二年级学生参加社区服务次数进行统计，随机抽取名学生作为样本，得到这名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：‎ ‎（1）求出表中M，p及图中的值；‎ ‎（2）若该校高二学生有人，试估计该校高二学生参加社区服务的次数在区间内的人数；‎ p m M ‎ ‎ ‎18、（12分）为了了解某小区2000户居民月用水量使用情况，通过随机抽样获得了100户居民的月用水量.下图是调查结果的频率分布直方图.‎ ‎（1）并根据频率直方图估计某小区200户居民月用水量使用大于3的户数；‎ ‎（2）利用频率分布直方图估计该样本的众数和中位数（保留到0.001）‎ ‎19、（12分）将一枚质地均匀的骰子先后抛掷2次，观察向上的点数，‎ ‎（1）求点数之和是6的概率；‎ ‎（2）两数之积不是4的倍数的概率．‎ ‎20、（12分）某中学调查了某班全部45名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）‎ 参加书法社团 未参加书法社团 参加演讲社团 未参加演讲社团 ‎（1）从该班随机选1名同学，求该同学至少参加上述一个社团的概率；‎ ‎（2）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学,3名女同学，现从这5名男同学和3名女同学中各随机选1人，求被选中且未被选中的概率.‎ ‎21、（12分）直线过点.‎ ‎（1）若直线与直线平行，求直线的方程；‎ ‎（2）若点到直线的距离为1，求直线的方程.‎ ‎22、（12分）在平面直角坐标系中，已知半径为的圆，圆心在轴正半轴上，且与直线相切.‎ ‎（1）求圆的方程；‎ ‎（2）在圆上，是否存在点，满足，其中，点的坐标是.若存在，指出有几个这样的点；若不存在，请说明理由；‎ ‎（3）若在圆上存在点，使得直线与圆相交不同两点，求的取值范围.并求出使得的面积最大的点的坐标及对应的的面积. ‎ 数学（答案）‎ 一、选择题（每题5分，共60分）‎ ‎1、【答案】A【解析】,故选A.‎ ‎2、【答案】D【解析】设直线的倾斜率为，直线化为，故选D.‎ ‎3、【答案】A【解析】因为的斜率为，所以过点，且与直线垂直的直线的斜率为，因此过点，且与直线垂直的直线的方程为既是,故选A.‎ ‎4、【答案】D【解析】由于男生组与女生组有明显差异，所以适合分层抽样，选D.‎ ‎5、【答案】D【解析】①正确；②正确；③错误；④正确；‎ ‎6、【答案】C【解析】由已知可得圆心，半径，圆心直线距离，弦长为选C.‎ ‎7、【答案】D【解析】由题意得圆心在直线上，，故选D.‎ ‎8、【答案】B【解析】当;;‎ ‎,当时,输出，故应选B.‎ ‎9、【答案】A【解析】由图象，得；故选A． 10、【答案】C ‎11、【答案】D【解析】= ×（4+2+3+5）=3.5，= ×（49+26+39+54）=42，‎ ‎∴42=9.4×3.5+ ，解得=9.1.∴回归方程为=9.4x+9.1.当x=6时，=9.4×6+9.1=65.5‎ ‎12、【答案】B【解析】令，即，表示一条直线；又方程可化为，表示圆心为，半径的圆；由题意直线与圆有公共点，∴圆心到直线的距离 ‎ ，∴ ，即 的取值范围为.‎ 二、填空题（每题5分，共20分）‎ ‎13、【答案】【解析】将方程写成，‎ 对于任意值，等式成立，所以，；‎ 解得，所以A点的坐标是.故答案为：.‎ ‎14、【答案】【解析】由中点坐标公式得线段的中点坐标为，即圆心的坐标为； ，故所求圆的方程为：．故答案为：．‎ ‎15、【答案】【解析】，所以 ‎16、【答案】①②‎ 三、解答题（共70分）‎ ‎17、试题解析：解：（1）由分组内的频数是，频率是知，，‎ 所以．因为频数之和为，所以．‎ ‎．‎ 因为是对应分组的频率与组距的商，所以．‎ ‎（2）因为该校高二学生有人，分组内的频率是，‎ 所以估计该校高二学生参加社区服务的次数在此区间内的人数为人．‎ ‎18、试题解析：（1）∵样本中居民月用水量在3—3.5的频率 ‎∵样本中居民月用水量在3.5—4的频率 ‎∴样本中居民月用水量大于3的频率为（人）‎ 所以某小区2000户居民月用水量使用大于3的户数为 ‎ ‎（2）①众数是2.25. ‎ 利用频率分布直方图估计该样本的众数为2.25和中位数为2.019.‎ ‎19、试题解析：‎ 该试验所有可能的结果为：（1,1），（1,2），（1,3），（1,4），（1,5），（1,6），（2,1），（2,2），（2,3），（2,4），（2,5），（2,6），（3,1），（3,2），（3,3），（3,4），（3,5），（3,6），（4,1），（4,2），（4,3），（4,4），（4,5），（4,6），（5,1），（5,2），（5,3），（5,4），（5,5），（5,6），（6,1），（6,2），（6,3），（6,4），（6,5），（6,6），基本事件总数为36.‎ ‎（1）记事件A＝“点数之和是6”，则事件A，所含的基本事件为：（1,5），（2,4），（3,3），（4,2），（5,1）基本事件总数为4，所以P（A）＝.‎ ‎（2）记事件B＝“两数之积不是4的倍数”，则两数之积是4的倍数所含的基本事件为：（1,4），（2,2），（2,4），（2,6），（3,4），（4,1），（4,2），（4,3），（4,4），（4,5），（4,6），（5,4），（6,2），（6,4），（6,6），…，基本事件总数为15，所以P（B）＝.‎ ‎20、试题解析：（1）由调查数据可知，既未参加书法社团又未参加演讲社团的有人，故至少参加上述一个社团的共有人，所以从该班级随机选名同学，该同学至少参加上述一个社团的概率为 ‎（2）从这名男同学和名女同学中各随机选人，其一切可能的结果组成的基本事件，共个.‎ 根据题意，这些基本事件的出现是等可能的.‎ 事件“被选中且未被选中”所包含的基本事件有：，共个.‎ 因此被选中且未被选中的概率为.‎ ‎21、试题解析：（1）设直线方程为，将代入得，即所求直线方程是 ‎（2）若直线的斜率不存在，则过的直线为，到的距离为1，满足题意；‎ 若直线的斜率存在，设为，则的方程为.由到直线的距离为1，可得.解得.所以直线方程为.综上得所求的直线方程为或.‎ ‎22、试题解析：（1）设圆心是，它到直线的距离是，解得或（舍去）,所以,所求圆的方程是.（2）假设存在这样的点，则由，得 ‎.即，点P在圆D:上，点P也在圆C:上.因为，所以圆C与圆D外离，圆C与圆D没有公共点.所以，不存在点满足条件.‎ ‎（3）存在，理由如下：因为点在圆上，所以，且.因为原点到直线的距离，解得而，所以,‎ 因为，所以当，即时，取得最大值，‎ 此时点的坐标是或，的面积的最大值是.‎