2019届二轮复习正余弦函数图像及其性质学案(全国通用)
正余弦函数的图像
正余弦函数的值域和最值
正余弦函数的其他性质
一、正余弦函数的图像
(一)知识精讲
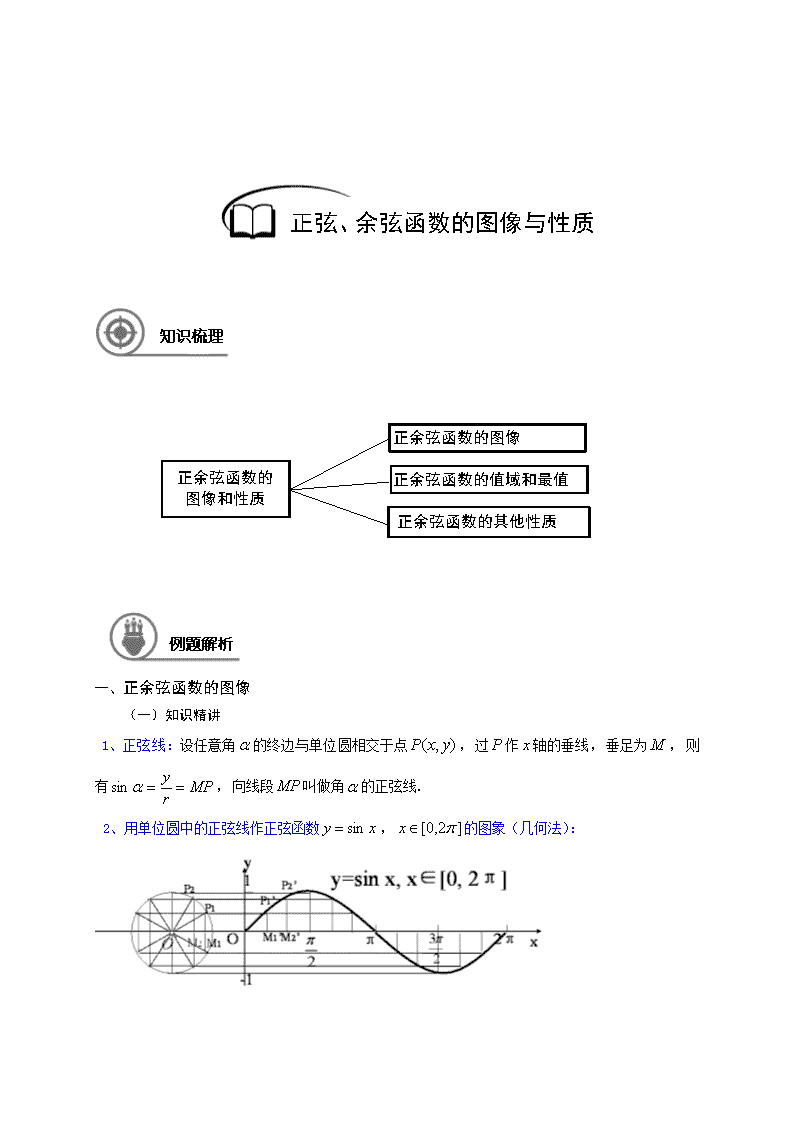
1、正弦线:设任意角 的终边与单位圆相交于点 ,过 作 轴的垂线,垂足为 ,则
有 ,向线段 叫做角 的正弦线.
2、用单位圆中的正弦线作正弦函数 , 的图象(几何法):
y=sin x, x∈[0, 2π]
M1
P1
M2
P2
M1’
P1’
M2’
P2’1
-1
π 2π x
y
O
2
π 3
2
π'O
α ),( yxP P x M
MPr
y ==αsin MP α
xy sin= ]2,0[ π∈x
正弦、余弦函数的图像与性质
知识梳理
正余弦函数的
图像和性质
例题解析
3、用五点法作正弦函数的简图(描点法):
正弦函数 , 的图象中,五个关键点是:
然后将这五点大致连线,画出正弦函数的图像。
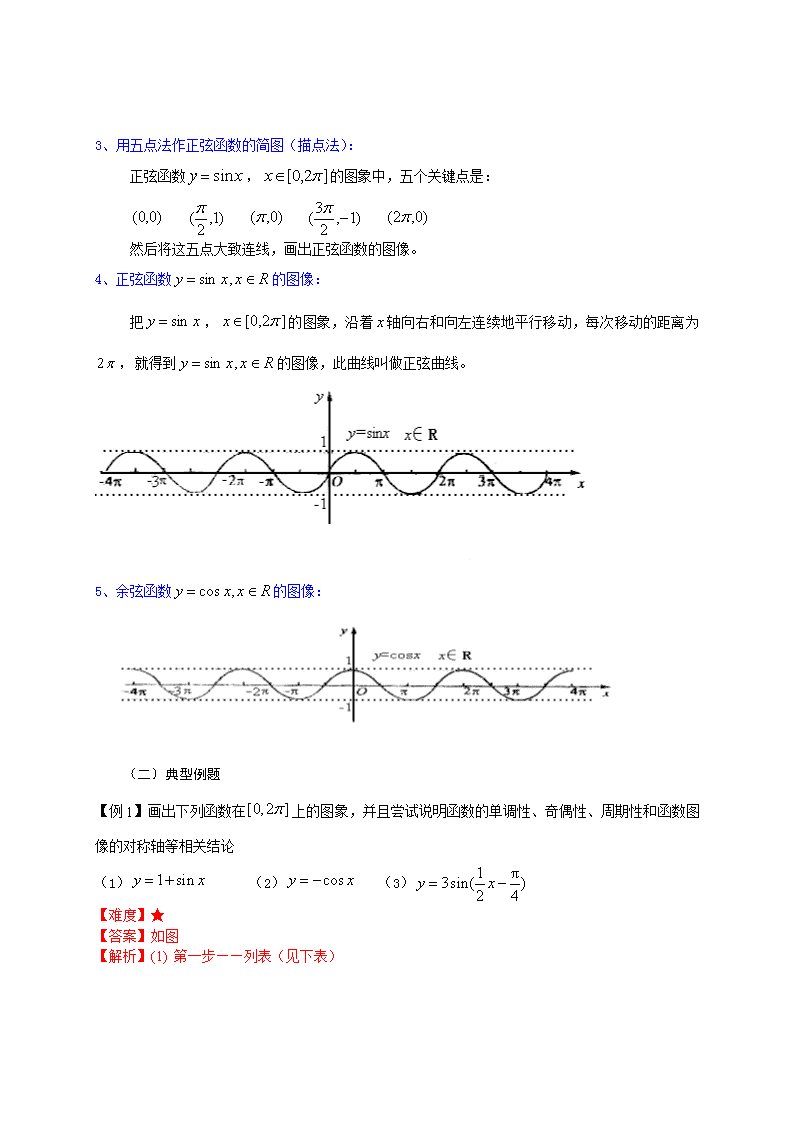
4、正弦函数 的图像:
把 , 的图象,沿着 轴向右和向左连续地平行移动,每次移动的距离为
,就得到 的图像,此曲线叫做正弦曲线。
5、余弦函数 的图像:
(二)典型例题
【例 1】画出下列函数在 上的图象,并且尝试说明函数的单调性、奇偶性、周期性和函数图
像的对称轴等相关结论
(1) (2) (3)
【难度】★
【答案】如图
【解析】(1) 第一步——列表(见下表)
xy sin= ]2,0[ π∈x
)0,0( )1,2(
π
)0,(π )1,2
3( −π
)0,2( π
Rxxy ∈= ,sin
xy sin= ]2,0[ π∈x x
π2 Rxxy ∈= ,sin
Rxxy ∈= ,cos
[0,2 ]π
1 siny x= + cosy x= − 1 π3sin( )2 4y x= −
第二步:描点、作图(见右上图)
(2) 第一步——列表(见下表)
第二步:描点、作图(见右上图)
(3)令 ,则
当 取 时,可相应取得 和 的值,得到“五点”,再描点作图.
【例 2】用五点作图法作函数 在 上的图象
【难度】★
【答案】如图
【解析】(1) 第一步——列表(见下表)
1
2 4X x
π= − 2( )4x X
π= +
X 30, , , ,22 2
π π π π x y
1 cosy x= − [0,2 ]π
第二步:描点、作图(见右上图)
【例 3】已知函数 的图像的一部分如下方左图,则下方右图的图像所对应的解析式为
( )
【难度】★
【答案】
【例 4】正弦函数的定义域是__________,最大值是____,最小值是____,周期是____,
递增区间是_____________________,递减区间是______________________.
对称轴是______________,对称中心是_____________;
【难度】★
【答案】定义域是 ,最大值 1,最小值-1,周期 ,单调增区间
单调减区间
,
对称轴方程: 对称中心:
【例 5】定义函数 ,根据函数的图像与性质填空:
(1) 该函数的值域为_______________;(2) 当且仅当________________时,该函数取得最大值;
xxf πsin)( =
.A )2
12( −= xfy .B )12( −= xfy .C )12( −= xfy .D )2
1
2( −= xfy
B
x R∈ 2π 2 ,22 2k k
π ππ π − +
32 ,2 ( )2 2k k k Z
π ππ π + + ∈ 2x k
ππ= + ( ),0kπ
sin , sin cos( ) cos , sin cos
x x xf x x x x
≤= >
-1
y
x
0 1
1
-1
y
x -1
1
0 0.5 1
-1
(3) 该函数是以________为最小正周期的周期函数;(4) 当且仅当______________时, .
【难度】★★
【答案】(1) ;(2) ; (3) ; (4)
【例 6】求函数 y=-cosx 的单调区间
【难度】★★
【答案】单调增区间为
单调减区间为
【例 7】求下列函数的定义域与值域
(1) (2)
【难度】★★
【答案】定义域为 R,值域是
定义域为 ,值域为 .
【解析】(1)∵ 的定义域为 ,值域是 ;∴ 的定义域应是 ,即
,值域是 ;
(2)虽然 的定义域为 ,值域是 .但本题中 作为二次根式的被开方数,
所以 ,即 .根据余弦比的符号可求得 求值范围,并由 ,可得
函数值域.
【巩固训练】
1、已知函数 ,用“五点法”作出它在一个周期内的图像;
【难度】★
【答案】令 ,则 。列表并描点作图,
得
( ) 0f x >
2[ 1, ]2
− 2 ,4x k k Z
ππ= + ∈ 2π 2 2 ( )2k x k k Z
ππ π< < + ∈
[ ]2 ,2 ( )k k k Zπ π π+ ∈
[ ]2 ,2 ( )k k k Zπ π π− ∈
xy 2sin2
1= xy cos2−=
2
1
2
1- ,
)(,2
3222 zkkxk ∈+≤≤+ ππππ 0, 2
siny x= R [ 1,1]− 1 sin 22y x= 2x R∈
x R∈ 1 1[ , ]2 2
−
cosy x= R [ 1,1]− 2cos x−
2cos 0x− ≥ cos 0x ≤ x 0 2cos 2x≤ − ≤
π2sin(2 )3y x= +
π2 3X x= + π2sin(2 ) 2sin3y x X= + =
2、已知函数 ,用五点法作出函数的图像;
【难度】★
【答案】列表描点作图
3、函数 的部分图像是( )
【难度】★
【答案】
4、余弦函数的定义域是______,最大值是______,最小值是____,周期是____,
递增区间是_____________________,递减区间是______________________.
对称轴是__________________,对称中心是____________;
【难度】★
A
o
y
x
B
o
y
x
C
o
y
x
D
o
y
x
1 π3sin( )2 4y x= −
cosy x x= − ⋅
D
【答案】定义域是 ,最大值 1,最小值-1,周期 ,递增区间是单调增区间为
,递减区间是 ;对称轴 ,对
称中心 .
5、判断函数 的奇偶性和单调性,并写出的单调区间.
【难度】★★
【答案】 ,为偶函数,单调递增区间为 ,单调递减
区间为 .
6、设 和 分别表示函数 的最大值和最小值,则 等于( )
A. B.- C.- D.-2
【难度】★★
【答案】D
二、正余弦函数的值域与最值
(一)知识精讲
1、正、余弦函数定义域: 和 的定义域都为 R。
2、正、余弦函数定义域: 和 的值域都为 。
对于函数 ,当且仅当 取最大值 ;
当且仅当 取最小值 。
对于函数 ,当且仅当 取最大值 ;
当且仅当 取最小值 。
x R∈ 2π
[ ]2 ,2 ( )k k k Zπ π π− ∈ [ ]2 ,2 ( )k k k Zπ π π+ ∈ ,x k k Zπ= ∈
Zkk ∈+ )0,2(
ππ
sin( )2y x
π= −
sin( )= cos2y x x
π= − − [ ]2 ,2 ( )k k k Zπ π π+ ∈
[ ]2 ,2 ( )k k k Zπ π π− ∈
M m 1cos3
1 −= xy M m+
3
2
3
2
3
4
xy sin= cosy x=
xy sin= cosy x= [ ]1,1−
xy sin= ,22
ππ += kx y 1max =y
2 ,2x k
ππ= − y 1min −=y
cosy x= ,2 πkx = y 1max =y
,2 ππ += kx y 1min −=y
(二)典型例题
【例 8】要使下列各式有意义应满足什么条件?
(1) (2)
【难度】★
【答案】(1)由
当 时,式子有意义.
(2)由
即
当 时,式子有意义.
【例 9】求下列函数的最大值,以及取得最大值时的 x 值
(1) y=sinx+cosx (2)y=asinx+b
【难度】★★
【答案】(1)(分析:这个函数不是 sinx 或 cosx 型函数,而是 asinx+bcosx 型)
∴y=sinx+cosx= sin( )≤ ,当 时取“=”,
即当 x=2kπ 时,ymax=
(2)显然|sinx|≤1,∴|asinx|≤|a| 即 asinx≤|a|
∴asinx+b≤|a|+b;
当 a>0 时,asinx+b≤a+b 当 sinx=1 即 x=2kπ+ 时取“=”
∴此时,当 x=2kπ+ 时,ymax=a+b
当 a<0 时,∴当 x=2kπ+ 时,ymax=-a+b (以上 K∈Z)
【例 10】求使下列函数取得最大值的自变量 x 的集合,并说出最大值是什么.
(1) y=sin(3x+ )-1 (2)y=sin2x-4sinx+5 (3) y=
【难度】★★
1sin ;2
mx m
−= −
2 2
cos 2
a bx ab
+=
2 21 3| sin | 1 | | 1 (1 ) (2 ) .2 2
mx m m mm
−≤ ⇒ ≤ ⇒ − ≤ − ⇒ ≤−
∴ 3
2m ≤
2 2
2 2 2 2| cos | 1 | | 1 ( ) (2 )2
a bx a b abab
+≤ ⇒ ≤ ⇒ + ≤
2 2 2 2 2( ) 0 ,a b a b⇒ − ≤ ⇒ = .a b= ±
∴ a b= ±
2 4
π+x 2 224
πππ +=+ kx
4
π+ 2
2
π
2
π
2
3π
4
π
x
x
cos3
cos3
+
−
【答案】(1) x= (k∈Z)时 ymax=0
(2)当 x=2kπ- k∈Z 时 ymax=10
(3) 当 x=2kπ+π k∈Z 时 ymax=2
【例 11】求下列函数的值域
(1) (2) (3)
【难度】★★
【答案】(1) (2) (3)
【解析】解:(1) ,由 ,
故 , 。
(2) ,
令 ,由 , ,则 ,
当 ,即 时, . 当 ,即 时, .
所以 .
(3) ,由 得
解得 所以函数 的值域是
123
2 ππ +k
2
π
sin 3 cos , ,6 2y x x x
π π = − ∈ −
2cos sin , ,4 4y x x x
π π = + ∈ −
1 cos
3 cos
xy x
−= +
[ )2,1y ∈ − 1 2 5,2 4y
−∈
( , 3] [1, )−∞ − ∞
sin 3 cos =2sin( )3y x x x
π= − − ,6 2x
π π ∈ − ,3 2 6x
π π π − ∈ −
1sin( ) [ 1, )3 2x
π− ∈ − [ )2,1y ∈ −
2 2cos sin sin sin 1y x x x x= + = − + +
sin x t= ,4 4x
π π ∈ −
2 2,2 2t
∈ −
2 21 51 ( )2 4y t t t= − + + = − − +
1
2t =
6x
π= max
5
4f = 2
2t =
4x
π= − min
1 2
2f
−=
1 2 5,2 4y
−∈
1 cos
3 cos
xy x
−= + ⇒ (1 )cos 1 3y x y+ = − ⇒ 1 3cos 1
yx y
−= + | cos | 1x ≤ 1 3 11
y
y
− ≤+
[ ]0,1y∈ 1 cos
3 cos
xy x
−= + [ ]0,1
【例 12】已知函数 , ,求 的最大值和最小值.
【难度】★★
【答案】 .
因为 ,所以 .
当 ,即 时, 的最大值为 ;
当 ,即 时, 的最小值为 。
【巩固训练】
7、求使下列函数取得最大值的自变量 x 的集合,并说出最大值是什么
(1)y=cosx+1,x∈R;
(2)y=sin2x,x∈R。
【难度】★★
【答案】 (1)函数 y=cosx+1,x∈R 的最大值是 1+1=2 此时
(2)函数 y=sin2x,x∈R 的最大值是 1。此时
8、函数 y=ksinx+b 的最大值为 2, 最小值为-4,求 k,b 的值。
【难度】★★
【答案】当 k>0 时
当 k<0 时 (矛盾舍去)
9、函数 的最大值为 .
【难度】★
【答案】9
【解析】
又 ,结合函数解析式,当且仅当 时,
( ) 23sin sin cosf x x x x= + ⋅ ,2x
π π ∈
( )f x
3 1 π 3( ) 1 cos2 sin 2 sin(2 )2 2 3 2f x x x x= − + = − +( )
π[ ,π]2x∈ π 2π 5π2 [ ]3 3 3x − ∈ ,
π 2π2 3 3x − = π
2x = ( )f x 3
π 3π2 3 2x − = 11π
12x = ( )f x 31 2
− +
2 ,x k k Zπ= ∈
,4x k k Z
π π= + ∈
−=
=⇒
−=+−
=+
1
3
4
2
b
k
bk
bk
−=
=⇒
−=+
=+−
1
3
4
2
b
k
bk
bk
3cos6sin2)( 2 ++= xxxf
2 2 23 19( ) 2sin 6cos 3 2cos 6cos 5 2(cos )2 2f x x x x x x= + + = − + + = − − +
1 cos 1x− ≤ ≤ cos 1x = max 9y =
10、函数 的值域为 .
【难度】★★
【答案】
【解析】
又
11、函数 的最大值为_________.
【难度】★★
【答案】
【解析】
,由三角函数有界性得
12、已知 求 的最大值及此时 的集合.
【难度】★★
【答案】最大值为 ,此时 的集合为 .
【解析】解:
∵ ,
∴当 时, .此时, 即 .
所以 的最大值为 ,此时 的集合为 .
])2,0[(2cos2sin
π∈+= xxxy
[ 1, 2]−
sin 2 cos2 2 sin(2 )4y x x x
π= + = +
20 , sin(2 ) 12 2 4x x
π π≤ ≤ ∴− ≤ + ≤ 1 2y∴− ≤ ≤
−
+= xxy 6cos2sin
ππ
2 3
4
+
23 1 3 1sin( )cos( ) cos ( s sin ) cos sin 22 6 2 2 2 4y x x x co x x x x
π π= + − = ⋅ + = +
3 1 3 1 3cos2 sin 2 cos(2 )4 4 4 2 6 4x x x
π= + + = − + maxy = 2 3
4
+
Rxxxxy ∈+⋅+= ,1cossin2
3sin2
1 2 y x
7
4 x { | , }6x x k k Z
ππ= + ∈
21 3sin sin cos 12 2y x x x= + ⋅ + 1 cos2 3 1 5sin 2 1 sin(2 )4 4 2 6 4
x x x
π+= + + = + +
sin(2 ) 16x
π+ =
max
1 5 7
2 4 4y = + = 2 2 ,6 2x k
π ππ+ = +
6x k
ππ= +
y 7
4 x { | , }6x x k k Z
ππ= + ∈
三、正余弦函数的其他性质
(一)知识精讲
正余弦函数的性质与图像
函数
定义域
值域
有界性 有界函数 有界函数
奇偶性 奇函数 偶函数
对称性
对称轴方程:
对称中心:
对称轴方程:
对称中心:
周期性 周期函数 周期函数
单调性
单调增区间
单调减区间
单调增区间
单调减区间
1
-1
y=sinx
-3π
2
-5π
2
-7π
2
7π
2
5π
2
3π
2
π
2
-
π
2
-4π -3π -2π 4π3π2ππ-π o
y
x
1
-1
y=cosx
-3π
2
-5π
2
-7π
2
7π
2
5π
2
3π
2
π
2
-
π
2
-4π
-3π
-2π 4π
3π
2π
π-π
o
y
x
siny x= cosy x=
R R
[ ]1,1− [ ]1,1−
sin 1x ≤ cos 1x ≤
2x k
ππ= +
( ),0kπ
x kπ=
,02k
ππ +
( 2 )T π= ( 2 )T π=
2 ,22 2k k
π ππ π − +
32 ,2 ( )2 2k k k Z
π ππ π + + ∈
[ ]2 ,2k kπ π π−
[ ]2 ,2 ( )k k k Zπ π π+ ∈
最值性
周期函数:一般地,对于函数 ,如果存在一个非零常数 ,使得当 取定义域内的每一个
值时,都有 ,那么函数 就叫做周期函数,非零常数 叫做这个函数的周期
由此可知 都是这两个函数的周期
对于一个周期函数 ,如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫
做 的最小正周期
根据上述定义,可知:正弦函数、余弦函数都是周期函数, 都是它的周期,
最小正周期是
注意:
1.周期函数定义域 ,则必有 ,且若 ,则定义域无上界; 则定义域
无下界;
2.“每一个值”只要有一个反例,则 就不为周期函数;
3. 往往是多值的(如 中 都是周期)周期 中最小的正数叫
做 的最小正周期(有些周期函数没有最小正周期)
(二)典型例题
【例 13】利用正弦函数和余弦函数的图像,求满足下列条件的 的集合:
【难度】★★
【 答 案 】 ( 1 ) ; ( 2 )
max
min
2 ,( ), 12
2 ,( ), 12
x k k Z y
x k k Z y
ππ
ππ
= + ∈ =
= − ∈ = −
max
min
2 ,( ), 1
2 ,( ), 1
x k k Z y
x k k Z y
π
π π
= ∈ =
= + ∈ = −
)(xf T x
)()( xfTxf =+ )(xf T
)0(2,,4,2,2,4, ≠∈−− kzkk 且πππππ
)(xf
)(xf
)0(2 ≠∈ kzkk 且π
π2
Mx∈ MTx ∈+ 0>T 0
0)
(4)y=|sinx|+|cosx|
【难度】★★
【答案】(1)∵ ,故只有当自变量 x 增加到 x+4π,且必须增加到 x+4π 时,
函数 的值才重复出现。
∴ 的周期为 4π。
sin , [0,2 ]y x x π= ∈
x 52 , 2 ,6 6k k k Z
π ππ π + + ∈
cos , [0,2 ]y x x π= ∈
x 52 , 2 ,3 3k k k Z
π ππ π + + ∈
)25lg(2sin 2xxy −+=
2
1sin
16
y x
x
= +
−
1lg[cos( ) ]3 2y x
π= − +
3 3( 5, ] [ , ] [0, ] [ , ]2 2 2 2
π ππ π π π− − ∪ − − ∪ ∪ ( 4, ] [0, ]x π π∈ − −
(2 ,2 )3x k k
ππ π π∴ ∈ − +
2
sin 2 0
25 0
x
x
≥
− > 2
5 5
k x k
x
ππ π ≤ ≤ +
− < <
3 3( 5, ] [ , ] [0, ] [ , ]2 2 2 2
π ππ π π π− − ∪ − − ∪ ∪
sin 0x ≥ 2 16x < ( 4, ] [0, ]x π π∈ − −
1cos( )3 2x
π− > − (2 ,2 )3x k k
ππ π π∴ ∈ − +
2sin xy = xxy cos3sin −= ϕ
)]4(2
1sin[)22sin( ππ +=+ xx
2sin x
2sin xy =
(2)∴ , ∵
∴ 的周期为 2π
(3)∵sin(ωx+ +2π)=
∴ 的周期为
(4)∴
∴函数 的周期即函数 cos4x 的周期
∵
∴函数 的周期为 。
【例 16】判断下列函数的奇偶性
(1) (2)
【难度】★
【答案】(1)非奇非偶 (2)既是奇函数又是偶函数
【例 17】求列函数的单调增区间
( 1 ) ( 2 ) ( 3 )
( 4 )
.
【难度】★★
【答案】 (1) (2)
(3) ( ) (4) ( )
【例 18】(1)函数 的对称轴方程是
)3sin(2cos3sin
π−=−= xxxy ]3)2sin[()23sin(
ππππ −+=+− xx
xxy cos3sin −=
ϕ ])2(sin[ ϕω
πω ++x
)sin( ϕω += xAy ω
π2
|2sin|1|cossin|21|)cos||sin(||cos||sin| 2 xxxxxxxy +=+=+=+=
2
4cos11 x−+=
|cos||sin| xxy +=
)]2(4cos[)24cos(
ππ +=+ xx
|cos||sin| xxy +=
2
π
1 sin cos( ) 1 sin cos
x xf x x x
+ −= + +
4 4( ) sin cos cos2f x x x x= − +
cos2y x= 2sin( )4y x
π= − 1 2sin( )2 4 3
xy
π= −
π| sin( ) |4y x= − +
[ , ],2k k k Z
ππ π− ∈ 3 7[2 ,2 ],4 4k k k Z
π ππ π+ + ∈
9 21π[3 ,3 ]8 8k k
ππ π+ + k Z∈ 3π[ , ]4 4k k
ππ π+ + k Z∈
3sin(2 )3y x
π= +
(2)若函数 的图像关于 对称,则
【难度】★
【答案】(1) , (2)
【例 19】求函数 的单调递增区间.
【难度】★★
【答案】∵ 令 ∴
是 的增函数 又 ∵
∴ 当 为单调递增时 为单调递减 且
∴
∴ ,
∴ 的单调递减区间是
【例 20】已知函数 .
(1)求函数 的最小正周期,最大值及取最大值时相应的 值;
(2)如果 ,求 的取值范围.
【难度】★★
【答案】(1) ; 当 , 时, 取得最大值 2.
(2)
【解析】(1)
sin 2 cos2y x a x= +
3x
π= a =
1
2 12x k
ππ= + k Z∈ 3
3a = −
1
2
1( ) log cos( )3 4f x x
π= +
1
2
1( ) log cos( )3 4f x x
π= + 1
3 4t x
π= + 1
2
log cosy t=
t x 10 12
< <
1
2
log cosy t= cost cos 0t >
2 2 ( )2k t k k Z
ππ π≤ < + ∈
2 2 ( )3 4 2
xk k k Z
π ππ π≤ + < + ∈ 3 36 6 ( )4 4k x k k Z
π ππ π− ≤ < + ∈
1
2
1( ) log cos( )3 4f x x
π= + 3 36 6 ( )4 4k x k k Z
π ππ π− ≤ < + ∈
xxxxxxf 2coscossin3)3sin(sin2)( +⋅+−⋅= π
)(xf x
20
π≤≤ x )(xf
π 2 26 2x k
π ππ+ = +
6x k
ππ= + ( )k z∈ ( )f x
[ 1, 2]−
2 2 23 1( ) 2sin ( cos sin ) 3sin cos cos 2 3sin cos cos sin2 2f x x x x x x x x x x x= − + + = + −
,所以 的最小正周期等于 .
当 , 时, 取得最大值 2.
(2)由 ,得 , ,
的值域为
【例 21】设
(1)求当 时,函数图象的对称轴方程和对称中心坐标.
(2)求最小正整数 ,使得当自变量在任意两个整数间(包括整数本身)变化时,函数至少取得一
次最大值 和最小值 .
【难度】★★
【答案】(1) , (2)
【例 22】(1) 取何值时,方程 无解?有一解?有两
解?有三解?
(2)函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究
顺序,研究函数 的性质.
【难度】★★
【答案】见解析
【解析】(1) 或 时无解; 时一解; 或 时有两
解 ; 时 三 解 ; ( 2 ) 定 义 域 为 ; 值 域 为 ; 周 期 为 ; 偶 函 数 ; 增 区 间 :
;减区间: .
【巩固训练】
13、在下列四个函数中,周期为 的偶函数为 ( )
. .
3sin 2 cos2 2sin(2 )6x x x
π= + = + ( )f x π
2 26 2x k
π ππ+ = +
6x k
ππ= + ( )k z∈ ( )f x
0 2x
π≤ ≤ 726 6 6x
π π π≤ + ≤ 1 sin(2 ) 12 6x
π− ≤ + ≤
( )f x [ 1, 2]−
( ) sin ( 0)5 3
kf x x k
π = + ≠
3k =
k
M m
5 5 ,3 18
kx k Z
π π= + ∈ 5 5( ,0),3 9
k k Z
π π− ∈ 32k =
a [ ]( )2 2sin 2sin cos cos 0,x x x x a x π+ − = ∈
( ) 1 sin 1 sinf x x x= − + +
2a > 2a < − 2a = ± 2 1a− < < − 1 2a− < <
1a = − R 2,2 π
,2k k
ππ π π + + , ,2k k k Z
ππ π + ∈
2
π
A 2sin 2 cos2y x x= B 2 2cos 2 sin 2y x x= −
. .
【难度】★
【答案】B
14、(1)函数 的图像关于 轴对称,则 = _______________
(2)函数 为奇函数,则
【难度】★★
【答案】(1) .(2)
15、函数 图像的一条离直线 最近的对称轴方程是 .
【难度】★★
【答案】
【解析】由 得: , 故而离直线 最近的对称
轴方程是
16、函数 的单调递增区间__________
【难度】★★
【答案】
【解析】 ,由 得:
,在数轴上与 取交集得:函数在 上单调递增。
17、已知函数 .
求:(I)函数 的最小正周期;(II)函数 的单调增区间.
【难度】★★
C sin 2y x x= D 2 2cos siny x x= −
sin(2 )y x ϕ= + y ϕ
5cos(2 )y x θ= − θ =
,2k k Z
πϕ π= + ∈ ,2k k Z
πθ π= + ∈
3sin 2 6y x
π = + 10x =
19
6x
π=
2 ( )6 2x k k Z
π π π+ = + ∈ ( )6 2
kx k Z
π π= + ∈ 10x =
19
6x
π=
∈+=
2,0,cos3sin
π
xxxy
0, 6
π
sin 3 cos 2sin( )3y x x x
π= + = + 2 2 ( )2 3 2k x k k Z
π π ππ π− + ≤ + ≤ + ∈
5 2 2 ( )6 6k x k k Z
π ππ π− + ≤ ≤ + ∈ 0, 2
π
0, 6
π
2 π π π( ) 1 2sin 2sin cos8 8 8f x x x x = − + + + +
( )f x ( )f x
【答案】(1) (2) ( ).
【解析】 .
(I)函数 的最小正周期是 ;
(II)当 ,即 ( )时,函数 是增函数,故函
数 的单调递增区间是 ( ).
18、已知函数 (1)求 的最小正周期及 取得最大值
时 的集合;(2)求证:函数 的图像关于直线 对称.
【难度】★★
【答案】见解析
【 解 析 】 ( 1 ) ; ; ( 2 ) 提 示 : 证 明
.
19、已知函数 , .
(1)请指出函数 的奇偶性,并给予证明;
(2)当 时,求 的取值范围.
【难度】★★
【答案】(1)非奇非偶函数.(2)
【解析】
(1) ,
πT = π[ π , π]2k k− k Z∈
π π( ) cos(2 ) sin(2 )4 4f x x x= + + + π π π2 sin(2 ) 2 sin(2 ) 2 cos24 4 2x x x= + + = + =
( )f x 2π π2T = =
2 π π 2 2 πk x k− ≤ ≤ ππ π2k x k− ≤ ≤ k Z∈ ( ) 2 cos2f x x=
( )f x π[ π , π]2k k− k Z∈
( ) 24sin 2sin 2 2,f x x x x R= + − ∈ ( )f x ( )f x
x ( )f x 8x
π= −
T = π 3| ,8x x k k Z
ππ = + ∈
8 8f x f x
π π − − = − +
)cos(sincos)( xxxxf += R∈x
)(xf
∈
2,0
π
x )(xf
2 1( ) 0, 2f x
+∈
2 1( ) sin 22 4 2f x x
π = + +
1 2 1
8 2 2 8f f
π π+ − = ≠ ± = ±
是非奇非偶函数.
(2)由 ,得 , .
所以 .即 .
熟练掌握正弦函数、余弦函数、正切函数的性质及图形特点:
三角函数
定义域
值域
奇偶性 奇函数 偶函数
周期性
单调性
在 上递增
在 上递减
在 上递增
在 上递减
最值
时,最大值 1
时,最小值
时,最大值 1
时,最小值
图像
( )f x∴
0, 2x
π ∈
524 4 4x
π π π≤ + ≤ 2 sin 2 12 4x
π − ≤ + ≤
2 1 2 10 sin 22 4 2 2x
π + ≤ + + ≤
2 1( ) 0, 2f x
+∈
siny x= cosy x=
R R
[ 1,1]− [ 1,1]−
2π 2π
2 22 2k k
π ππ π − + ,
32 22 2k k
π ππ π + + ,
[ ]2 2k kπ π π− ,
[ ]2 2k kπ π π+,
2 2x k
ππ= +
2 2x k
ππ= − 1−
2x kπ=
2x kπ π= + 1−
反思总结
1、已知函数 ,
⑴讨论函数 的奇偶性 ⑵求当 取最大值时,自变量 的取值集合.
【难度】★★
【答案】见解析
【解析】(1)若 ,则函数是偶函数,若 则函数既不是奇函数也不是偶函数
(2)若 ,则函数的最大值为 ,此时
若 ,则函数的最大值为 ,此时
2、、已知 是实数,则函数 的图像不可能是 ( )
【难度】★★
【答案】D
3、函数 的最大值为 .
【难度】★★
【答案】
【解析】
当且仅当 时,
4、求函数 的值域.
【难度】★★
【答案】
【解析】解:
( ) sinf x x a= − a R∈
( )f x ( )f x x
0a = 0a ≠
0a ≥ |1 |a+ 2 ,2x k k Z
ππ= − ∈
0a < |1 |a− 2 ,2x k k Z
ππ= + ∈
a ( ) 1 sinf x a ax= +
2sin 2 2cosy x x= −
2 1−
2sin 2 2cos sin 2 cos2 1 2 sin(2 ) 14y x x x x x
π= − = − − = − −
sin(2 ) 14x
π− = max 2 1y = −
]3,6[,sin2cos87 2 ππ−∈−−= xxxy
3[ 1, ]2y∈ −
课后练习
∵ = ∵ ,
∴ ,∴ .
5、求函数 的最小值.
【难度】★★
【答案】
【解析】解:设 则 ,
所以 = ,当 时, 有最小值 .
6、函数 的单调递增区间为 .
【难度】★★
【答案】
7、函数 的最小正周期是__________.
【难度】★★
【答案】
8、已知函数 .
(Ⅰ)求函数 的最小正周期;
(Ⅱ)求函数 在区间 上的最小值和最大值.
【难度】★★
【答案】(1) 的最小正周期为 (2) 最大值为 ,最小值为 .
【解析】解:(Ⅰ) .
因此,函数 的最小正周期为 .
27 8cos 2siny x x= − − 2 27 8cos 2(1 cos ) 2(cos 2) 3x x x− − − = − − [ , ]6 3x
π π∈ −
1cos [ ,1]2x∈ 3[ 1, ]2y∈ −
sin cos sin cosy x x x x= + +
1−
sin cos ,x x t+ = [ 2, 2],t ∈ −
2 1sin cos 2x x t −=
( )y f t= 21 1,2 ( 1)t⋅ −+ ( [ 2, 2])t ∈ − 1 [ 2, 2]t = − ∈ − y 1−
)cos(sin xxy −−= π )R( ∈x
Zkkk ∈+− ],42,4
32[
ππππ
1 cotsiny xx
= −
π2
( ) 2cos (sin cos ) 1f x x x x x= − + ∈R,
( )f x
( )f x π 3π
8 4
,
( )f x π ( )f x 2 1−
π( ) 2cos (sin cos ) 1 sin 2 cos2 2 sin 2 4f x x x x x x x = − + = − = −
( )f x π
(Ⅱ)解法一:因为 在区间 上为增函数,在区间 上为减
函数,又 , , ,
故函数 在区间 上的最大值为 ,最小值为 .
解法二:作函数 在长度为一
个周期的区间 上的图象如下:由图象得函数
在 区 间 上 的 最 大 值 为 , 最 小 值 为
.
9、已知函数 , .
(1)设 是函数 图象的一条对称轴,求 的值.(2)求函数
的单调递增区间.
【难度】★★
【答案】见解析
【解析】(1)由题设知 .因为 是函数 图象的一条对称轴,所以
,即 ( ).所以 .当 为偶
数时, ,当 为奇数时, .
(2)
.
π( ) 2 sin 2 4f x x = −
π 3π,8 8
3π 3π,8 4
π 08f =
3π 28f =
3π 3π π π2 sin 2 cos 14 2 4 4f = − = − = −
( )f x π 3π,8 4
2 1−
π( ) 2 sin 2 4f x x = −
π 9π,8 4
( )f x π 3π,8 4
2
3π 14f = −
2 π( ) cos 12f x x = +
1( ) 1 sin 22g x x= +
0x x= ( )y f x= 0( )g x ( ) ( ) ( )h x f x g x= +
1 π( ) [1 cos(2 )]2 6f x x= + + 0x x= ( )y f x=
0
π2 6x + πk= 0
π2 π 6x k= − k Z∈ 0 0
1 1 π( ) 1 sin 2 1 sin( π )2 2 6g x x k= + = + − k
0
1 π 1 3( ) 1 sin 12 6 4 4g x = + − = − = k 0
1 π 1 5( ) 1 sin 12 6 4 4g x = + = + =
1 π 1( ) ( ) ( ) 1 cos 2 1 sin 22 6 2h x f x g x x x
= + = + + + +
1 π 3 1 3 1 3cos 2 sin 2 cos2 sin 22 6 2 2 2 2 2x x x x
= + + + = + +
1 π 3sin 22 3 2x = + +
y
xO
2
2−
π
8
3π
8
5π
8
3π
4 7π
8
9π
8
当 ,即 ( )时,
函 数 是 增 函 数 , 故 函 数 的 单 调 递 增 区 间 是
( ).
10、若函数 f(x)=cos2x-asinx+b 的最大值为 0,最小值为-4,且 a>0,求 a,b 的值
【难度】★★
【答案】解:∴f(x)=1-sin2x-asinx+b=-(sinx+ )2+ +b+1
∵a>0 ∴ >0
①若 时,当 sinx=-1 时,fmax=a+b
当 sinx=+1 时,fmin=b-a
由题意 ∴a=2 不满足
②若 0< ≤1 时,当 时,
当 sinx=1 时,fmin=a+b
∴ ∴ ∴a2+4a-12=0
∴a=2(满足 )∴b=-2
综上满足条件的 a=2;b=-2
π π π2 π 2 2 π2 3 2k x k− ≤ + ≤ + 5π ππ π12 12k x k− ≤ ≤ + k Z∈
1 π 3( ) sin 22 3 2h x x = + + ( )h x 5π ππ , π12 12k k − +
k Z∈
2
a 2
4
a
2
a
12
>a
−=+−
=+
4
0
ba
ba 12
>a
2
a
2sin ax −= 14
2
max ++= baf
−=+−
=++
4
014
2
ba
ba
34
2
=+ aa
12
=a