高中数学选修2-2教学课件2_3数学归纳法1

高中数学选修2-2教学课件2_3数学归纳法1

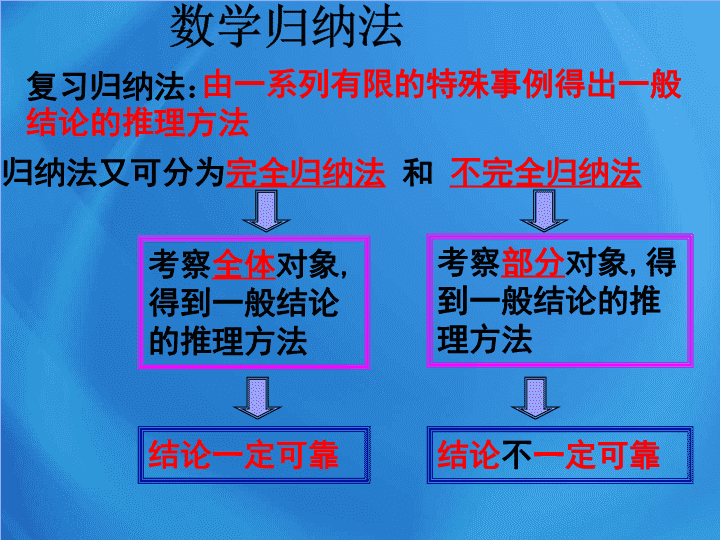
复习归纳法 ： 结论一定可靠 结论 不 一定可靠 考察 全体 对象 , 得到一般结论的推理方法 考察 部分 对象 , 得到一般结论的推理方法 归纳法又可分为 完全归纳法 和 不完全归纳法 由一系列有限的特殊事例得出一般结论的推理方法 可从简单情形出发 观察、归纳、猜想 ( 不完全归纳法 ) 费马 (Fermat) 曾经提出一个猜想： 形如 F n ＝ 2 2 n +1( n =0,1,2 … ) 的数都是质数 …… 100 年后 … 费马 (1601--1665) 法国伟大的业余数学家。 欧拉 (1707 ～ 1783) ，瑞士数学家及自然科学家。 费马您错了 ! 不完全归纳法能帮助我们发现猜想 , 但不能保证猜想正确 . 其中道理可用于数学证明 ──数学归纳法 . 播放视频 1 播放视频 2 这种一种严格的证明方法 ── 数学归纳法 . 1. 验证第一个命题成立 ( 即 n ＝ n 0 第一个命题对应的 n 的值，如 n 0 ＝ 1) ； 2. 假设当 n = k 时命题成立，证明当 n = k ＋ 1 时命题也成立 . ( 归纳奠基） 数学归纳法 : 关于正整数 n 的命题 ( 相当于多米诺骨牌 ), 我们可以采用下面方法来证明其正确性： 由 (1) 、 (2) 知，对于一切 n ≥ n 0 的自然数 n 都成立！ ( 归纳递推） 注意 : 运用数学归纳法证题 , 以上两步缺一不可 . 验证 n=n 0 时命题成立 若 当 n=k( kn 0 ) 时命题成立 , 证明当 n=k+1 时命题也成立 命题对从 n 0 开始的所有正整数 n 都成立． 思考 1 ：下面的推理是否正确 ? 错在没有奠基等式 思考 2 ：下面用数学归纳法证明的过程是否正确 : 错在第二步证明没有用上假设 用上假设 , 递推才成立 数学归纳法具体应用： 例 1. 用数学归纳法证明： 第二步证明是关键 : 1. 要用到归纳假设作为理由 . 2. 看清从 k 到 k ＋ 1 中间的变化 . 例 2 ( 课本第 84 页 B 组第 1 题 ) 已知数列 { a n } 中 , a 1 = , 其前 n 项和 S n 满足： ( n ≥ 2), 计算 S 1 , S 2 , S 3 , S 4 , 猜想 S n , 并证明 . 1+3+5 + …… +(2 n -1 )= n 2 ( n ∈ N ） .  例 1: 用数学归纳法证明 1+3+5 + …… +(2 n -1 )= n 2 ( n ∈ N ） .  证明 : ( 1) 当 n =1 时 , 左＝ 1 ，右＝ 1 2 ＝ 1 ∴ n =1 时，等式成立 (2) 假设 n = k 时，等式成立，即 1+3+5+…+(2 k  1)= k 2 那么，当 n = k +1 时 左＝ 1+3+5+…+(2 k  1) ＋ [2( k +1)-1] = k 2 +2 k +1 =( k +1) 2 = 右 即 n = k +1 时等式成立 由 (1) 、 (2) 可知等式对任何 n N * 都成立 递推基础 递推依据 例 2 ( 课本第 84 页 B 组第 1 题 ) 已知数列 { a n } 中 , a 1 = , 其前 n 项和 S n 满足： ( n ≥ 2), 计算 S 1 , S 2 , S 3 , S 4 , 猜想 S n , 并证明 . 当 n = k +1 时： a k +1 = S k +1 - S k = S k +1 + +2    解： S 1 = a 1 = , S 2 = , S 3 = , S 4 = . 猜想 S n = . 证明： 1 ） n =1 时由前可知，公式成立。 2 ）假设当 n = k ( k ∈ N  ) 时有： S k = , ∴ 当 n = k +1 时公式仍成立 由 1 ）、 2 ）可知 , 对一切 n ∈ N  公式均成立。 数学归纳法 是一种证明与自然数有关的数学命题的重要方法。 其格式主要有两个步骤、一个结论 : (1) 证明当 n 取第一个值 n 0 ( 如 n 0 =1 或 2 等 ) 时结论正确； 验证初始条件 (2) 假设 n = k 时结论正确 , 在假设之下 , 证明 n = k +1 时结论也正确； 假设推理 (3) 由（ 1 ）、（ 2 ）得出结论 . 下结论 2. “ 观察、猜想、证明 ” 是解决与自然数有关的命题的有效途径 . 注意 : 递推基础不可少 , 归纳假设要用到 , 结论写明莫忘掉。 课堂小结： 找准起点 , 奠基要稳 用上假设 递推才真 写明结论 才算完整 练习 1 . 用数学归纳法证明 : 练习 2 . 证明不等式 : 练习 3 : 平面内有 n ( n 2) 条直线，任何两条都不平行，任何三条不过同一点，问交点的个数 为多少 ? 并证明 . 用数学归纳法可以解决许多有关正整数的命题或猜想 ,