人教A数学必修一对数函数及其性质基础知识讲解
对数函数及其性质
【学习目标】
1.理解对数函数的概念,体会对数函数是一类很重要的函数模型;
2.探索对数函数的单调性与特殊点,掌握对数函数的性质,会进行同底对数和不同底对数大小的比较;
3.了解反函数的概念,知道指数函数与对数函数互为反函数.
【要点梳理】
要点一、对数函数的概念
1.函数y=logax(a>0,a≠1)叫做对数函数.其中是自变量,函数的定义域是,值域为.
2.判断一个函数是对数函数是形如的形式,即必须满足以下条件:
(1)系数为1;
(2)底数为大于0且不等于1的常数;
(3)对数的真数仅有自变量.
要点诠释:
(1)只有形如y=logax(a>0,a≠1)的函数才叫做对数函数,像等函数,它们是由对数函数变化得到的,都不是对数函数。
(2)求对数函数的定义域时应注意:①对数函数的真数要求大于零,底数大于零且不等于1;②对含有字母的式子要注意分类讨论。
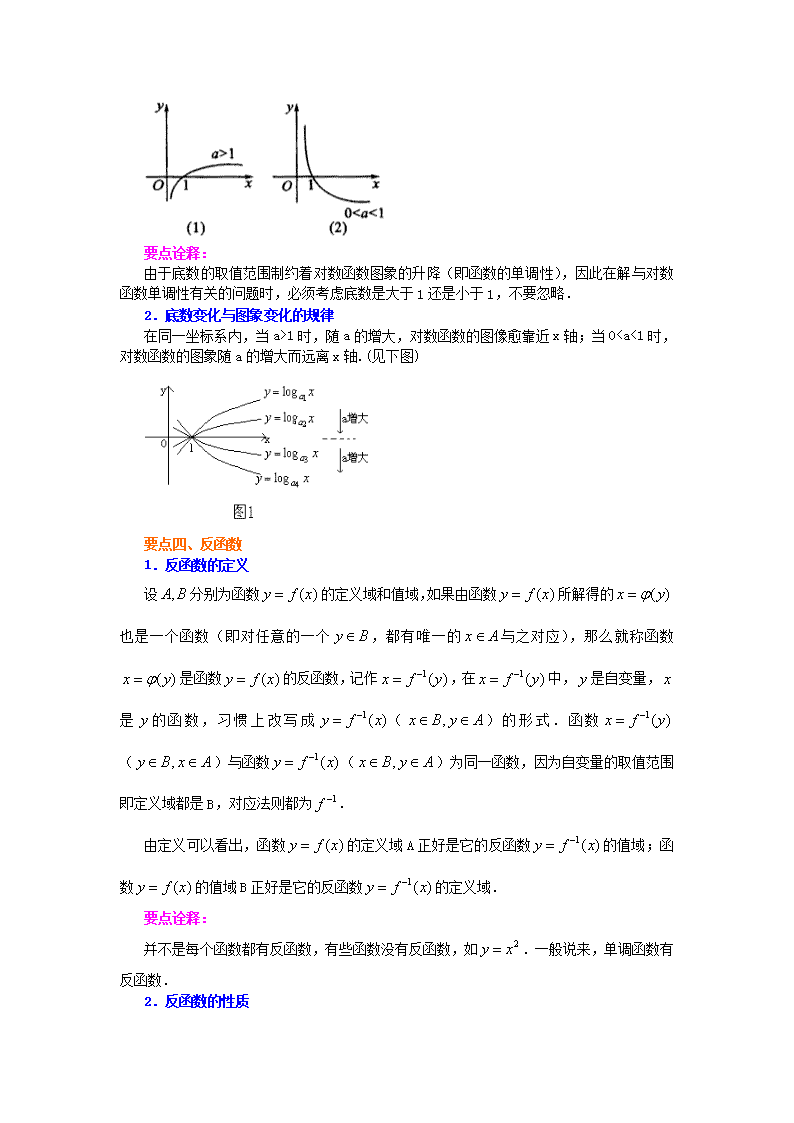
要点二、对数函数的图象与性质
a>0
0<a<1
图象
性质
定义域:(0,+∞)
值域:R
过定点(1,0),即x=1时,y=0
在(0,+∞)上增函数
在(0,+∞)上是减函数
当0<x<1时,y<0,
当x≥1时,y≥0
当0<x<1时,y>0,
当x≥1时,y≤0
要点诠释:
关于对数式logaN的符号问题,既受a的制约又受N的制约,两种因素交织在一起,应用时经常出错.下面介绍一种简单记忆方法,供同学们学习时参考.
以1为分界点,当a,N同侧时,logaN>0;当a,N异侧时,logaN<0.
要点三、底数对对数函数图象的影响
1.底数制约着图象的升降.
如图
要点诠释:
由于底数的取值范围制约着对数函数图象的升降(即函数的单调性),因此在解与对数函数单调性有关的问题时,必须考虑底数是大于1还是小于1,不要忽略.
2.底数变化与图象变化的规律
在同一坐标系内,当a>1时,随a的增大,对数函数的图像愈靠近x轴;当0
;(4) >;(5) 略.
【解析】由数形结合的方法或利用函数的单调性来完成.
(1)解法1:画出对数函数的图象,横坐标为3.6的点在横坐标为8.9的点的下方,所以,;
解法2:由函数在R+上是单调增函数,且3.6<8.9,所以;
(2)与第(1)小题类似,在R+上是单调减函数,且1.9<3.5,所以;
(3)函数和的图象如图所示.当时,的图象在的图象上方,这里,.
(4)
(5) 注:底数是常数,但要分类讨论a的范围,再由函数单调性判断大小.
解法1:当时,在(0,+∞)上是增函数,且5.1<5.9,所以,
当时,y=logax在(0,+∞)上是减函数,且4.2<4.8,所以,
解法2:转化为指数函数,再由指数函数的单调性判断大小,
令,则,令,则
当时,在R上是增函数,且4.2<4.8,
所以,b1b2,即.
【总结升华】比较两个对数值的大小的基本方法是:
(1)比较同底的两个对数值的大小,常利用对数函数的单调性.
(2)比较同真数的两个对数值的大小,常有两种方法:①先利用对数换底公式化为同底的对数,再利用对数函数的单调性和倒数关系比较大小;②利用对数函数图象的互相位置关系比较大小.
(3)若底数与真数都不同,则通过一个恰当的中间量来比较大小.
【高清课堂:对数函数369070 例1】
例4.利用对数函数的性质比较、、的大小.
【答案】
【解析】,,,只需比较与的大小即可
【总结升华】本题也可以使用一个常用的结论:类似于的一个结论,,得出三个数的大小.
举一反三:
【变式1】 已知则( )
A. B. C. D.
【答案】 C
【解析】另,,,在同一坐标系下作出三个函数图像,由图像可得
又∵为单调递增函数,
∴
故选C.
例5.求函数的值域和单调区间.
【思路点拨】先解不等式,保证原式有意义,然后再在定义域范围内求内函数的单调区间,然后根据复合函数的单调性就是内函数与外函数的单调性“同增异减”来求解.
【答案】[-1,+∞;增区间为;减区间为.
【解析】设,则.∵ y=为减函数,且,
∴ ,即函数的值域为[-1,+∞.再由:函数的定义域为,即.
∴ 在上递增而在上递减,而y=为减函数.
∴ 函数的增区间为,减区间为.
【总结升华】对数型复合函数一般可分为两类:一类是对数函数为外函数,即型;另一类是内函数为对数函数,即型.对于型的函数的单调性,有以下结论:函数的单调性与函数的单调性,当时相同,当时相反.
研究型复合函数的单调性,一般用复合法来判定即可.复合函数的单调性就是内函数与外函数的单调性“同增异减”.
研究对数型复合函数的单调性,一定要注意先研究函数的定义域,也就是要坚持“定义域优先”的原则.
举一反三:
【变式1】求函数的值域和单调区间.
【答案】;减区间为,增区间为.
【解析】设,则,∵ y=为增函数,
的值域为.
再由:的定义域为
在上是递增而在上递减,而为增函数
∴ 函数y=的减区间为,增区间为.
类型四、函数的奇偶性
例6. 判断下列函数的奇偶性.
(1) (2).
【思路点拨】判断函数奇偶性的步骤是:(1)先求函数的定义域,如果定义域关于原点对称,则进行(2),如果定义域不关于原点对称,则函数为非奇非偶函数。(2)求,如果,则函数是偶函数,如果,则函数是奇函数。
【答案】(1)奇函数;(2)奇函数.
【解析】首先要注意定义域的考查,然后严格按照证明奇偶性基本步骤进行.
(1)由
所以函数的定义域为:(-2,2)关于原点对称
又
所以函数是奇函数;
【总结升华】此题确定定义域即解简单分式不等式,函数解析式恒等变形需利用对数的运算性质.说明判断对数形式的复合函数的奇偶性,不能轻易直接下结论,而应注意对数式的恒等变形.
(2)由
所以函数的定义域为R关于原点对称
又
即f(-x)=-f(x);所以函数.
【总结升华】此题定义域的确定可能稍有困难,函数解析式的变形用到了分子有理化的技巧,要求掌握.
类型五、反函数
例7.求出下列函数的反函数
(1);(2).
【答案】(1);(2)
【解析】(1)对数函数,它的底数为,所以它的反函数是指数函数;
(2)指数函数的反函数是对数函数。
【总结升华】
反函数的定义域都由原函数的值域来确定的,特别是当反函数的定义域与由反函数解析式有意义所确定的自变量的取值范围不一致时,一定要注明反函数的定义域.
举一反三:
【高清课堂:对数函数369070 例5】
【变式1】 若函数是函数且a≠1)的反函数,且,则( )
(A) (B) (C) (D)2
【答案】 A
【解析】解法1:函数是函数且a≠1)的反函数
,又
,,
故选A.
解法2:函数是函数且a≠1)的反函数,且
点(1,2)在函数的图象上,
故选A.
类型六、利用函数图象解不等式
例8.若不等式,当时恒成立,求实数a的取值范围.
【思路点拨】画出函数的图象与函数的图象,然后借助图象去求借。
【答案】
【解析】 要使不等式在时恒成立,即函数的图在内恒在函数图象的上方,而图象过点.由右图可知,,显然这里0<a<1,∴函数递减.又,∴,即.∴所求的a的取值范围为.
【总结升华】“数”是数学的特征,它精确、量化,最有说服力;而“形”则形象、直观,能简化思维过程,降低题目的难度,简化解题过程,把它们的优点集中在一起就是最佳组合.本例中,利用图形的形象直观快速地得到答案,简化了解题过程.正因为如此,数形结合成为中学数学的四个最基本的数学思想方法之一,因此我们必须熟练地掌握这一思想方法,并能灵活地运用它来分析和解决问题.
在涉及方程与不等式的问题时,往往构造两个函数与,则=的实数解等价于两个函数与的图象的交点的横坐标;而的的解等价于函数的图象在的图象下方的点的横坐标的取值范围.利用图象的形象性、直观性,可使问题得到顺利地解决,而且分散了问题解决的难度、简化了思维过程.因此,我们要善于用数形结合的方法来解决方程与不等式的问题.
举一反三:
【变式1】 当x∈(1,2)时,不等式恒成立,求a的取值范围.
【答案】1<a≤2
【解析】设,,要使当x∈(1,2)时,不等式恒成立,只需在(1,2)上的图象在的下方即可.当0<a<1时,由图象知显然不成立.当a>1时,如图2-2-5所示,要使在(1,2)上,的图象在的下方,
只需,
即,,∴1<a≤2.
类型七、对数函数性质的综合应用
例9.(1)已知函数的定义域为,求实数的取值范围;
(2)已知函数的值域为,,求实数的取值范围;
(3)的定义域为,求实数的取值范围.
【思路点拨】与求函数定义域、值域的常规问题相比,本题属非常规问题,关键在于转化成常规问题.的定义域为R,即关于的不等式的解集为R,这是不等式中的常规问题.
的值域为R与恒为正值是不等价的,因为这里要求取遍一切实数,即要求取遍一切正数,考察此函数的图象的各种情况,如图,我们会发现,使能取遍一切正数的条件是.
【答案】(1);(2);(3).
【解析】与求函数定义域、值域的常规问题相比,本题属非常规问题,关键在于转化成常规问题.的定义域为R,即关于的不等式的解集为R,这是不等式中的常规问题.
的值域为R与恒为正值是不等价的,因为这里要求取遍一切实数,即要求取遍一切正数,考察此函数的图象的各种情况,我们会发现,使能取遍一切正数的条件是.
(1)的定义域为R,
恒成立,,.
(2)的值域为R,
取遍一切正数,,.
(3)由题意,问题可等价转化为不等式的解集为,记作图形,如图所示,只需过点,,即满足,且即可,解得.
【总结升华】如果函数的定义域为某个区间D,则函数在这个区间D的任何子集内部都有意义;如果函数在区间E上有意义,而的定义域为D,则必有.
举一反三:
【变式1】 已知函数.
(1)若函数的定义域为R,求实数的取值范围;(2)若函数的值域为R,求实数的取值范围.
【答案】(1)a>1;(2)0≤a≤1.
【解析】(1) 的定义域为R,即:关于x的不等式的解集为R,
当a=0时,此不等式变为2x+1>0,其解集不是R;
当a≠0时,有 a>1.∴ a的取值范围为a>1.
(2)f(x)的值域为R,即u=ax2+2x+1能取遍一切正数 a=0或0≤a≤1,
∴ a的取值范围为0≤a≤1.