2015年高考数学（理科）真题分类汇编N单元 选修4系列

2015年高考数学（理科）真题分类汇编N单元 选修4系列

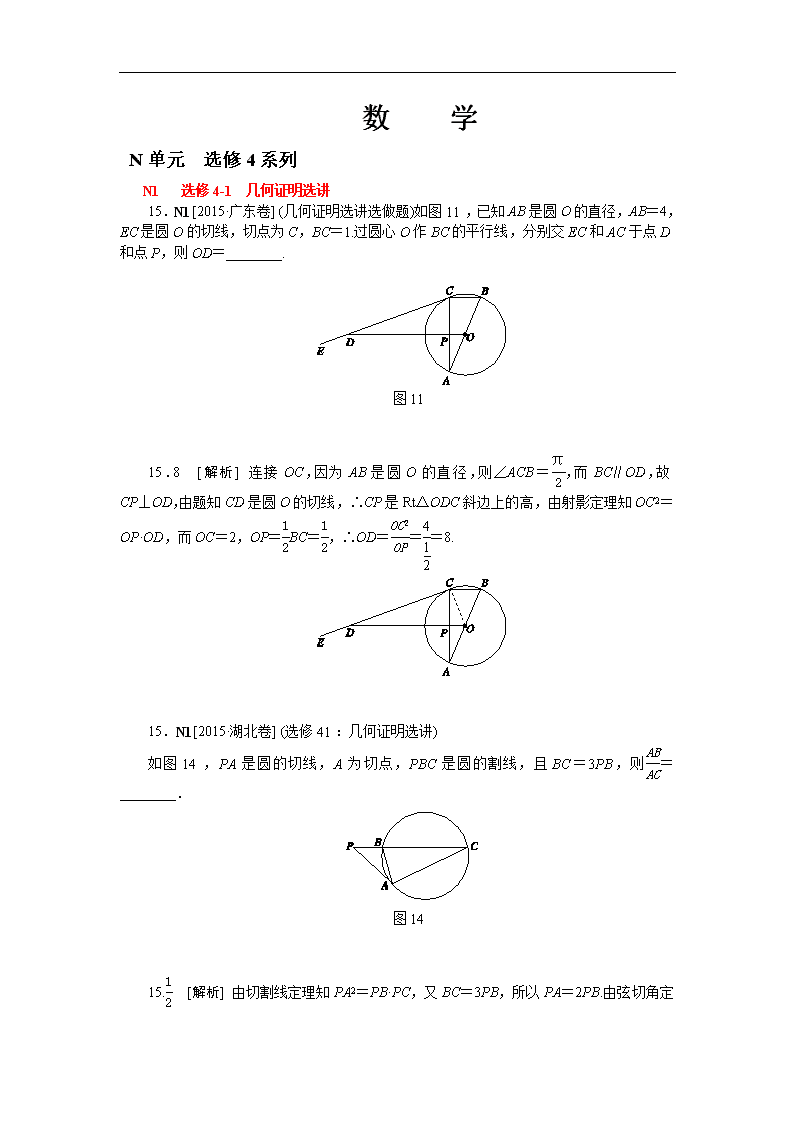
‎ 数 学 N单元 选修4系列 ‎ N1 选修4-1 几何证明选讲 ‎15．N1[2015·广东卷] (几何证明选讲选做题)如图11，已知AB是圆O的直径，AB＝4，EC是圆O的切线，切点为C，BC＝1.过圆心O作BC的平行线，分别交EC和AC于点D和点P，则OD＝________.‎ 图11‎ ‎15．8　[解析] 连接OC，因为AB是圆O的直径，则∠ACB＝，而BC∥OD，故CP⊥OD，由题知CD是圆O的切线，∴CP是Rt△ODC斜边上的高，由射影定理知OC2＝OP·OD，而OC＝2，OP＝BC＝，∴OD＝＝＝8.‎ ‎15．N1[2015·湖北卷] (选修41：几何证明选讲)‎ 如图14，PA是圆的切线，A为切点，PBC是圆的割线，且BC＝3PB，则＝________．‎ 图14‎ ‎15.　[解析] 由切割线定理知PA2＝PB·PC，又BC＝3PB，所以PA＝2PB ‎.由弦切角定理知∠PAB＝∠PCA，又∠APC＝∠BPA，所以△PAB∽△PCA，所以＝＝.‎ ‎21．N1[2015·江苏卷] A．[选修41：几何证明选讲]如图15，在△ABC中，AB＝AC，△ABC的外接圆⊙O的弦AE交BC于点D.‎ 求证：△ABD∽△AEB.‎ 图15‎ N2B.[选修42：矩阵与变换]已知x，y∈R，向量α＝是矩阵A＝的属于特征值－2的一个特征向量，求矩阵A以及它的另一个特征值．‎ N‎3C.[选修44：坐标系与参数方程]已知圆C的极坐标方程为ρ2＋2ρsin－4＝0，求圆C的半径．‎ N4D.[选修45：不等式选讲]解不等式x＋|2x＋3|≥2.‎ ‎21．A.证明：因为AB＝AC，所以∠ABD＝∠C.‎ 又因为∠C＝∠E，所以∠ABD＝∠E，‎ 又∠BAE为公共角，所以△ABD∽△AEB.‎ B．解：由已知，得Aα＝－2α，即＝＝，则即所以矩阵A＝.‎ 从而矩阵A的特征多项式f(λ)＝(λ＋2)(λ－1)，‎ 所以矩阵A的另一个特征值为1.‎ C．解：以极坐标系的极点为平面直角坐标系的原点O，以极轴为x轴的正半轴，建立直角坐标系xOy.‎ 圆C的极坐标方程为ρ2＋2ρ－4＝0，化简得ρ2＋2ρsin θ－2ρcos θ－4＝0，‎ 则圆C的直角坐标方程为x2＋y2－2x＋2y－4＝0，‎ 即(x－1)2＋(y＋1)2＝6，‎ 所以圆C的半径为.‎ D．解：原不等式可化为或 解得x≤－5或x≥－.‎ 综上，原不等式的解集是.‎ ‎22．N1[2015·全国卷Ⅱ] 选修41：几何证明选讲 如图18，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．‎ ‎(1)证明：EF∥BC；‎ ‎(2)若AG等于⊙O的半径，且AE＝MN＝2，求四边形EBCF的面积．‎ 图18‎ ‎22．解：(1)证明：由于△ABC是等腰三角形，AD⊥BC，所以AD是∠CAB的平分线．又因为⊙O分别与AB，AC相切于点E，F，所以AE＝AF，故AD⊥EF，从而EF∥BC.‎ ‎(2)由(1)知，AE＝AF，AD⊥EF，故AD是EF的垂直平分线．又EF为⊙O的弦，所以O在AD上．‎ 连接OE，OM，则OE⊥AE.‎ 由AG等于⊙O的半径得AO＝2OE，所以∠OAE＝30°.因此△ABC和△AEF都是等边三角形．‎ 因为AE＝2，所以AO＝4，OE＝2.‎ 因为OM＝OE＝2，DM＝MN＝，所以OD＝1.于是AD＝5，AB＝.‎ 所以四边形EBCF的面积为××－×(2)2×＝.‎ ‎22．N1[2015·全国卷Ⅰ] 选修41：几何证明选讲 如图17，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E.‎ ‎(1)若D为AC的中点，证明：DE是⊙O的切线；‎ ‎(2)若OA＝CE，求∠ACB的大小．‎ 图17‎ ‎22．解：(1)证明：连接AE，由已知得，AE⊥BC，AC⊥AB.‎ 在Rt△AEC中，由已知得，DE＝DC，故∠DEC＝∠DCE.‎ 连接OE，则∠OBE＝∠OEB.‎ 又∠ACB＋∠ABC＝90°，所以∠DEC＋∠OEB＝90°，故∠OED＝90°，即DE是⊙O的切线．‎ ‎(2)设CE＝1，AE＝x，由已知得AB＝2，BE＝.‎ 由射影定理可得，AE2＝CE·BE，所以x2＝，即x4＋x2－12＝0，‎ 可得x＝，所以∠ACB＝60°.‎ N2 选修4-2 矩阵 ‎21．N1[2015·江苏卷] A．[选修41：几何证明选讲]如图15，在△ABC中，AB＝AC，△ABC的外接圆⊙O的弦AE交BC于点D.‎ 求证：△ABD∽△AEB.‎ 图15‎ N2B.[选修42：矩阵与变换]已知x，y∈R，向量α＝是矩阵A＝的属于特征值－2的一个特征向量，求矩阵A以及它的另一个特征值．‎ N‎3C.[选修44：坐标系与参数方程]已知圆C的极坐标方程为ρ2＋2ρsin－4＝0，求圆C的半径．‎ N4D.[选修45：不等式选讲]解不等式x＋|2x＋3|≥2.‎ ‎21．A.证明：因为AB＝AC，所以∠ABD＝∠C.‎ 又因为∠C＝∠E，所以∠ABD＝∠E，‎ 又∠BAE为公共角，所以△ABD∽△AEB.‎ B．解：由已知，得Aα＝－2α，即＝＝，则即所以矩阵A＝.‎ 从而矩阵A的特征多项式f(λ)＝(λ＋2)(λ－1)，‎ 所以矩阵A的另一个特征值为1.‎ C．解：以极坐标系的极点为平面直角坐标系的原点O，以极轴为x轴的正半轴，建立直角坐标系xOy.‎ 圆C的极坐标方程为ρ2＋2ρ－4＝0，化简得ρ2＋2ρsin θ－2ρcos θ－4＝0，‎ 则圆C的直角坐标方程为x2＋y2－2x＋2y－4＝0，‎ 即(x－1)2＋(y＋1)2＝6，‎ 所以圆C的半径为.‎ D．解：原不等式可化为或 解得x≤－5或x≥－.‎ 综上，原不等式的解集是.‎ ‎21．N2、N3、N4[2015·福建卷] (1)选修42：矩阵与变换 已知矩阵A＝)，B＝))．‎ ‎(i)求A的逆矩阵A－1；‎ ‎(ii)求矩阵C，使得AC＝B.‎ ‎(2)选修44：坐标系与参数方程 在平面直角坐标系xOy中，圆C的参数方程为(t为参数)．在极坐标系(与平面直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴)中，直线l的方程为ρsin＝m(m∈R)．‎ ‎(i)求圆C的普通方程及直线l的直角坐标方程；‎ ‎(ii)设圆心C到直线l的距离等于2，求m的值．‎ ‎(3)选修45：不等式选讲 已知a＞0，b＞0，c＞0，函数f(x)＝|x＋a|＋|x－b|＋c的最小值为4.‎ ‎(i)求a＋b＋c的值；‎ ‎(ii)求a2＋b2＋c2的最小值．‎ ‎21．解：(1)(i)因为|A|＝2×3－1×4＝2，‎ 所以A－1＝))‎ ‎＝))．‎ ‎(ii)由AC＝B得(A－‎1A)C＝A－1B，故 C＝A－1B ‎＝))))‎ ‎＝,),－3)))．‎ ‎(2)(i)消去参数t，得到圆C的普通方程为(x－1)2＋(y＋2)2＝9.‎ 由ρsin＝m，得 ρsin θ－ρcos θ－m＝0.‎ 所以直线l的直角坐标方程为x－y＋m＝0.‎ ‎(ii)依题意，圆心C到直线l的距离等于2，‎ 即＝2，解得m＝－3±2.‎ ‎(3)(i)因为f(x)＝|x＋a|＋|x－b|＋c≥|(x＋a)－(x－b)|＋c＝|a＋b|＋c，‎ 当且仅当－a≤x≤b时，等号成立，‎ 又a＞0，b＞0，所以|a＋b|＝a＋b，‎ 所以f(x)的最小值为a＋b＋c.‎ 又已知f(x)的最小值为4，‎ 所以a＋b＋c＝4.‎ ‎(ii)由(i)知a＋b＋c＝4，由柯西不等式得 (4＋9＋1)≥＝(a＋b＋c)2＝16，‎ 即a2＋b2＋c2≥，‎ 当且仅当＝＝，即a＝，b＝，c＝时等号成立．‎ 故a2＋b2＋c2的最小值为.‎ N3 选修4-4 参数与参数方程 ‎12．N3[2015·安徽卷] 在极坐标系中，圆ρ＝8sin θ上的点到直线θ＝(ρ∈R)距离的最大值是________．‎ ‎12．6　[解析] 依题意得圆的直角坐标方程为x2＋y2－8y＝0，即x2＋(y－4)2＝16，直线的直角坐标方程为x－y＝0，故圆心到直线的距离d＝＝2，因此圆上的点到直线的最大距离为d＋r＝6.‎ ‎14．N3[2015·广东卷] (坐标系与参数方程选做题)已知直线l的极坐标方程为2ρsin＝，点A的极坐标为A，则点A到直线l的距离为________．‎ ‎14.　[解析] 直线l的极坐标方程2ρsin＝化为直角坐标方程为x－y＋1＝0，A在直角坐标系中的坐标为，即A(2，－2)，故点A到直线的距离为 eq f(|1×2－1×（－2）＋1|, (2))＝.‎ ‎16．N3[2015·湖北卷] (选修44：坐标系与参数方程)‎ 在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρ(sin θ－3cos θ)＝0，曲线C的参数方程为(t为参数)，l与C相交于A，B两点，则|AB|＝________．‎ ‎16．2　[解析] 将直线l的极坐标方程ρ(sin θ－3cos θ)＝0化为直角坐标方程为3x－y＝0，将曲线C的参数方程(t为参数)化为普通方程为y2－x2＝4.联立 解得或 不妨设点A，B，所以＝＝2.‎ ‎21．N1[2015·江苏卷] A．[选修41：几何证明选讲]如图15，在△ABC中，AB＝AC，△ABC的外接圆⊙O的弦AE交BC于点D.‎ 求证：△ABD∽△AEB.‎ 图15‎ N2B.[选修42：矩阵与变换]已知x，y∈R，向量α＝是矩阵A＝的属于特征值－2的一个特征向量，求矩阵A以及它的另一个特征值．‎ N‎3C.[选修44：坐标系与参数方程]已知圆C的极坐标方程为ρ2＋2ρsin－4＝0，求圆C的半径．‎ N4D.[选修45：不等式选讲]解不等式x＋|2x＋3|≥2.‎ ‎21．A.证明：因为AB＝AC，所以∠ABD＝∠C.‎ 又因为∠C＝∠E，所以∠ABD＝∠E，‎ 又∠BAE为公共角，所以△ABD∽△AEB.‎ B．解：由已知，得Aα＝－2α，即＝＝，则即所以矩阵A＝.‎ 从而矩阵A的特征多项式f(λ)＝(λ＋2)(λ－1)，‎ 所以矩阵A的另一个特征值为1.‎ C．解：以极坐标系的极点为平面直角坐标系的原点O，以极轴为x轴的正半轴，建立直角坐标系xOy.‎ 圆C的极坐标方程为ρ2＋2ρ－4＝0，化简得ρ2＋2ρsin θ－2ρcos θ－4＝0，‎ 则圆C的直角坐标方程为x2＋y2－2x＋2y－4＝0，‎ 即(x－1)2＋(y＋1)2＝6，‎ 所以圆C的半径为.‎ D．解：原不等式可化为或 解得x≤－5或x≥－.‎ 综上，原不等式的解集是.‎ ‎23．N3[2015·全国卷Ⅱ] 选修44：坐标系与参数方程 在直角坐标系xOy中，曲线C1：(t为参数，t≠0)，其中0≤α<π.在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sin θ，C3：ρ＝2cos θ.‎ ‎(1)求C2与C3交点的直角坐标；‎ ‎(2)若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．‎ ‎23．解：(1)曲线C2的直角坐标方程为x2＋y2－2y＝0，曲线C3的直角坐标方程为x2＋y2－2x＝0.‎ 联立解得或 所以C2与C3交点的直角坐标为(0，0)和.‎ ‎(2)曲线C1的极坐标方程为θ＝α(ρ∈R，ρ≠0)，其中0≤α<π.‎ 因此A的极坐标为(2sin α，α)，‎ B的极坐标为(2cos α，α)，‎ 所以|AB|＝|2sin α－2cos α|＝4sin.‎ 故当α＝时，|AB|取得最大值，最大值为4.‎ ‎23．N3[2015·全国卷Ⅰ] 选修44：坐标系与参数方程 在直角坐标系xOy中，直线C1：x＝－2，圆C2：(x－1)2＋(y－2)2＝1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．‎ ‎(1)求C1，C2的极坐标方程；‎ ‎(2)若直线C3的极坐标方程为θ＝(ρ∈R)，设C2与C3的交点为M，N，求△C2MN的面积．‎ ‎23．解：(1)因为x＝ρcos θ，y＝ρsin θ，所以C1的极坐标方程为ρcos θ＝－2，C2的极坐标方程为ρ2－2ρcos θ－4ρsin θ＋4＝0.‎ ‎(2)将θ＝代入ρ2－2ρcos θ－4ρsin θ＋4＝0，得ρ2－3ρ＋4＝0，解得ρ1＝2，ρ2＝.故ρ1－ρ2＝，即|MN|＝.‎ 又C2的半径为1，所以△C2MN的面积为.‎ ‎11．N3[2015·北京卷] 在极坐标系中，点到直线ρ(cos θ＋sin θ)＝6的距离为________．‎ ‎11．1　[解析] 利用公式把极坐标转化为平面直角坐标(1，)，把直线方程ρ(cos θ＋sin θ)＝6转化为x＋y－6＝0.利用点到直线的距离公式可知，d＝＝1.‎ ‎21．N2、N3、N4[2015·福建卷] (1)选修42：矩阵与变换 已知矩阵A＝)，B＝))．‎ ‎(i)求A的逆矩阵A－1；‎ ‎(ii)求矩阵C，使得AC＝B.‎ ‎(2)选修44：坐标系与参数方程 在平面直角坐标系xOy中，圆C的参数方程为(t为参数)．在极坐标系(与平面直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴)中，直线l的方程为ρsin＝m(m∈R)．‎ ‎(i)求圆C的普通方程及直线l的直角坐标方程；‎ ‎(ii)设圆心C到直线l的距离等于2，求m的值．‎ ‎(3)选修45：不等式选讲 已知a＞0，b＞0，c＞0，函数f(x)＝|x＋a|＋|x－b|＋c的最小值为4.‎ ‎(i)求a＋b＋c的值；‎ ‎(ii)求a2＋b2＋c2的最小值．‎ ‎21．解：(1)(i)因为|A|＝2×3－1×4＝2，‎ 所以A－1＝))‎ ‎＝))．‎ ‎(ii)由AC＝B得(A－‎1A)C＝A－1B，故 C＝A－1B ‎＝))))‎ ‎＝,),－3)))．‎ ‎(2)(i)消去参数t，得到圆C的普通方程为(x－1)2＋(y＋2)2＝9.‎ 由ρsin＝m，得 ρsin θ－ρcos θ－m＝0.‎ 所以直线l的直角坐标方程为x－y＋m＝0.‎ ‎(ii)依题意，圆心C到直线l的距离等于2，‎ 即＝2，解得m＝－3±2.‎ ‎(3)(i)因为f(x)＝|x＋a|＋|x－b|＋c≥|(x＋a)－(x－b)|＋c＝|a＋b|＋c，‎ 当且仅当－a≤x≤b时，等号成立，‎ 又a＞0，b＞0，所以|a＋b|＝a＋b，‎ 所以f(x)的最小值为a＋b＋c.‎ 又已知f(x)的最小值为4，‎ 所以a＋b＋c＝4.‎ ‎(ii)由(i)知a＋b＋c＝4，由柯西不等式得 (4＋9＋1)≥＝(a＋b＋c)2＝16，‎ 即a2＋b2＋c2≥，‎ 当且仅当＝＝，即a＝，b＝，c＝时等号成立．‎ 故a2＋b2＋c2的最小值为.‎ N4 选修4-5 不等式选讲 ‎5．A2、N4、D3[2015·湖北卷] 设a1，a2，…，an∈R，n≥3.若p：a1，a2，…，an成等比数列；q：(a＋a＋…＋a)(a＋a＋…＋a)＝(a‎1a2＋a‎2a3＋…＋an－1an)2，则(　　)‎ A．p是q的充分条件，但不是q的必要条件 B．p是q的必要条件，但不是q的充分条件 C．p是q的充分必要条件 D．p既不是q的充分条件，也不是q的必要条件 ‎5．A　[解析] 当p成立，即a1，a2，…，an成等比数列时，＝＝…＝，满足柯西不等式(a＋a＋…＋a)(a＋a＋…＋a)≥(a‎1a2＋a‎2a3＋…＋an－1an)2等号成立的条件，故(a＋a＋…＋a)(a＋a＋…＋a)＝(a‎1a2＋a‎2a3＋…＋ an－1an)2，即q成立；但当q成立时，不一定非要a1，a2，…，an成等比数列，如：当a1＝1，a2＝a3＝…＝an＝0时，q成立，但不满足a1，a2，…，an成等比数列．所以p是q的充分条件，但不是q的必要条件．故选A.‎ ‎21．N1[2015·江苏卷] A．[选修41：几何证明选讲]如图15，在△ABC中，AB＝AC，△ABC的外接圆⊙O的弦AE交BC于点D.‎ 求证：△ABD∽△AEB.‎ 图15‎ N2B.[选修42：矩阵与变换]已知x，y∈R，向量α＝是矩阵A＝的属于特征值－2的一个特征向量，求矩阵A以及它的另一个特征值．‎ N‎3C.[选修44：坐标系与参数方程]已知圆C的极坐标方程为ρ2＋2ρsin－4＝0，求圆C的半径．‎ N4D.[选修45：不等式选讲]解不等式x＋|2x＋3|≥2.‎ ‎21．A.证明：因为AB＝AC，所以∠ABD＝∠C.‎ 又因为∠C＝∠E，所以∠ABD＝∠E，‎ 又∠BAE为公共角，所以△ABD∽△AEB.‎ B．解：由已知，得Aα＝－2α，即＝＝，则即所以矩阵A＝.‎ 从而矩阵A的特征多项式f(λ)＝(λ＋2)(λ－1)，‎ 所以矩阵A的另一个特征值为1.‎ C．解：以极坐标系的极点为平面直角坐标系的原点O，以极轴为x轴的正半轴，建立直角坐标系xOy.‎ 圆C的极坐标方程为ρ2＋2ρ－4＝0，化简得ρ2＋2ρsin θ－2ρcos θ－4＝0，‎ 则圆C的直角坐标方程为x2＋y2－2x＋2y－4＝0，‎ 即(x－1)2＋(y＋1)2＝6，‎ 所以圆C的半径为.‎ D．解：原不等式可化为或 解得x≤－5或x≥－.‎ 综上，原不等式的解集是.‎ ‎24．N4[2015·全国卷Ⅱ] 选修45：不等式选讲 设a，b，c，d均为正数，且a＋b＝c＋d，证明：‎ ‎(1)若ab>cd，则＋>＋；‎ ‎(2)＋>＋是|a－b|<|c－d|的充要条件．‎ ‎24．证明：(1)(＋)2＝a＋b＋2，‎ ‎(＋)2＝c＋d＋2，‎ 由题设a＋b＝c＋d，ab>cd，‎ 得(＋)2>(＋)2，‎ 因此＋>＋.‎ ‎(2)(i)若|a－b|<|c－d|，则(a－b)2<(c－d)2，即 ‎(a＋b)2－4ab<(c＋d)2－4cd.‎ 因为a＋b＝c＋d，所以ab>cd.‎ 由(1)得＋>＋.‎ ‎(ii)若＋>＋，‎ 则(＋)2>(＋)2，‎ 即a＋b＋2>c＋d＋2.‎ 因为a＋b＝c＋d，所以ab>cd.于是 ‎(a－b)2＝(a＋b)2－4ab<(c＋d)2－4cd＝(c－d)2，‎ 因此|a－b|<|c－d|.‎ 综上，＋>＋是|a－b|<|c－d|的充要条件．‎ ‎24．N4[2015·全国卷Ⅰ] 选修45：不等式选讲 已知函数f(x)＝|x＋1|－2|x－a|，a>0.‎ ‎(1)当a＝1时，求不等式f(x)>1的解集；‎ ‎(2)若f(x)的图像与x轴围成的三角形面积大于6，求a的取值范围．‎ ‎24．解：(1)当a＝1时，f(x)>1化为|x＋1|－2|x－1|－1>0.‎ 当x≤－1时，不等式化为x－4>0，无解；‎ 当－10，解得0，解得1≤x<2.‎ 所以f(x)>1的解集为.‎ ‎(2)由题设可得，f(x)＝ 所以函数f(x)的图像与x轴围成的三角形的三个顶点分别为A，B(‎2a＋1，0)，C(a，a＋1)，△ABC的面积为(a＋1)2.‎ 由题设得(a＋1)2>6，故a>2.‎ 所以a的取值范围为(2，＋∞)．‎ ‎21．N2、N3、N4[2015·福建卷] (1)选修42：矩阵与变换 已知矩阵A＝)，B＝))．‎ ‎(i)求A的逆矩阵A－1；‎ ‎(ii)求矩阵C，使得AC＝B.‎ ‎(2)选修44：坐标系与参数方程 在平面直角坐标系xOy中，圆C的参数方程为(t为参数)．在极坐标系(与平面直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴)中，直线l的方程为ρsin＝m(m∈R)．‎ ‎(i)求圆C的普通方程及直线l的直角坐标方程；‎ ‎(ii)设圆心C到直线l的距离等于2，求m的值．‎ ‎(3)选修45：不等式选讲 已知a＞0，b＞0，c＞0，函数f(x)＝|x＋a|＋|x－b|＋c的最小值为4.‎ ‎(i)求a＋b＋c的值；‎ ‎(ii)求a2＋b2＋c2的最小值．‎ ‎21．解：(1)(i)因为|A|＝2×3－1×4＝2，‎ 所以A－1＝))‎ ‎＝))．‎ ‎(ii)由AC＝B得(A－‎1A)C＝A－1B，故 C＝A－1B ‎＝))))‎ ‎＝,),－3)))．‎ ‎(2)(i)消去参数t，得到圆C的普通方程为(x－1)2＋(y＋2)2＝9.‎ 由ρsin＝m，得 ρsin θ－ρcos θ－m＝0.‎ 所以直线l的直角坐标方程为x－y＋m＝0.‎ ‎(ii)依题意，圆心C到直线l的距离等于2，‎ 即＝2，解得m＝－3±2.‎ ‎(3)(i)因为f(x)＝|x＋a|＋|x－b|＋c≥|(x＋a)－(x－b)|＋c＝|a＋b|＋c，‎ 当且仅当－a≤x≤b时，等号成立，‎ 又a＞0，b＞0，所以|a＋b|＝a＋b，‎ 所以f(x)的最小值为a＋b＋c.‎ 又已知f(x)的最小值为4，‎ 所以a＋b＋c＝4.‎ ‎(ii)由(i)知a＋b＋c＝4，由柯西不等式得 (4＋9＋1)≥＝(a＋b＋c)2＝16，‎ 即a2＋b2＋c2≥，‎ 当且仅当＝＝，即a＝，b＝，c＝时等号成立．‎ 故a2＋b2＋c2的最小值为.‎ N5 优选法与试验设计 ‎ ‎