2016届高考数学（理）大一轮复习达标训练试题：板块命题点专练(十六)　算法、统计与统计案例

2016届高考数学（理）大一轮复习达标训练试题：板块命题点专练(十六)　算法、统计与统计案例

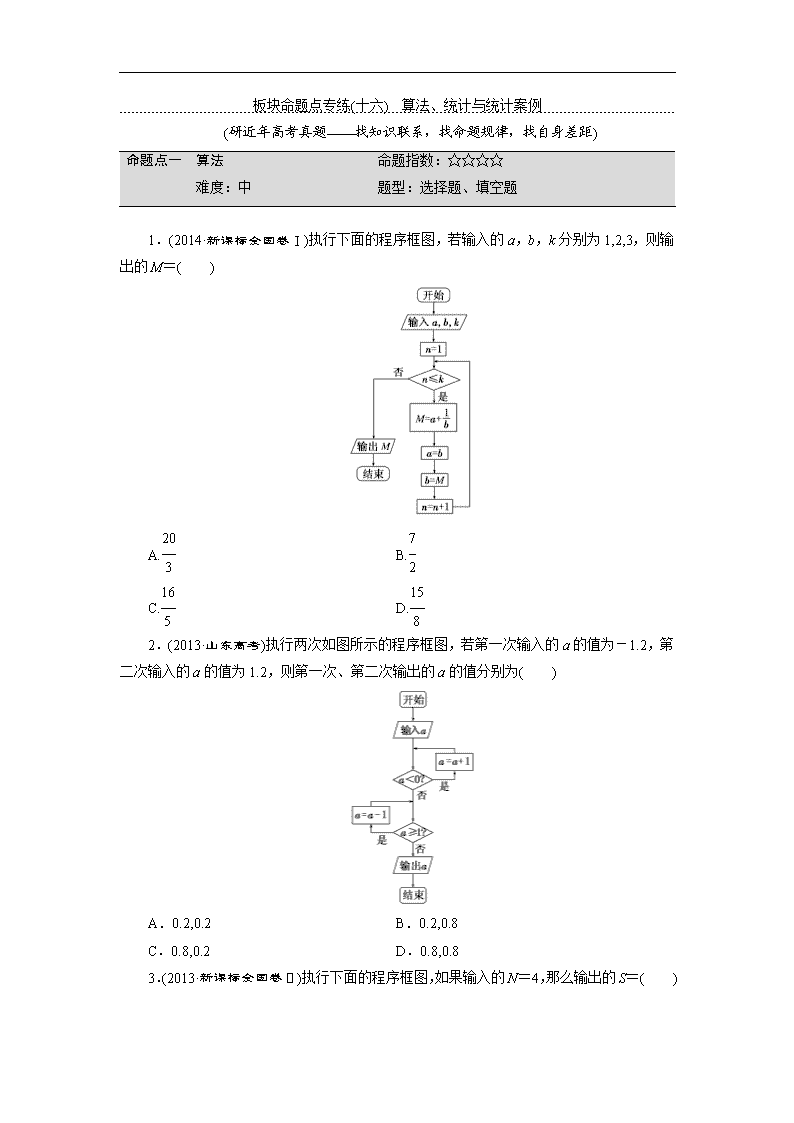
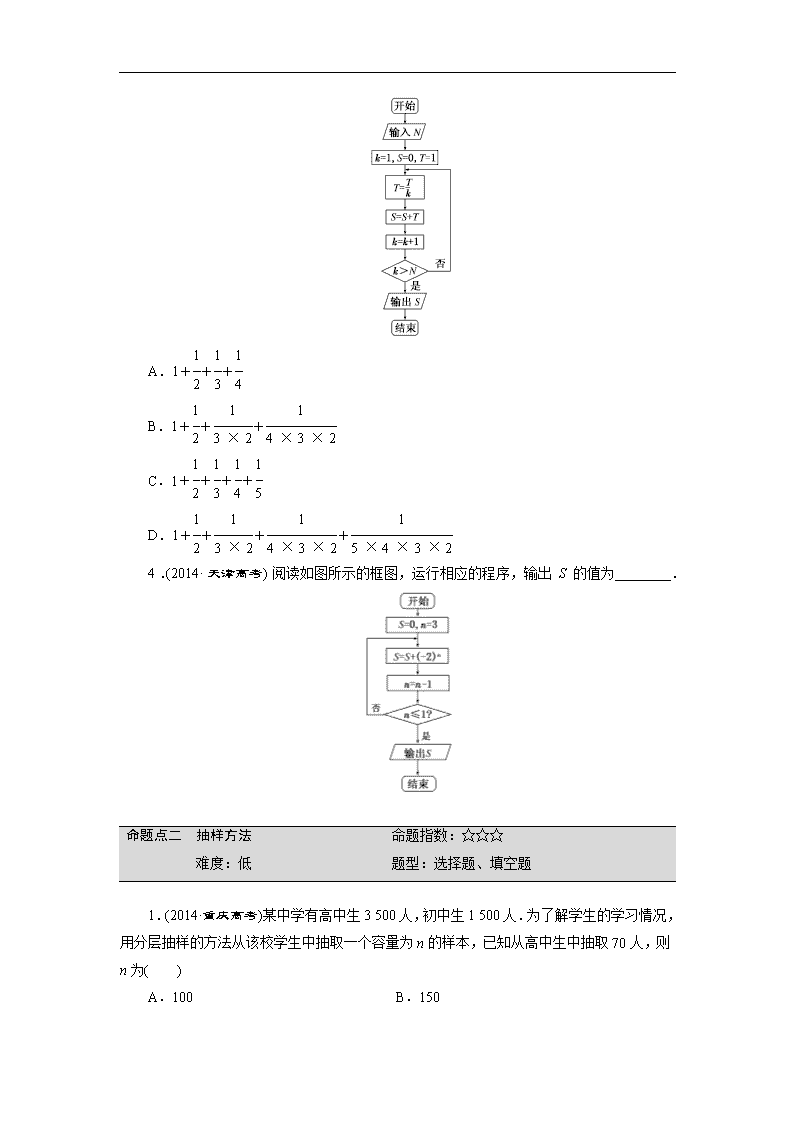
‎ 板块命题点专练(十六)　算法、统计与统计案例 ‎ ‎(研近年高考真题——找知识联系，找命题规律，找自身差距)‎ 命题点一　算法 命题指数：☆☆☆☆‎ 难度：中 题型：选择题、填空题　　‎ ‎1．(2014·新课标全国卷Ⅰ)执行下面的程序框图，若输入的a，b，k分别为1,2,3，则输出的M＝(　　)‎ A.　　　　　　　　　　 B. C. D. ‎2．(2013·山东高考)执行两次如图所示的程序框图，若第一次输入的a的值为－1.2，第二次输入的a的值为1.2，则第一次、第二次输出的a的值分别为(　　)‎ A．0.2,0.2 B．0.2,0.8‎ C．0.8,0.2 D．0.8,0.8‎ ‎3．(2013·新课标全国卷Ⅱ)执行下面的程序框图，如果输入的N＝4，那么输出的S＝(　　)‎ A．1＋＋＋ B．1＋＋＋ C．1＋＋＋＋ D．1＋＋＋＋ ‎4．(2014·天津高考)阅读如图所示的框图，运行相应的程序，输出 S的值为________．‎ 命题点二　抽样方法 命题指数：☆☆☆‎ 难度：低 题型：选择题、填空题　　‎ ‎1．(2014·重庆高考)某中学有高中生3 500人，初中生1 500人．为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n的样本，已知从高中生中抽取70人，则n为(　　)‎ A．100 B．150‎ C．200 D．250‎ ‎2．(2013·陕西高考)某单位有840名职工，现采用系统抽样方法抽取42人做问卷调查，将840人按1,2，…，840随机编号，则抽取的42人中，编号落入区间[481,720]的人数为(　　)‎ A．11 B．12‎ C．13 D．14‎ 命题点三　用样本估计总体 命题指数：☆☆☆☆☆‎ 难度：中 题型：选择题、填空题、解答题 ‎1．(2014·四川高考)在“世界读书日”前夕，为了了解某地5 000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析．在这个问题中，5 000名居民的阅读时间的全体是(　　)‎ A．总体 B．个体 C．样本的容量 D．从总体中抽取的一个样本 ‎2．(2014·山东高考)为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据(单位：kPa)的分组区间为[12,13)，[13,14)，[14,15)，[15,16)，[16,17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组．如图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为(　　)‎ A．6 B．8‎ C．12 D．18‎ ‎3．(2014·陕西高考)某公司10位员工的月工资(单位：元)为x1，x2，…，x10 ，其均值和方差分别为和s2，若从下月起每位员工的月工资增加100元，则这10位员工下月工资的均值和方差分别为(　　)‎ A. ，s2＋1002　　　　　　 B. ＋100, s2＋1002‎ C. ，s2 D. ＋100, s2‎ ‎4．(2012·广东高考)某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．‎ ‎(1)求图中x的值；‎ ‎(2)从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上(含90分)的人数记为ξ，求ξ的数学期望．‎ 命题点四　回归分析与独立性检验 命题指数：☆☆☆‎ 难度：中 题型：选择题、填空题、解答题 ‎1．(2014·重庆高考)已知变量x与y正相关，且由观测数据算得样本平均数＝3，＝3.5，则由该观测数据算得的线性回归方程可能为(　　)‎ A.＝0.4x＋2.3 B.＝2x－2.4‎ C.＝－2x＋9.5 D.＝－0.3x＋4.4‎ ‎2．(2013·福建高考)已知x与y之间的几组数据如下表：‎ ‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6 ‎ y ‎0‎ ‎2‎ ‎1‎ ‎3‎ ‎3‎ ‎4‎ 假设根据上表数据所得线性回归直线方程为＝x＋，若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y＝b′x＋a′，则以下结论正确的是(　　)‎ A.>b′，>a′ B.>b′，a′ D.a′.‎ ‎3．选D　由于回归直线的斜率为正值，故y与x具有正的线性相关关系，选项A中的结论正确；回归直线过样本点的中心，选项B中的结论正确；根据回归直线斜率的意义易知选项C中的结论正确；由于回归分析得出的是估计值，故选项D中的结论不正确．‎ ‎4．解：(1)由已知得，样本中有25周岁(含25周岁)以上组工人60名，25周岁以下组工人40名．‎ 所以，样本中日平均生产件数不足60件的工人中，25周岁以上组工人有60×0.05＝3(人)，记为A1，A2，A3；25周岁以下组工人有40×0.05＝2(人)，记为B1，B2.‎ 从中随机抽取2名工人，所有的可能结果共有10种，它们是：(A1，A2)，(A1，A3)，(A2，A3)，(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)．‎ 其中，至少1名“25周岁以下组”工人的可能结果共有7种，它们是(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)．故所求的概率P＝.‎ ‎(2)由频率分布直方图可知，在抽取的100名工人中，“25周岁以上组(含25周岁)”中的生产能手有60×0.25＝15(人)，“25周岁以下组”中的生产能手有40×0.375＝15(人)，据此可得2×2列联表如下：‎ 生产能手 非生产能手 合计 ‎25周岁以上组 ‎15‎ ‎45‎ ‎60‎ ‎25周岁以下组 ‎15‎ ‎25‎ ‎40‎ 合计 ‎30‎ ‎70‎ ‎100‎ 所以得K2＝ ‎＝＝≈1.79.‎ 因为1.79<2.706，‎ 所以没有90%的把握认为“生产能手与工人所在的年龄组有关”．‎