【数学】2018届一轮复习人教A版2-3函数的奇偶性与周期性学案
§2.3 函数的奇偶性与周期性
考纲展示►
1.结合具体函数,了解函数奇偶性的含义.
2.会运用函数的图象理解和研究函数的奇偶性.
3.了解函数周期性、最小正周期的含义,会判断、应用简单函数的周期性.
考点1 函数奇偶性的判断
函数的奇偶性
奇偶性
定义
图象特点
偶函数
如果对于函数f(x)的定义域内任意一个x,都有________,那么函数f(x)就叫做偶函数
关于________对称
奇函数
如果对于函数f(x)的定义域内任意一个x,都有________,那么函数f(x)就叫做奇函数
关于________对称
答案:f(-x)=f(x) y轴 f(-x)=-f(x)
原点
[教材习题改编] 函数f(x)=x3, f(x)=x4,f(x)=x2-,f(x)=+|x|中,偶函数的个数是__________.
答案:2
解析:f(x)=x4和f(x)=x2-为偶函数.
判断函数奇偶性的易错点:忽略定义域;变形错误.
(1)函数f(x)=(x+1)在定义域上是________函数.(填“奇”“偶”或“非奇非偶”)
答案:非奇非偶
解析:要使函数有意义,必须使≥0,即≤0,解得-1
1时,-x<-1,所以f(-x)=(-x)2-2=-(-x2+2)=-f(x);
当x<-1时,-x>1,所以f(-x)=-(-x)2+2=-(x2-2)=-f(x);
当|x|≤1时,f(-x)=0=-f(x).
综上可知f(x)是奇函数.
[典题1] 判断下列函数的奇偶性:
(1)f(x)=xlg(x+);
(2)f(x)=(1-x);
(3)f(x)=
(4)f(x)=.
[解] (1)∵>|x|≥0,
∴函数f(x)的定义域为R,关于原点对称,
又f(-x)=(-x)lg[-x+]
=-xlg(-x)=xlg(+x)=f(x).
即f(-x)=f(x),∴f(x)是偶函数.
(2)当且仅当≥0时函数有意义,
∴-1≤x<1,
由于定义域关于原点不对称,
∴函数f(x)是非奇非偶函数.
(3)函数的定义域为{x|x≠0},关于原点对称,
当x>0时,-x<0,f(-x)=x2-2x-1=-f(x),
当x<0时,-x>0,f(-x)=-x2-2x+1=-f(x).
∴f(-x)=-f(x),即函数是奇函数.
(4)∵⇒-2≤x≤2且x≠0,
∴函数的定义域关于原点对称.
∴f(x)==,
又f(-x)==-,
∴f(-x)=-f(x),即函数是奇函数.
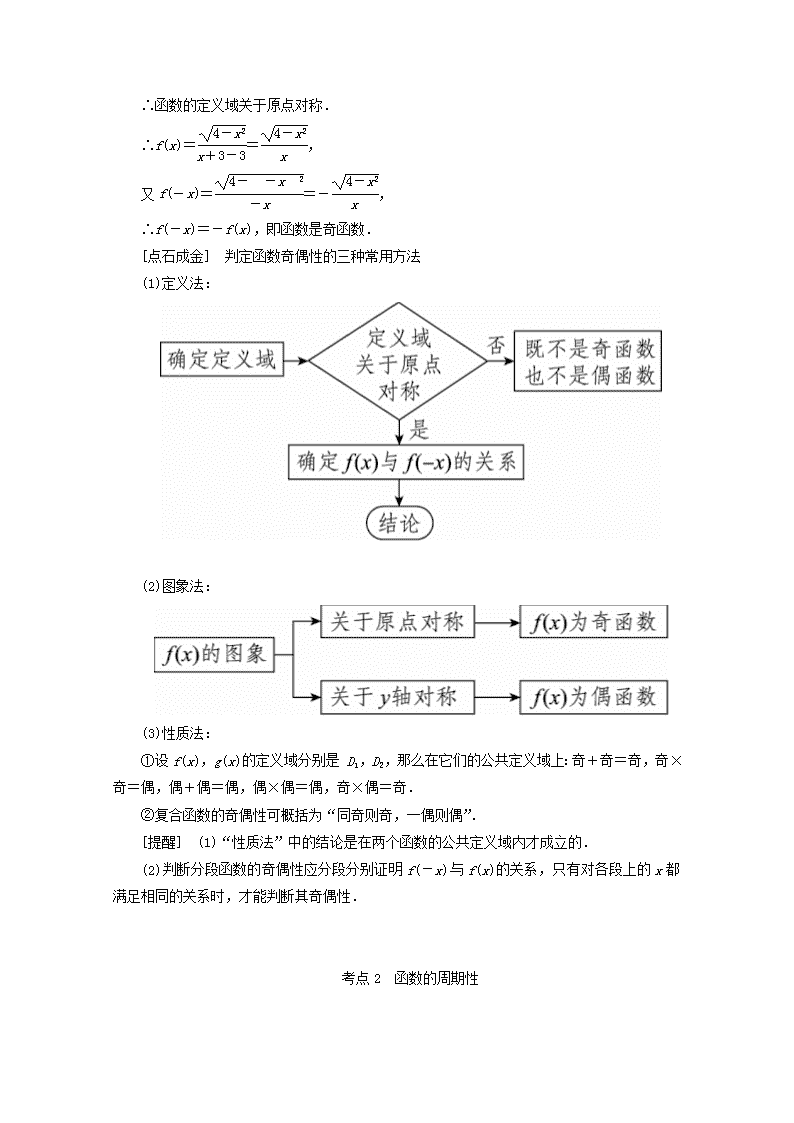
[点石成金] 判定函数奇偶性的三种常用方法
(1)定义法:
(2)图象法:
(3)性质法:
①设f(x),g(x)的定义域分别是 D1,D2,那么在它们的公共定义域上:奇+奇=奇,奇×奇=偶,偶+偶=偶,偶×偶=偶,奇×偶=奇.
②复合函数的奇偶性可概括为“同奇则奇,一偶则偶”.
[提醒] (1)“性质法”中的结论是在两个函数的公共定义域内才成立的.
(2)判断分段函数的奇偶性应分段分别证明f(-x)与f(x)的关系,只有对各段上的x都满足相同的关系时,才能判断其奇偶性.
考点2 函数的周期性
函数的周期性
(1)周期函数:
对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有________,那么就称函数y=f(x)为周期函数,称T为这个函数的周期.
(2)最小正周期:
如果在周期函数f(x)的所有周期中存在一个________的正数,那么这个________就叫做f(x)的最小正周期.
答案:(1)f(x+T)=f(x) (2)最小 最小正数
(1)[教材习题改编]已知函数f(x)满足f(x+2)=f(x),当x∈(0,1]时,f(x)=log4(x2+3),则f(2 017)=__________.
答案:1
解析:因为f(x+2)=f(x),所以f(x)是以2为周期的周期函数,所以f(2 017)=f(1 008×2+1)=f(1)=log4(12+3)=1.
(2)[教材习题改编]设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f=________.
答案:-
周期性三个常用结论.
对f(x)定义域内任一自变量的值x,最小正周期为T.
(1)若f(x+a)=-f(x),则T=__________;
(2)若f(x+a)=,则T=__________;
(3)若f(x+a)=f(x+b),则T=________.
答案:(1)2|a| (2)2|a| (3)|a-b|
解析:(1)因为f(x+2a)=f(x+a+a)
=-f(x+a)=f(x),
所以其最小正周期T=2|a|.
(2)因为f(x+2a)=f(x+a+a)
==f(x),
所以其最小正周期T=2|a|.
(3)f(x+a-b)=f[(x-b)+a]
=f[(x-b)+b]=f(x),
所以其最小正周期T=|a-b|.
[典题2] (1)[2017·山西晋中模拟]已知f(x)是R上的奇函数,f(1)=2,且对任意x∈R都有f(x+6)=f(x)+f(3)成立,则f(2 017)=________.
[答案] 2
[解析] ∵f(x)是R上的奇函数,∴f(0)=0,
又对任意x∈R都有f(x+6)=f(x)+f(3),
∴当x=-3时,有f(3)=f(-3)+f(3)=0,
∴f(-3)=0,f(3)=0,
∴f(x+6)=f(x),周期为6.
故f(2 017)=f(1)=2.
(2)设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2.
①求函数的最小正周期;
②计算f(0)+f(1)+f(2)+…+f(2 015).
[解] ①∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x).
∴f(x)的最小正周期为4.
②f(0)=0,f(1)=1,f(2)=0,
f(3)=f(-1)=-f(1)=-1.
又∵f(x)是周期为4的周期函数,
∴f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)=…=f(2 012)+f(2 013)+f(2 014)+f(2 015)=0,
∴f(0)+f(1)+f(2)+…+f(2 015)=0.
[题点发散1] 若本例(2)中条件变为“f(x+2)=-”,求函数f(x)的最小正周期.
解:∵对任意x∈R,都有f(x+2)=-,
∴f(x+4)=f(x+2+2)=-=-=f(x),∴f(x)的最小正周期为4.
[题点发散2] 若本例(2)中条件改为:定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2)2;当-1≤x<3时,f(x)=x.求f(1)+f(2)+f(3)+…+f(2 015)的值.
解:∵f(x+6)=f(x),∴T=6.
∵当-3≤x<-1时,f(x)=-(x+2)2;
当-1≤x<3时,f(x)=x.
∴f(1)=1,f(2)=2,f(3)=f(-3)=-1,
f(4)=f(-2)=0,f(5)=f(-1)=-1,
f(6)=f(0)=0,
∴f(1)+f(2)+…+f(6)=1,
∴f(1)+f(2)+…+f(6)=f(7)+f(8)+…+f(12)=…=f(2 005)+f(2 006)+…+f(2 010)=1,
∴f(1)+f(2)+…+f(2 010)=1×=335.
而f(2 011)+f(2 012)+f(2 013)+f(2 014)+f(2 015)=f(1)+f(2)+f(3)+f(4)+f(5)=1+2-1+0-1=1.
∴f(1)+f(2)+…+f(2 015)=335+1=336.
[题点发散3] 在本例(2)条件下,求f(x)(x∈[2,4])的解析式.
解:当x∈[-2,0]时,-x∈[0,2],
由已知得f(-x)=2×(-x)-(-x)2=-2x-x2,
又f(x)是奇函数,
∴f(-x)=-f(x)=-2x-x2.
∴f(x)=x2+2x.
又当x∈[2,4]时,x-4∈[-2,0],
∴f(x-4)=(x-4)2+2(x-4).
又f(x)是周期为4的周期函数,
∴f(x)=f(x-4)=(x-4)2+2(x-4)=x2-6x+8.
故x∈[2,4]时,f(x)=x2-6x+8.
[点石成金] 1.判断函数周期性的两种方法
(1)定义法.(2)图象法.
2.判断函数周期性的三个常用结论
若对于函数f(x)定义域内的任意一个x都有:
(1)f(x+a)=-f(x)(a≠0),则函数f(x)必为周期函数,2a是它的一个周期.
(2)f(x+a)=(a≠0),则函数f(x)必为周期函数,2a是它的一个周期.
(3)f(x+a)=-(a≠0),则函数f(x)必为周期函数,2a是它的一个周期.
3.函数周期性的重要应用
利用函数的周期性,可将其他区间上的求值、求零点个数、求解析式等问题,转化为已知区间上的相应问题,进而求解.
1.已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,6]上与x轴的交点的个数为( )
A.6 B.7
C.8 D.9
答案:B
解析:∵f(x)是最小正周期为2的周期函数,且0≤x<2时,f(x)=x3-x=x(x-1)(x+1),
∴当0≤x<2时,f(x)=0有两个根,即x1=0,x2=1.
由周期函数的性质知,当2≤x<4时,f(x)=0有两个根,即x3=2,x4=3;
当4≤x≤6时,f(x)=0有两个根,即x5=4,x6=5,x7=6也是f(x)=0的根.
故函数f(x)的图象在区间[0,6]上与x轴交点的个数为7.
2.[2017·广东广州模拟]已知f(x)是定义在R上的偶函数,且f(x+2)=-f(x),当2≤x≤3时,f(x)=x,则f(105.5)=________.
答案:2.5
解析:由f(x+2)=-f(x),得f(x+4)=f((x+2)+2)=-f(x+2)=-[-f(x)]=f(x),所以函数f(x)的周期为4,所以f(105.5)=f(4×27-2.5)=f(-2.5)=f(2.5)=2.5.
考点3 函数性质的综合应用
(1)[教材习题改编]若f(x)是偶函数且在(0,+∞)上为增函数,则函数f(x)在(-∞,0)上为________.
答案:减函数
(2)[教材习题改编]设函数f(x)是定义在R上的奇函数,若当x∈(0,+∞)时,f(x)=lg x,则满足f(x)>0的x的取值范围是________.
答案:(-1,0)∪(1,+∞)
[考情聚焦] 高考常将函数的单调性、奇偶性及周期性相结合来命题,以选择题或填空题的形式考查,难度稍大,为中高档题.
主要有以下几个命题角度:
角度一
奇偶性的应用
[典题3] (1)[2017·河北武邑中学高三上期中]已知f(x)满足对∀x∈R,f(-x)+f(x)=0,且x≥0时,f(x)=ex+m(m为常数),则f(-ln 5)的值为( )
A.4 B.-4
C.6 D.-6
[答案] B
[解析] 由题设函数f(x)是奇函数,故f(0)=e0+m=1+m=0,即m=-1,所以f(-ln 5)=-f(ln 5)=-eln 5+1=-5+1=-4,故选B.
(2)设函数f(x)=为奇函数,则a=________.
[答案] -1
[解析] ∵f(x)=为奇函数,
∴f(1)+f(-1)=0,
即+=0,
∴a=-1.
角度二
函数的奇偶性与单调性相结合问题
[典题4] (1)设偶函数f(x)的定义域为R,当x∈[0,+∞)时f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是( )
A.f(π)>f(-3)>f(-2)
B.f(π)>f(-2)>f(-3)
C.f(π)<f(-3)<f(-2)
D.f(π)<f(-2)<f(-3)
[答案] A
[解析] 因为π>3>2,且当x∈[0,+∞)时f(x)是增函数,所以f(π)>f(3)>f(2).
又函数f(x)为R上的偶函数,
所以f(-3)=f(3),f(-2)=f(2),
故f(π)>f(-3)>f(-2).
(2)已知函数f(x)是定义域为R的偶函数,且在区间[0,+∞)上是增函数,若f(m)≥f(-2),则实数m的取值范围是________.
[答案] (-∞,-2]∪[2,+∞)
[解析] 函数f(x)是R上的偶函数,且在[0,+∞)上是增函数,
所以f(x)在(-∞,0]上是减函数.
当m<0时,由f(m)≥f(-2),知m≤-2;
当m≥0时,由f(m)≥f(-2),f(-2)=f(2)可得,f(m)≥f(2),所以m≥2.
故实数m的取值范围是(-∞,-2]∪[2,+∞).
角度三
函数的周期性与奇偶性相结合问题
[典题5] (1)已知f(x)是定义在R上的以3为周期的偶函数,若f(1)<1,f(5)=,则实数a的取值范围为( )
A.(-1,4) B.(-2,0)
C.(-1,0) D.(-1,2)
[答案] A
[解析] ∵f(x)是定义在R上的周期为3的偶函数,∴f(5)=f(5-6)=f(-1)=f(1),
∵f(1)<1,f(5)=,
∴<1,即<0,
解得-1<a<4.
(2)若函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)= 则f+f=________.
[答案]
[解析] 由于函数f(x)是周期为4的奇函数,
所以f+f=f+f
=f+f=-f-f
=-+sin =.
角度四
函数的单调性、奇偶性与周期性相结合问题
[典题6] (1)已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则( )
A.f(-25)0)
5.对称性的三个常用结论
(1)若函数y=f(x+a)是偶函数,即f(a-x)=f(a+x),则函数y=f(x)的图象关于直线x=a对称.
(2)若对于R上的任意x都有f(2a-x)=f(x)或f(-x)=f(2a+x),则y=f(x)的图象关于直线x=a对称.
(3)若函数y=f(x+b)是奇函数,即f(-x+b)+f(x+b)=0,则函数y=f(x)关于点(b,0)中心对称.
[易错防范] 1.f(0)=0既不是f(x)是奇函数的充分条件,也不是必要条件.
2.分段函数奇偶性判定时,要以整体的观点进行判断,不可以利用函数在定义域某一区间上不是奇偶函数而否定函数在整个定义域的奇偶性.
真题演练集训
1.[2015·福建卷]下列函数为奇函数的是( )
A.y= B.y=|sin x|
C.y=cos x D.y=ex-e-x
答案:D
解析:对于D,f(x)=ex-e-x的定义域为R,f(-x)=e-x-ex=-f(x),故y=ex-e-x为奇函数.而y=的定义域为{x|x≥0},不具有对称性,故y=为非奇非偶函数.y=|sin x|和y=cos x为偶函数.
2.[2014·新课标全国卷Ⅰ]设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.f(x)g(x)是偶函数
B.|f(x)|g(x)是奇函数
C.f(x)|g(x)|是奇函数
D.|f(x)g(x)|是奇函数
答案:C
解析:A:令h(x)=f(x)g(x),
则h(-x)=f(-x)·g(-x)=-f(x)g(x)=-h(x),
∴h(x)是奇函数,A错.
B:令h(x)=|f(x)|g(x),则h(-x)=|f(-x)|·g(-x)=|-f(x)|g(x)=|f(x)|g(x)=h(x),
∴h(x)是偶函数,B错.
C:令h(x)=f(x)|g(x)|,则h(-x)=f(-x)|g(-x)|=-f(x)|g(x)|,∴h(x)是奇函数,C正确.
D:令h(x)=|f(x)g(x)|,则h(-x)=|f(-x)g(-x)|=|-f(x)g(x)|=|f(x)g(x)|=h(x),∴h(x)是偶函数,D错.
3.[2016·山东卷]已知函数f(x)的定义域为R.当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=-f(x);当x>时,f=f,则f(6)=( )
A.-2 B.-1
C.0 D.2
答案:D
解析:由题意可知,当-1≤x≤1时,f(x)为奇函数,且当x>时,f(x+1)=f(x),所以f(6)=f(5×1+1)=f(1).而f(1)=-f(-1)=-[(-1)3-1]=2,所以f(6)=2.故选D.
4.[2015·新课标全国卷Ⅰ]若函数f(x)=xln(x+)为偶函数,则a=________.
答案:1
解析:∵ f(x)为偶函数,∴ f(-x)-f(x)=0恒成立,∴ -xln(-x+)-xln(x+)=0恒成立,∴ xln a=0恒成立,
∴ ln a=0,即a=1.
5.[2016·四川卷]已知函数f(x)是定义在R上的周期为2的奇函数,当00,f(x+2)=,对任意x∈R恒成立,则f(2 015)=( )
A.4 B.3
C.2 D.1
[思路分析]
[解析] 因为f(x)>0,f(x+2)=,
所以f(x+4)=f((x+2)+2)
===f(x),
即函数f(x)的周期是4.
所以f(2 015)=f(504×4-1)=f(-1),
因为函数f(x)为偶函数,
所以f(2 015)=f(-1)=f(1).
当x=-1时,f(-1+2)=,得
f(1)=.
即f(1)=1,所以f(2 015)=f(1)=1.
[答案] D
方法探究
对于抽象函数,常常利用恰当赋值解答问题,在赋值时要注意观察变量与所求问题之间的关系,有时需要进行多次赋值.
3.抽象函数的奇偶性
抽象函数的奇偶性就是要判断-x对应的函数值与x对应的函数值之间的关系,从而得到函数图象关于原点或y轴对称,再结合函数的图象作出进一步的判断.
[典例3] 已知函数f(x)对任意x,y∈R,都有f(x+y)+f(x-y)=2f(x)f(y),且f(0)≠0,求证:f(x)是偶函数.
[思路分析]
[证明] 已知对任意x,y∈R,都有f(x+y)+f(x-y)=2f(x)f(y),
不妨取x=0,y=0,则有2f(0)=2[f(0)]2,
因为f(0)≠0,所以f(0)=1.
取x=0,得f(y)+f(-y)=2f(0)f(y)=2f(y),
所以f(y)=f(-y).
又y∈R,所以函数f(x)是偶函数.
方法探究
在利用函数奇偶性的定义进行判断时,如果等式中还有其他的量未解决,例如本题中的f(0),就需要令x,y取特殊值进行求解.
4.抽象函数的单调性与抽象不等式
抽象函数的单调性一直是高考考查的难点,常出现在一些综合性问题中,需要先对所含的参数进行分类讨论或根据已知条件确定出参数的范围,再根据单调性求解或证明抽象不等式.
[典例4] 设函数f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y).若f(3)=1,且f(a)>f(a-1)+2,求实数a的取值范围.
[思路分析]
[解] 因为f(xy)=f(x)+f(y),且f(3)=1,
所以2=2f(3)=f(3)+f(3)=f(9).
又f(a)>f(a-1)+2,所以f(a)>f(a-1)+f(9).
再由f(xy)=f(x)+f(y),可知f(a)>f(9(a-1)).
因为f(x)是定义在(0,+∞)上的增函数,
从而有解得19(a-1).