2021届课标版高考文科数学大一轮复习课件：§5-1 平面向量的概念及线性运算、平面向量的基本定理（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§5-1 平面向量的概念及线性运算、平面向量的基本定理（讲解部分）

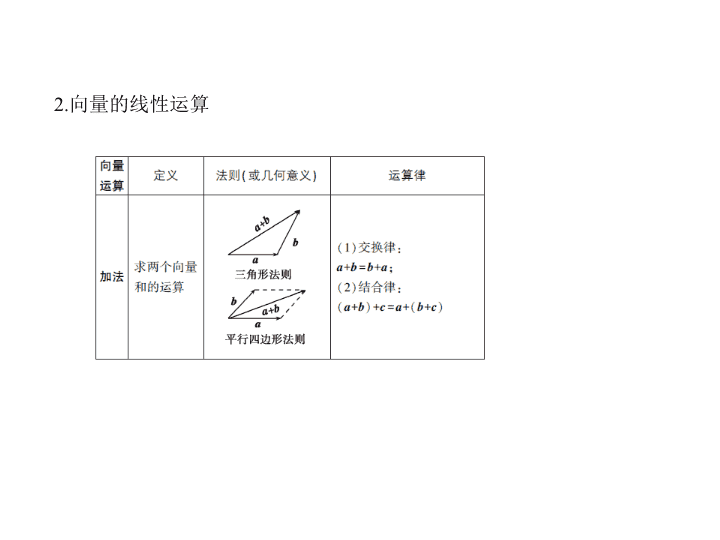
考点一    平面向量的线性运算及其几何意义 考点清单 考向基础 1.向量的有关概念及表示法 2.向量的线性运算 3.向量共线定理 向量 b 与非零向量 a 共线的充要条件为 存在唯一实数 λ ,使得 b = λa 成立. 【知识拓展】 1.若   +   =2   ,则 D 为线段 BC 的中点,反之也成立. 2.| a + b | 2 +| a - b | 2 =2(| a | 2 +| b | 2 ). 3.若 O 为原点, A , B , C 为平面内三点,则 A , B , C 三点在一条直线上的充要条件 是   = α   + β   ,且 α + β =1, α , β ∈R . 考向突破 考向一　平面向量的线性运算 例1    (2020届河南顶级名校摸底,5)在如图所示的△ ABC 中,点 D , E 分别在 BC , AD 上,且 BD = DC , ED =2 AE ,则向量   =   (　　)   A.     +     　    B.     +     C.     +     　    D.     +     解析　∵   =   +   ,   =   +   ,又∵ BD = DC ,∴   =-   ,∴   =   (   +   ),又∵ ED =2 AE ,∴   =     ,∴   =     =     +     ,故选B. 答案    B 考向二　向量共线定理的应用 例2    (2020届湖南永州9月摸底,6)如图,在△ ABC 中,   =     , P 是 BN 上一 点,若   = m   +     ,则实数 m 的值为(　　)   A.   　    B.   　    C.   　    D.   解析　由题意可得   =5   ,则   = m   +   × 5   = m   +     ,因为 B , N , P 三点共线,所以 m +   =1,即 m =   ,故选D. 答案    D 考点二    平面向量基本定理及向量的坐标运算 考向基础 1.平面向量基本定理 如果 e 1 , e 2 是同一平面内的两个 不共线 向量,那么对于这一平面内的任意向 量 a , 有且只有 一对实数 λ 1 , λ 2 ,使 a = λ 1 e 1 + λ 2 e 2 . 其中,不共线的向量 e 1 , e 2 叫做表示这一平面内所有向量的一组基底. 温馨提示　(1)零向量和共线向量不能作基底; (2)基底给定,同一向量的分解形式唯一 ; (3)若 λ 1 e 1 + λ 2 e 2 =0,则 λ 1 = λ 2 =0. 2.平面向量的坐标运算 (1)加法、减法、数乘运算 (2)向量坐标的求法 已知 A ( x 1 , y 1 ), B ( x 2 , y 2 ),则   =( x 2 - x 1 , y 2 - y 1 ),即一个向量的坐标等于表示该向量 的有向线段的终点的坐标减去始点的坐标. (3)平面向量共线的坐标表示 设 a =( x 1 , y 1 ), b =( x 2 , y 2 ),其中 b ≠ 0,则 a 与 b 共线 ⇔ a = λb ⇔ x 1 y 2 - x 2 y 1 =0 . 向量 a b a + b a - b λa 坐标 ( x 1 , y 1 ) ( x 2 , y 2 ) ( x 1 + x 2 , y 1 + y 2 ) ( x 1 - x 2 , y 1 - y 2 ) ( λx 1 , λy 1 ) 考向突破 考向一　平面向量基本定理的应用 例3    (2019山东烟台调研,14)在△ ABC 中,点 M , N 满足   =2   ,   =   ,若   = x   + y   ,则 x + y = 　　　     . 解析       =   +   =     +     =     +   (   -   )=     -     , 又   = x   + y   ,所以 x =   , y =-   , 故 x + y =   -   =   . 答案       考向二　平面向量共线的坐标表示及运算 例4    (2019云南师范大学附属中学,贵阳一中,南宁三中高三联考,8)若 a =( k , 1), b =(3,2),且 a , b 共线,则( a - b )·(2 a + b )=   (　　) A.-13　    B.0　    C.-12　    D.-5 解析　∵ a , b 共线,∴3=2 k ,∴ k =   ,∴ a =   , 又 b =(3,2),则 a - b =   ,2 a + b =(6,4), ∴( a - b )·(2 a + b )=-9+(-4)=-13,故选A. 答案    A 方法1 　向量共线问题的求解方法 1.两非零向量共线是指存在实数 λ 使两向量可以互相表示. 2.向量共线的充要条件中要注意当两向量共线时,通常只有非零向量才能 表示与之共线的其他向量,要注意待定系数法和方程思想的运用. 3.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线 的区别与联系,当两向量共线且有公共点时,才能得到三点共线. 4. A 、 B 、 C 三点共线 ⇔   = λ   + μ   且 λ + μ =1.特别地,当 λ = μ =   时, C 为线 段 AB 的中点. 5.若 a =( x 1 , y 1 ), b =( x 2 , y 2 ),则 a ∥ b ⇔ x 1 y 2 - x 2 y 1 =0. 方法技巧 例1    (2018课标全国Ⅲ,13,5分)已知向量 a =(1,2), b =(2,-2), c =(1, λ ).若 c ∥(2 a + b ),则 λ = 　　　     . 解析　由题意得2 a + b =(4,2),因为 c =(1, λ ), c ∥(2 a + b ),所以4 λ -2=0,解得 λ =   . 答案       例2　如图所示,在△ ABC 中,点 O 是 BC 的中点,过点 O 的直线分别交直线 AB 、 AC 于不同的两点 M 、 N ,若   = m   ,   = n   ,则 m + n 的值为 　　          .   解析　解法一:连接 AO ,由于 O 为 BC 的中点, 故   =   (   +   ).   =   -   =   (   +   )-     =     +     , 同理,   =     +     . 由于向量   ,   共线, 故存在实数 λ ,使得   = λ   , 即     +     = λ   , 由于   ,   不共线, 故得   -   =   λ 且   = λ   , 消去 λ ,得( m -2)( n -2)= mn , 化简即得 m + n =2. 解法二:连接 AO ,∵ O 是 BC 的中点, ∴   =   (   +   ). 又∵   = m   ,   = n   , ∴   =     +     . ∵ M 、 O 、 N 三点共线, ∴   +   =1.∴ m + n =2. 答案　2 方法2　 利用平面向量基本定理解决问题的方法 用平面向量基本定理解决问题的一般思路是先选择一组基底,并运用平面 向量基本定理将条件和结论表示成基底的线性组合,再通过向量的运算来 求解.在基底未给出的情况下,合理地选取基底会给解题带来方便.另外,要 熟练运用线段中点的向量表达式. 例3    (2019豫南九校第三次联考,8)如图所示,在△ ABC 中,点 M 是 AB 的中 点,且   =     , BN 与 CM 相交于点 E ,设   = a ,   = b ,则   等于   (　　)   A.   a +   b 　　B.   a +   b C.   a +   b 　　D.   a +   b   解析　由题意得   =     =   b ,   =     =   a , 由 N , E , B 三点共线可知,存在实数 m ,使   = m   +(1- m )·   =   mb +(1- m ) a . 由 C , E , M 三点共线可知,存在实数 n ,使   = n   +(1- n )·   =   na +(1- n ) b , 所以   mb +(1- m ) a =   na +(1- n ) b , 因为 a , b 为基底,所以   解得   所以   =   a +   b ,故选A. 答案    A