直线、平面平行的判定及其性质教案1

直线、平面平行的判定及其性质教案1

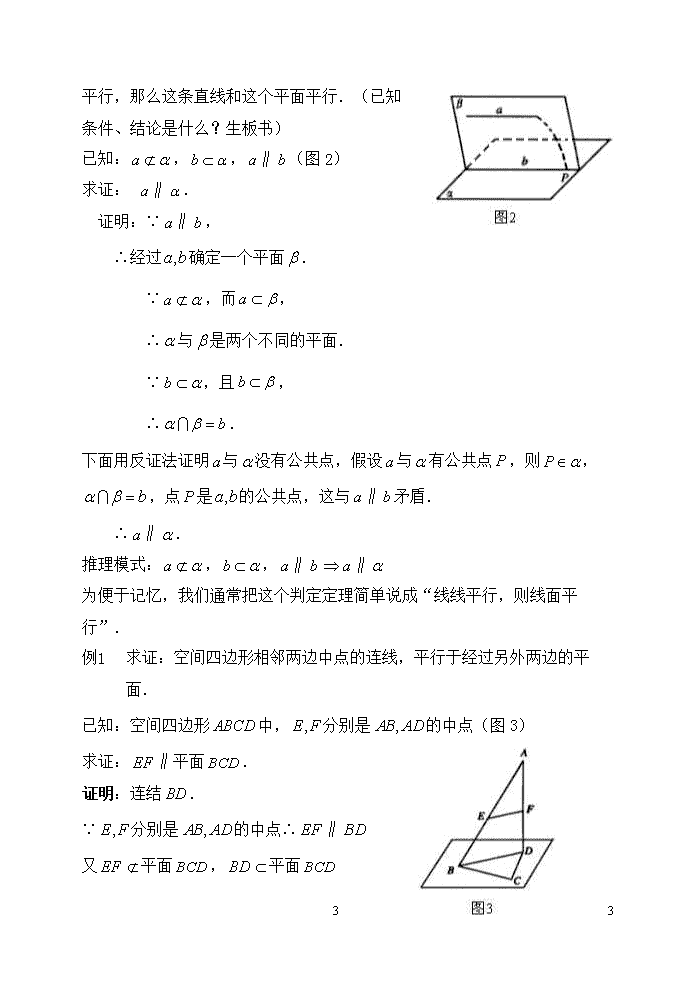
‎ ‎ 课 题  直线与平面平行的判定和性质 （1）‎ 教学目标 ‎1．理解并掌握直线和平面平行的定义．‎ ‎2．了解直线和平面的三种位置关系，体现了分类的思想．‎ ‎3．通过对比的方法，使学生掌握直线和平面的各种位置关系的图形的画法，进一步培养学生的空间想象能力．‎ ‎4．掌握直线和平面平行的判定定理的证明，证明用的是反证法和空间直线与平面的位置关系，进一步培养学生严格的逻辑思维。除此之外，还要会灵活运用直线和平面的判定定理，把线面平行转化为线线平行．‎ 教学重点：直线与平面的位置关系；直线与平面平行的判定定理．‎ 教学难点：掌握直线与平面平行的判定定理的证明及应用．‎ 教学疑点：除直线在平面内的情形外，空间的直线和平面，不平行就相交，课本中用记号aα统一表示a∥α，a∩α=A两种情形，统称直线a在平面α外．‎ 教学方法：讲解法 讨论法 课时安排：1课时 教 具：投影仪（胶片）、三角板、自制模型等 教学过程 设置情境：空间两直线有三种位置关系：平行、相交与异面．直线和平面有哪几种位置关系？我们来观察：黑板上的一条直线在黑板面内；两墙面的相交线和地面只相交于一点；墙面和天花板的相交线和地面没有公共点，等等．如果把这些实物作出抽象，如把“墙面”、“天花板”等想象成“水平的平面”，把“相交线”等想象成“水平的直线”，那么上面这些关系其实就是直线和平面的位置关系，有几种，分别是什么？‎ 探索研究：1.直线和平面的位置关系 生：直线和平面的位置关系有三种：‎ 4‎ 4‎ ‎ ‎ 直线在平面内——有无数个公共点．‎ ‎2.线面位置关系的画法 师：如何画出表示直线和平面的三种位置关系的图形呢？（生讨论并回答）‎ 生：直线a在平面α内，应把直线a画在表示平面α的平行四边形内，直线不要超出表示平面的平行四边形的各条边；直线a与平面α相交，交点到水平线这一段是不可见的，注意画成虚线或不画；直线a与平面α平行，直线要与表示平面的平行四边形的一组对边平行． ‎ ‎ ‎ ‎ ‎ 练习：P ‎3.直线和平面平行的判定定理 师：什么是直线和平面平行？‎ 生：如果一条直线和一个平面没有公共点，那么这条直线和这个平面平行．‎ 直线与平面是否平行，可以直接用定义来检验，但“没有公共点”不好验证，所以我们来寻找比较实用又便于验证的判定定理．我们先来观察：门框的对边是平行的，如图a∥b，当门扇绕着一边a转动时，另一边b始终与门扇不会有公共点，即b平行于门扇．由此我们得到：‎ 直线和平面平行的判定定理 ‎ 4‎ 4‎ ‎ ‎ ‎ 如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行．（已知条件、结论是什么？生板书）‎ 已知：，，∥（图2）‎ 求证： ∥．‎ ‎　证明：∵∥，‎ ‎∴经过确定一个平面．‎ ‎　　∵，而，‎ ‎　　∴与是两个不同的平面． ‎ ‎　　∵，且，‎ ‎　　∴．‎ 下面用反证法证明与没有公共点，假设与有公共点，则，，点是的公共点，这与∥矛盾．‎ ‎∴∥．‎ 推理模式：，，∥∥　　‎ 为便于记忆，我们通常把这个判定定理简单说成“线线平行，则线面平行”．‎ 例1 求证：空间四边形相邻两边中点的连线，平行于经过另外两边的平面．　　‎ 已知：空间四边形中，分别是的中点（图3）‎ 求证：∥平面．‎ 证明：连结．‎ ‎∵分别是的中点∴∥‎ 又平面，平面 4‎ 4‎ ‎ ‎ ‎∴∥平面.‎ 演练反馈 ‎1．课本P19练习1至3‎ ‎2．课本P19习题9.3   1和2‎ ‎2．提示：设书脊所在直线为，桌面所在平面为，则或，∵，．‎ ‎3．提示：      同理．‎ ‎4．提示：在面内过点作即可．‎ ‎5．提示：错、错、错、对．‎ 总结提炼 ‎　　利用线面平行的判定与性质定理必须记清条件，它们各有三个条件．‎ ‎　　判定定理： ，，∥∥‎ 布置作业：习题9.3  1、3、4‎ 板书设计：9.3  直线与平面平行的判定和性质 （1）‎ ‎1．线面位置关系          例1 ‎ ‎2．判定定理               ‎ 课后反思：‎ 4‎ 4‎