2014高考山东（文科数学）试卷

2014高考山东（文科数学）试卷

‎2014·山东卷(文科数学)‎ ‎1．[2014·山东卷] 已知a，b∈R，i是虚数单位，若a＋i＝2－bi，则(a＋bi)2＝(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．3－4iB．3＋4i C．4－3iD．4＋3i ‎1．A　[解析]因为a＋i＝2－bi，所以a＝2，b＝－1，所以(a＋bi)2＝(2－i)2＝3－4i.‎ ‎2．[2014·山东卷] 设集合A＝{x|x2－2x<0}，B＝{x|1≤x≤4}，则A∩B＝(　　)‎ A．(0，2] B．(1，2)‎ C．[1，2) D．(1，4)‎ ‎2．C　[解析]因为集合A＝{x|0＜x＜2}，B＝{x|1≤x≤4}，所以A∩B＝{x|1≤x＜2}，故选C.‎ ‎3．[2014·山东卷] 函数f(x)＝的定义域为(　　)‎ A．(0，2) B．(0，2] ‎ C．(2，＋∞) D．[2，＋∞)‎ ‎3．C　[解析]若函数f(x)有意义，则log2x－1＞0，∴log2x＞1，∴x＞2.‎ ‎4．[2014·山东卷] 用反证法证明命题“设a，b为实数，则方程x2＋ax＋b＝0至少有一个实根”时，要做的假设是(　　)‎ A．方程x2＋ax＋b＝0没有实根 B．方程x2＋ax＋b＝0至多有一个实根 C．方程x2＋ax＋b＝0至多有两个实根 D．方程x2＋ax＋b＝0恰好有两个实根 ‎4．A　[解析]方程“x2＋ax＋b＝0至少有一个实根”等价于“方程x2＋ax＋b＝0有一个实根或两个实根”，所以该命题的否定是“方程x2＋ax＋b＝0没有实根”．故选A.‎ ‎5．，[2014·山东卷] 已知实数x，y满足axy3‎ B．sinx>siny C．ln(x2＋1)>ln(y2＋1) ‎ D.> ‎5．A　[解析]因为ax＜ay(0＜a＜1)，所以x＞y，所以x3>y3恒成立．故选A.‎ ‎6．，[2014·山东卷] 已知函数y＝loga(x＋c)(a，c为常数，其中a>0，a≠1)的图像如图11所示，则下列结论成立的是(　　)‎ 图11‎ 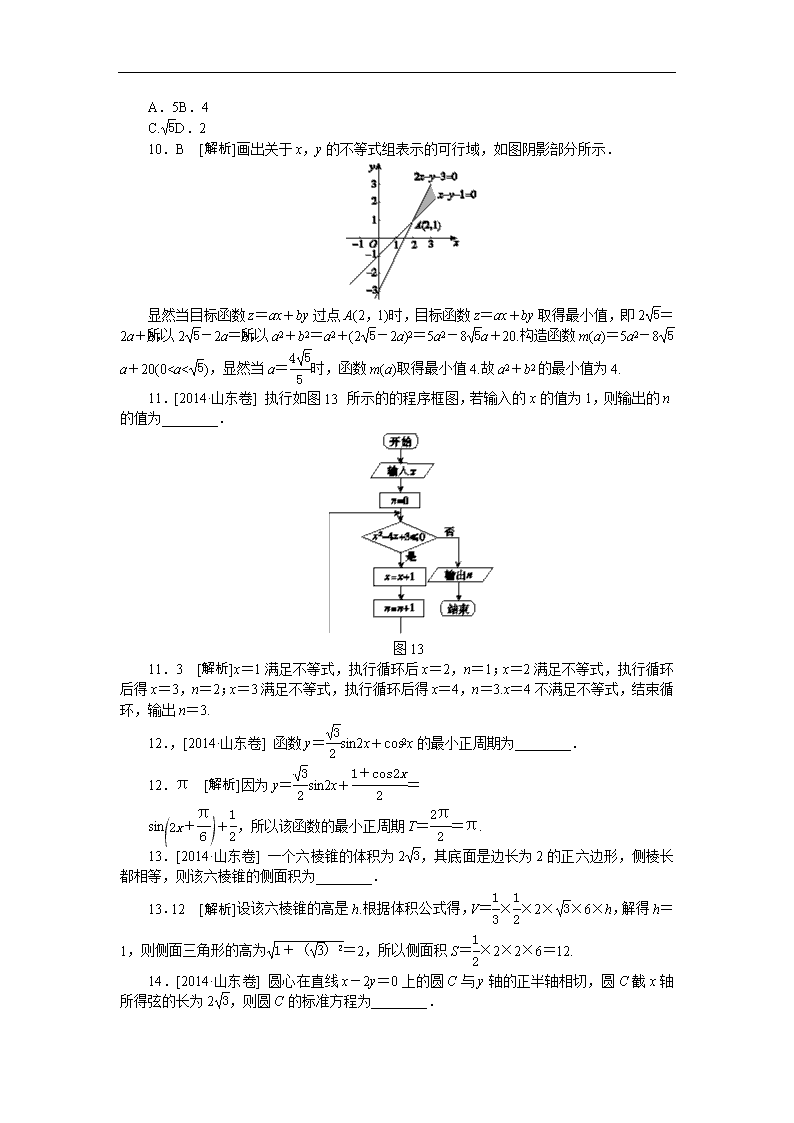A．a>1，x>1B．a>1，01D．00，b>0)在该约束条件下取到最小值2时，a2＋b2的最小值为(　　)‎ A．5B．4‎ C.D．2‎ ‎10．B　[解析]画出关于x，y的不等式组表示的可行域，如图阴影部分所示．‎ 显然当目标函数z＝ax＋by过点A(2，1)时，目标函数z＝ax＋by取得最小值，即2＝2a＋b，所以2－2a＝b，所以a2＋b2＝a2＋(2－2a)2＝5a2－8a＋20.构造函数m(a)＝5a2－8a＋20(00，圆的半径是2b.由勾股定理可得b2＋()2＝4b2，解得b＝±1.又因为b>0，所以b＝1，所以圆C的圆心坐标为(2，1)，半径是2，所以圆C的标准方程是(x－2)2＋(y－1)2＝4.‎ ‎15．，[2014·山东卷] 已知双曲线－＝1(a>0，b>0)的焦距为2c，右顶点为A，抛物线x2＝2py(p>0)的焦点为F.若双曲线截抛物线的准线所得线段长为2c，且|FA|＝c，则双曲线的渐近线方程为________．‎ ‎15．y＝±x　[解析]由题意可知，抛物线的焦点F为，准线方程为y＝－.因为|FA|＝c，所以＋a2＝c2，即＝b2.联立消去y，得x＝±，即x＝±a.又因为双曲线截抛物线的准线所得的线段长为2c，所以2a＝2c，即a＝c，所以b＝a，所以双曲线的渐近线方程为y＝±x.‎ ‎16．，[2014·山东卷] 海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量(单位：件)如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．‎ 地区 A B C 数量 ‎50‎ ‎150‎ ‎100‎ ‎(1)求这6件样品中来自A，B，C各地区商品的数量；‎ ‎(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．‎ ‎16．解：(1)因为样本容量与总体中的个体数的比是 ＝，所以样本中包含三个地区的个体数量分别是：50×＝1，150×＝3，100×＝2.‎ 所以A，B，C三个地区的商品被选取的件数分别是1，3，2.‎ ‎(2)设6件来自A，B，C三个地区的样品分别为：A；B1，B2，B3；C1，C2.则抽取的这2件商品构成的所有基本事件为：‎ ‎{A，B1}，{A，B2}，{A，B3}，{A，C1}，{A，C2}，{B1，B2}，{B1，B3}，{B1，C1}，{B1，C2}，{B2，B3}{B2，C1}，{B2，C2}，{B3，C1}，{B3，C2}，{C1，C2}，共15个．‎ 每个样品被抽到的机会均等，因此这些基本事件的出现是等可能的．‎ 记事件D为“抽取的这2件商品来自相同地区”，‎ 则事件D包含的基本事件有{B1，B2}，{B1，B3}，{B2，B3}，{C1，C2}，共4个．‎ 所以P(D)＝，即这2件商品来自相同地区的概率为.‎ ‎17．，，[2014·山东卷] △ABC中，角A，B，C所对的边分别为a，b，c.已知a＝3，cosA＝，B＝A＋.‎ ‎(1)求b的值；‎ ‎(2)求△ABC的面积．‎ ‎17．解：(1)在△ABC中，‎ 由题意知，sinA＝＝.‎ 又因为B＝A＋，‎ 所以sinB＝sin＝cosA＝.‎ 由正弦定理可得，b＝＝＝3.‎ ‎(2)由B＝A＋得cosB＝cos＝－sinA＝－.‎ 由A＋B＋C＝π，得C＝π－(A＋B)，‎ 所以sinC＝sin[π－(A＋B)]‎ ‎＝sin(A＋B)‎ ‎＝sinAcosB＋cosAsinB ‎＝×＋× ‎＝.‎ 因此△ABC的面积S＝absinC＝×3×3×＝.‎ ‎18．，[2014·山东卷] 如图14所示，四棱锥PABCD中，AP⊥平面PCD，AD∥BC，AB＝BC＝AD，E，F分别为线段AD，PC的中点．‎ 图14‎ ‎(1)求证：AP∥平面BEF；‎ ‎(2)求证：BE⊥平面PAC.‎ ‎18．证明：(1)设AC∩BE＝O，连接OF，EC.由于E为AD的中点，‎ AB＝BC＝AD，AD∥BC，‎ 所以AE∥BC，AE＝AB＝BC，‎ 所以O为AC的中点．‎ 又在△PAC中，F为PC的中点，所以AP∥OF.‎ 又OF⊂平面BEF，AP⊄平面BEF，‎ 所以AP∥平面BEF.‎ ‎(2)由题意知，ED∥BC，ED＝BC，‎ 所以四边形BCDE为平行四边形，‎ 所以BE∥CD.‎ 又AP⊥平面PCD，‎ 所以AP⊥CD，所以AP⊥BE.‎ 因为四边形ABCE为菱形，‎ 所以BE⊥AC.‎ 又AP∩AC＝A，AP，AC⊂平面PAC，‎ 所以BE⊥平面PAC.‎ ‎19．，，[2014·山东卷] 在等差数列{an}中，已知公差d＝2，a2是a1与a4的等比中项．‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设bn＝a，记Tm＝－b1＋b2－b3＋b4－…＋(－1)nbn，求Tn.‎ ‎19．解：(1)由题意知，(a1＋d)2＝a1(a1＋3d)，‎ 即(a1＋2)2＝a1(a1＋6)，解得a1＝2.‎ 故数列{an}的通项公式为an＝2n.‎ ‎(2)由题意知，bn＝a＝n(n＋1)，‎ 所以Tn＝－1×2＋2×3－3×4＋…＋(－1)nn×(n＋1)．‎ 因为bn＋1－bn＝2(n＋1)，‎ 所以当n为偶数时，‎ Tn＝(－b1＋b2)＋(－b3＋b4)＋…＋(－bn－1＋bn)‎ ‎＝4＋8＋12＋…＋2n ‎＝ ‎＝，‎ 当n为奇数时，‎ Tn＝Tn－1＋(－bn)‎ ‎＝－n(n＋1)‎ ‎＝－.‎ 所以Tn＝ ‎20．，[2014·山东卷] 设函数f(x)＝alnx＋，其中a为常数．‎ ‎(1)若a＝0，求曲线y＝f(x)在点(1，f(1))处的切线方程；‎ ‎(2)讨论函数f(x)的单调性．‎ ‎20．解：(1)由题意知，当a＝0时，f(x)＝，x∈(0，＋∞)．‎ 此时f′(x)＝，所以f′(1)＝.‎ 又f(1)＝0，所以曲线y＝f(x)在(1，f(1))处的切线方程为x－2y－1＝0.‎ ‎(2)函数f(x)的定义域为(0，＋∞)．‎ f′(x)＝＋＝.‎ 当a≥0时，f′(x)＞0，函数f(x)在(0，＋∞)上单调递增．‎ 当a＜0时，令g(x)＝ax2＋(2a＋2)x＋a，‎ 由于Δ＝(2a＋2)2－4a2＝4(2a＋1)，‎ ‎①当a＝－时，Δ＝0，‎ f′(x)＝≤0，函数f(x)在(0，＋∞)上单调递减．‎ ‎②当a＜－时，Δ＜0，g(x)＜0，‎ f′(x)＜0，函数f(x)在(0，＋∞)上单调递减．‎ ‎③当－＜a＜0时，Δ＞0.‎ 设x1，x2(x1＜x2)是函数g(x)的两个零点，‎ 则x1＝，‎ x2＝.‎ 因为x1＝ ‎＝＞0，‎ 所以，x∈(0，x1)时，g(x)＜0，f′(x)＜0，函数f(x)单调递减，‎ x∈(x1，x2)时，g(x)＞0，f′(x)＞0，函数f(x)单调递增，‎ x∈(x2，＋∞)时，g(x)＜0，f′(x)＜0，函数f(x)单调递减．‎ 综上可得，当a≥0时，函数f(x)在(0，＋∞)上单调递增；当a≤－时，函数f(x)在(0，＋∞)上单调递减；当－＜a<0时，f(x)在，上单调递减，‎ 在上单调递增．‎ ‎21．，，[2014·山东卷] 在平面直角坐标系xOy中，椭圆C：＋＝1(a>b>0)的离心率为，直线y＝x被椭圆C截得的线段长为.‎ ‎(1)求椭圆C的方程．‎ ‎(2)过原点的直线与椭圆C交于A，B两点(A，B不是椭圆C的顶点)．点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M，N两点．‎ ‎　(i)设直线BD，AM的斜率分别为k1，k2，证明存在常数λ使得k1＝λk2，并求出λ的值；‎ ‎　(ii)求△OMN面积的最大值．‎ ‎21．解：(1)由题意知，＝，可得a2＝4b2.‎ 椭圆C的方程可简化为x2＋4y2＝a2.‎ 将y＝x代入可得x＝±.‎ 因此×＝，即a＝2，所以b＝1，‎ 所以椭圆C的方程为＋y2＝1.‎ ‎(2)(i)设A(x1，y1)(x1y1≠0)，D(x2，y2)，则B(－x1，－y1)．‎ 因为直线AB的斜率kAB＝，且AB⊥AD，‎ 所以直线AD的斜率k＝－.‎ 设直线AD的方程为y＝kx＋m，‎ 由题意知k≠0，m≠0.‎ 由消去y，得(1＋4k2)x2＋8mkx＋4m2－4＝0，‎ 所以x1＋x2＝－，‎ 因此y1＋y2＝k(x1＋x2)＋2m＝.‎ 由题意知x1≠－x2，‎ 所以k1＝＝－＝.‎ 所以直线BD的方程为y＋y1＝(x＋x1)．‎ 令y＝0，得x＝3x1，即M(3x1，0)．‎ 可得k2＝－.‎ 所以k1＝－k2，即λ＝－.‎ 因此，存在常数λ＝－使得结论成立．‎ ‎(ii)直线BD的方程y＋y1＝(x＋x1)，‎ 令x＝0，得y＝－y1，即N.‎ 由(i)知M(3x1，0)，‎ 所以△OMN的面积S＝×3|x1|×|y1|＝‎ |x1||y1|.‎ 因为|x1||y1|≤＋y＝1，当且仅当＝|y1|＝时，等号成立，‎ 此时S取得最大值，‎ 所以△OMN面积的最大值为.‎