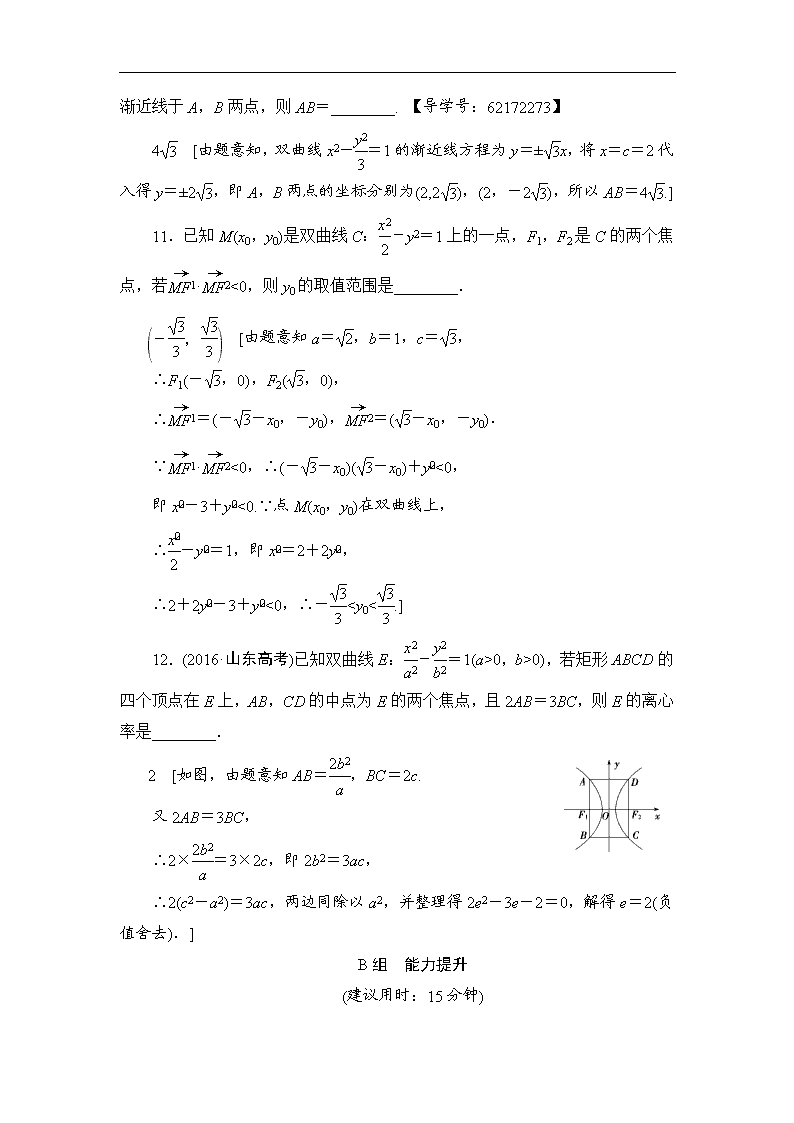高考数学 17-18版 第9章 第49课 课时分层训练49
课时分层训练(四十九)
A组 基础达标
(建议用时:30分钟)
1.双曲线x2-=1的两条渐近线方程为________.
y=±2x [由x2-=0得y=±2x,即双曲线的两条渐进线方程为y=±2x.]
2.已知双曲线-y2=1(a>0)的一条渐近线为x+y=0,则a=__________.
【导学号:62172271】
[双曲线-y2=1的渐近线为y=±,已知一条渐近线为x+y=0,即y=-x,因为a>0,所以=,所以a=.]
3.双曲线-=1的离心率为________.
[∵a2=4,b2=5,
∴c2=9,∴e==.]
4.若双曲线-=1的一条渐近线经过点(3,-4),则此双曲线的离心率为________. 【导学号:62172272】
[由双曲线的渐近线过点(3,-4)知=,∴=.
又b2=c2-a2,∴=,
即e2-1=,∴e2=,∴e=.]
5.已知点F1(-3,0)和F2(3,0),动点P到F1,F2的距离之差为4,则点P的轨迹方程为________.
-=1(x>0) [由题设知点P的轨迹方程是焦点在x
轴上的双曲线的右支,设其方程为-=1(x>0,a>0,b>0),由题设知c=3,a=2,b2=9-4=5.
所以点P的轨迹方程为-=1(x>0).]
6.已知F为双曲线C:x2-my2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为________.
[由双曲线方程知a2=3m,b2=3,
∴c==.
不妨设点F为右焦点,则F(,0).
又双曲线的一条渐近线为x-y=0,
∴d==.]
7.(2016·全国卷Ⅰ改编)已知方程-=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是________.
(-1,3) [∵原方程表示双曲线,且两焦点间的距离为4.
∴则
因此-1
0,即-20,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2AB=3BC,则E的离心率是________.
2 [如图,由题意知AB=,BC=2c.
又2AB=3BC,
∴2×=3×2c,即2b2=3ac,
∴2(c2-a2)=3ac,两边同除以a2,并整理得2e2-3e-2=0,解得e=2(负值舍去).]
B组 能力提升
(建议用时:15分钟)
1.已知F为双曲线C:-=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为________.
44 [由双曲线C的方程,知a=3,b=4,c=5,
∴点A(5,0)是双曲线C的右焦点,
且PQ=QA+PA=4b=16,
由双曲线定义,得PF-PA=6,
QF-QA=6.
∴PF+QF=12+PA+QA=28,
因此△PQF的周长为PF+QF+PQ=28+16=44.]
2.已知点F是双曲线-=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
(1,2) [由题意易知点F的坐标为(-c,0),A,B,E(a,0),∵△ABE是锐角三角形,∴·>0,
即·=·>0,整理得3e2+2e>e4,
∴e(e3-3e-3+1)<0,
∴e(e+1)2(e-2)<0,
解得e∈(0,2),又e>1,∴e∈(1,2).]
3.(2016·北京高考)双曲线-=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=__________.
2 [双曲线-=1的渐近线方程为y=±x,易得两条渐近线方程互相垂直,由双曲线的对称性知=1.
又正方形OABC的边长为2,所以c=2,
所以a2+b2=c2=8,因此a=2.]
4.已知双曲线-=1(a>0,b>0)的一个焦点为F(2,0),且双曲线的渐近线与圆(x-2)2+y2=3相切,则双曲线的方程为__________.
x2-=1 [由双曲线的渐近线y=±x,即bx±ay=0与圆(x-2)2+y2=3相切,
∴=,则b2=3a2.①
又双曲线的一个焦点为F(2,0),
∴a2+b2=4,②
联立①②,解得a2=1,b2=3.
故所求双曲线的方程为x2-=1.]
5.(2017·南通三模)在平面直角坐标系xOy中,双曲线-y2=1与抛物线y2=-12x有相同的焦点,则双曲线的两条渐近线的方程为________.
y=±x [抛物线y2=-12x的焦点为(-3,0),∴a2+1=9,∴a=±2.
∴双曲线的两条渐近线方程为y=±=±x.]
6.(2016·天津高考改编)已知双曲线-=1(b>0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD的面积为2b,则双曲线的方程为________.
-=1 [由题意知双曲线的渐近线方程为y=±x,圆的方程为x2+y2=4,联立
解得或
即第一象限的交点为.
由双曲线和圆的对称性得四边形ABCD为矩形,其相邻两边长为,,故=2b,得b2=12.
故双曲线的方程为-=1.]