北京市密云县2019-2020学年高一下学期期末考试数学试题

北京市密云县2019-2020学年高一下学期期末考试数学试题

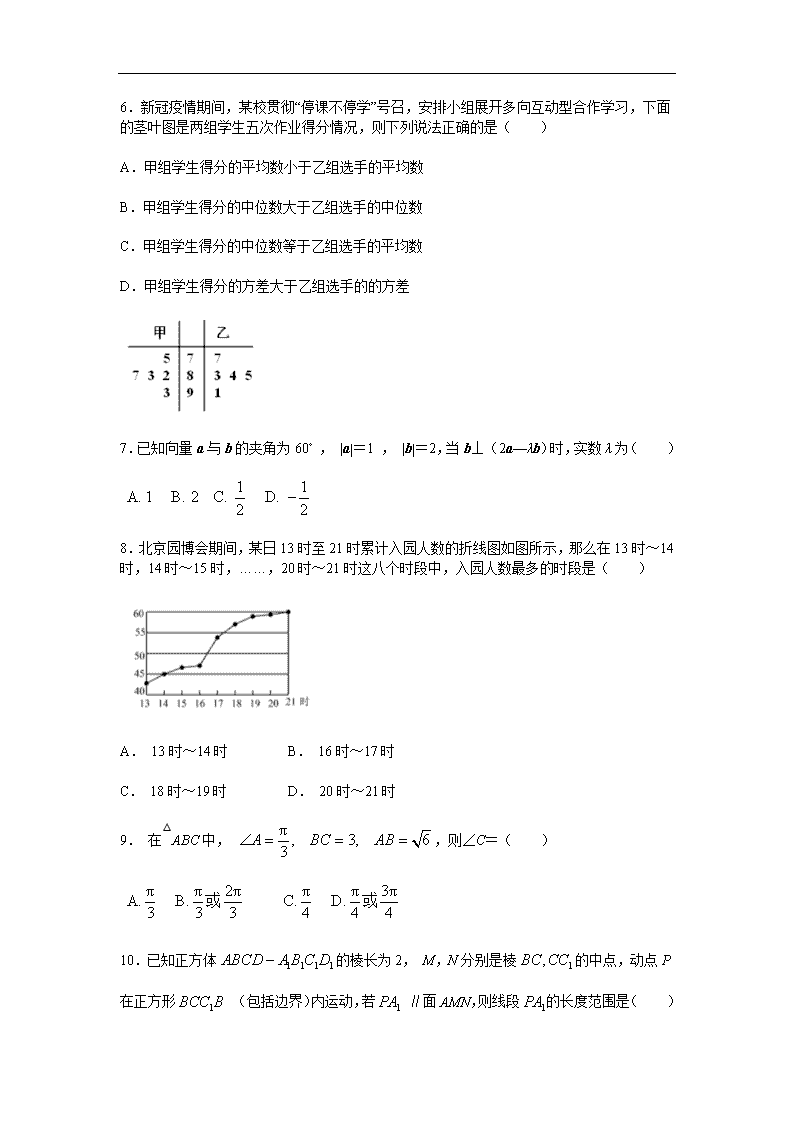
北京市密云县2019-2020学年高一下学期 期末考试试题 一、选择题：本大题共10小题，每小题4分，共40分，在每小题列出的四个选项中，选出符合题目要求的一项．‎ ‎1．已知点A(1，2)， B(－1，0)，则＝（ ）‎ А． （2，0） B． （2，2）‎ C． （－2，－2） D． （0，2）‎ ‎2．在复平面内，复数对应的点位于（ ）‎ A．第一象限 B．第二象限 C．第三象阳 D．第四象限 ‎3．某工厂有男员工56人，女员工42人，用分层抽样的方法，从全体员工中抽出一个容量为28的样本进行工作效率调查，其中男员工应抽的人数为（ ）‎ A． 16 B． 14‎ C． 28 D． 12‎ ‎4，在下列各组向量中，可以作为基底的是（ ）‎ ‎5．在空间中，下列结论正确的是（ ）‎ A．三角形确定一个平面 ‎ B．四边形确定一个平面 C．一个点和一条直线确定一个平面 ‎ D．两条直线确定一个平面 ‎ ‎ ‎6．新冠疫情期间，某校贯彻“停课不停学”号召，安排小组展开多向互动型合作学习，下面的茎叶图是两组学生五次作业得分情况，则下列说法正确的是（ ）‎ A．甲组学生得分的平均数小于乙组选手的平均数 B．甲组学生得分的中位数大于乙组选手的中位数 C．甲组学生得分的中位数等于乙组选手的平均数 D．甲组学生得分的方差大于乙组选手的的方差 ‎7．已知向量a与b的夹角为60° ， |a|＝1 ， |b|＝2，当b⊥（2a—λb）时，实数λ为（ ）‎ ‎8．北京园博会期间，某日13时至21时累计入园人数的折线图如图所示，那么在13时～14时，14时～15时，……，20时～21时这八个时段中，入园人数最多的时段是（ ）‎ ‎ ‎ A． 13时～14时 B． 16时～17时 C． 18时～19时 D． 20时～21时 ‎9． 在△ABC中， ，则∠C＝（ ）‎ ‎10．已知正方体的棱长为2， M，N分别是棱的中点，动点P在正方形 （包括边界）内运动，若 ∥面AMN，则线段的长度范围是（ ）‎ ‎ ‎ ‎ ‎ 二、填空题：本大共5小题，每小题5分，共25分．‎ ‎11．已知复数，则复数z＝________‎ ‎12．已知a ， b是平面α外的两条不同直线，给出下列三个论断：‎ ‎①a⊥bb； ②a⊥α； ③b∥α 以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：________.‎ ‎13．如图，在△ABC中， ．若，则λ的值为________，P是BN上的一点，若，则m的值为________.‎ ‎14．将底面直径为8，高为2的圆锥体石块打磨成一个圆柱，则该圆柱侧面积的最大值为________.‎ ‎15．下图是某地区2018年12个月的空气质量指数以及相比去年同期变化幅度的数据统计图表，根据图表，下面叙述正确的是________.‎ ‎ ‎ ‎①2月相比去年同期变化幅度最小，3月的空气质量指数最高；‎ ‎②第一季度的空气质量指数的平均值最大，第三季度的空气质量指数的平均值最小；‎ ‎③第三季度空气质量指数相比去年同期变化幅度的方差最小；‎ ‎④空气质量指数涨幅从高到低居于前三位的月份为6、8、4月．‎ 三、解答题：本大题共6小题，共85分，解答应写出文字说明，演算步骤或证明过程．‎ ‎16． （本小题满分14分）‎ 已知复数（i为虚数单位） ．‎ ‎（Ⅰ）求复数z的模|z|；‎ ‎（Ⅱ）求复数z的共轭复数；‎ ‎（Ⅲ）若z是关于x的方程一个虚根，求实数m的值．‎ ‎ ‎ ‎17． （本小题满分14分）‎ 已知向量a与b，a＝（1，0） ， b＝（－2，1）．‎ ‎（Ⅰ）求2a－b；‎ ‎（Ⅱ）设a， b的夹角为θ，求cosθ的值；‎ ‎（Ⅲ）若向量ka＋b与a＋kb互相平行，求k的值．‎ ‎18． （本小题满分14分）‎ 如图，在四棱锥P—ABCD中， PD⊥平面ABCD，底面ABCD为正方形， F为对角线AC与BD的交点， E为棱PD的中点．‎ ‎(I)证明： EF //平面PBC；‎ ‎(Ⅱ)证明： AC⊥PB．‎ ‎ ‎ ‎19． （本小题满分14分）‎ 在△ABC中，‎ ‎（Ⅰ）求∠A；‎ ‎（Ⅱ）求△ABC的面积．‎ ‎20． （本小题满分14分）‎ 某校为了解疫情期间学生线上学习效果，进行一次摸底考试，从中选取60名同学的成绩(百分制，均为正数)分成[40，50)，[50，60)，[60，70)， [70，80)， [80，90)，[90，100)六组后，得到部分频率分布直方图（如图），观察图形，回答下列问题：‎ ‎（I）求分数在[70，80）内的频率，并补全这个频率分布直方图；‎ ‎（Ⅱ）根据频率分布直方图，估计本次考试成绩的众数、均值；‎ ‎（Ⅲ）根据评奖规则，排名靠前10%的同学可以获奖，请你估计获奖的同学至少需要多少分？‎ ‎ ‎ ‎21． （本小题满分15分）‎ 如图1，在等腰梯形ABCD中， AB//CD， AB＝3， CD＝1， BC＝2， E、F分别为腰AD、 BC的中点．将四边形CDEF沿EF折起，使平面⊥平面ABFE，如图2， H，M别线段EF、AB的中点．‎ ‎（Ⅰ）求证： MHL平面；‎ ‎（Ⅱ）请在图2所给的点中找出两个点，使得这两点所在直线与平面垂直，并给出证明：‎ ‎（Ⅲ）若N为线段中点，在直线BF上是否存在点Q，使得NQ// 面 ？如果存在，求出线段NQ的长度，如果不存在，请说明理由．‎ ‎ ‎ ‎【参考答案】‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎