2019届二轮复习第4练 程序框图、合情推理与演绎推理学案(全国通用)
第4练 程序框图、合情推理与演绎推理
[明晰考情] 1.命题角度:程序框图的输出与填充是考查的重点;推理与证明在高考中少数年份考查,多以数表(阵)、图形、不等式等为背景考查合情推理.2.题目难度:中低档难度.
考点一 程序框图的输出
方法技巧 程序框图中循环结构是高考考查的重点,确定循环结构的输出结果要注意以下几点
(1)明确循环次数和循环条件,把握循环变量的变化情况.(2)模拟运行循环变量取初始值和最后几个值时输出结果的变化.
1.(2018·北京)执行如图所示的程序框图,输出的s值为( )
A. B. C. D.
答案 B
解析 第一步:s=1-=,k=2,k<3;第二步:s=+=,k=3,输出s.故选B.
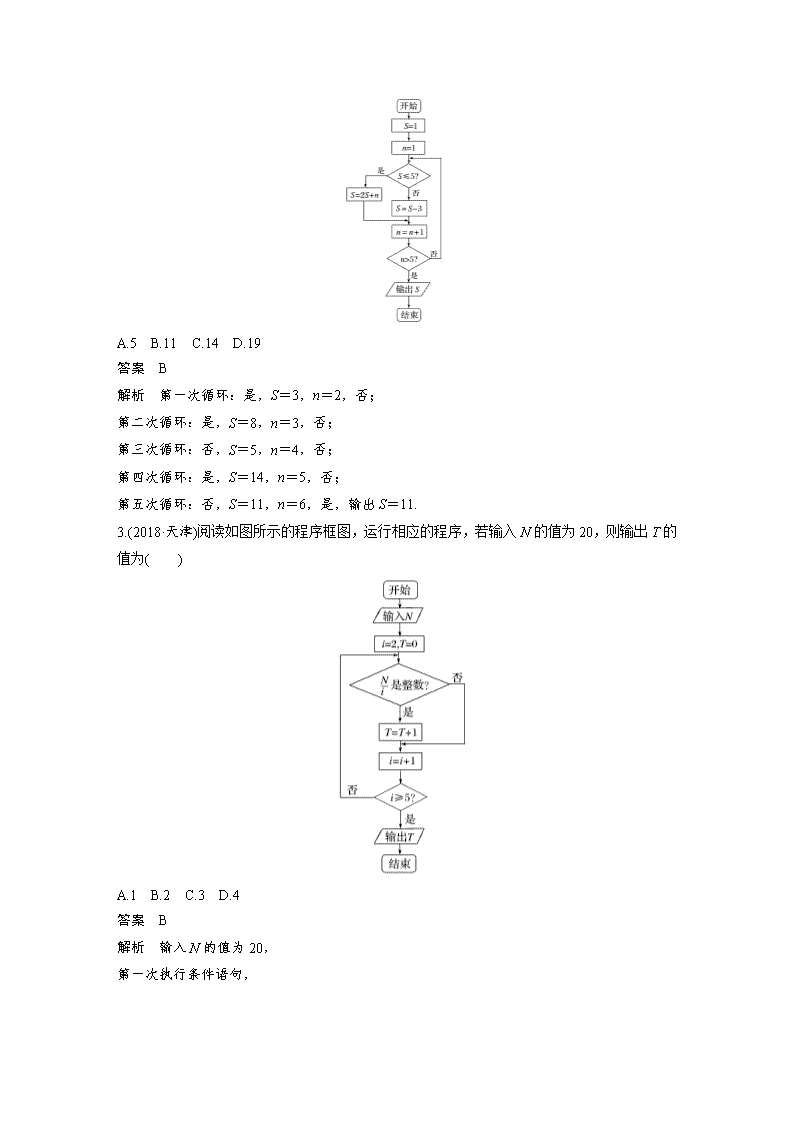
2.执行如图所示的程序框图,则输出S的值为( )
A.5 B.11 C.14 D.19
答案 B
解析 第一次循环:是,S=3,n=2,否;
第二次循环:是,S=8,n=3,否;
第三次循环:否,S=5,n=4,否;
第四次循环:是,S=14,n=5,否;
第五次循环:否,S=11,n=6,是,输出S=11.
3.(2018·天津)阅读如图所示的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为( )
A.1 B.2 C.3 D.4
答案 B
解析 输入N的值为20,
第一次执行条件语句,
N=20,i=2,=10是整数,
∴T=0+1=1,i=3<5;
第二次执行条件语句,
N=20,i=3,=不是整数,
∴i=4<5;
第三次执行条件语句,N=20,i=4,=5是整数,
∴T=1+1=2,i=5,此时i≥5成立,∴输出T=2.
故选B.
4.运行如图所示的程序框图,则输出的S的值为________.
答案
解析 S=0+=1-,i=2;S=1-+-=1-,i=3;S=1-,i=4;S=1-,i=5;…,
可知输出的S=1-=.
考点二 程序框图的填充
方法技巧 (1)条件结构的程序框图可结合分段函数的思想根据输出结果确定填充内容.
(2)循环结构的程序框图可先假设i>n或i
-2;
当n=99时,S=-lg 100=-2,跳出循环,
故①中应填n<99?.
考点三 合情推理
方法技巧 (1)归纳推理的思维步骤:发现共性,归纳猜想,结论验证.
(2)类比推理的思维步骤:观察比较,联想类推,猜测结论.
9.(2018·安庆模拟)对大于1的自然数的三次幂可以分解成几个奇数的和,比如23=3+5,33=7+9+11,43=13+15+17+19,…,以此规律,则453的分解和式中一定不含有( )
A.2 069 B.2 039 C.2 009 D.1 979
答案 D
解析 由规律得n3中有n项,而23,33,43中第一项分别为2×2-1,2×4-1=2×(2+2)-1,2×7-1=2×(2+2+3)-1,
所以453中第一项为2×(2+2+3+4+…+44)-1=1 981,
所以一定不含有1 979.
10.一个三角形可分为以内切圆半径为高,以原三角形三条边为底的三个三角形,类比此方法,若一个三棱锥的体积V=2,表面积S=3,则该三棱锥内切球的体积为( )
A.81π B.16π C. D.
答案 C
解析 由一个三角形可分为以内切圆半径为高,以原三角形三条边为底的三个三角形,可以类比一个三棱锥分为以内切球半径为高,以原三棱锥四个面为底面的四个三棱锥.
设三棱锥的四个面的表面积分别为S1,S2,S3,S4,由于内切球到各面的距离等于内切球的半径,
∴V=(S1×r+S2×r+S3×r+S4×r)=S×r,
∴内切球半径r===2,
∴该三棱锥内切球的体积为π·23=.
11.已知12=×1×2×3,12+22=×2×3×5,12+22+32=×3×4×7,12+22+32+42=×4×5×9,则12+22+…+n2=________.(其中n∈N*)
答案 n(n+1)(2n+1)
解析 根据题意可归纳出12+22+…+n2=n(n+1)·(2n+1),下面给出证明:(k+1)3-k3=3k2+3k+1,则23-13=3×12+3×1+1,33-23=3×22+3×2+1,…,(n+1)3-n3=3n2+3n+1,累加得(n+1)3-13=3(12+22+…+n2)+3(1+2+…+n)+n,整理得12+22+…+n2=n(n+1)(2n+1).
12.给出下面四个类比结论:
①实数a,b,若ab=0,则a=0或b=0;类比复数z1,z2,若z1·z2=0,则z1=0或z2=0;
②实数a,b,若ab=0,则a=0或b=0;类比向量a,b,若a·b=0,则a=0或b=0;
③实数a,b,若a2+b2=0,则a=b=0;类比复数z1,z2,有z+z=0,则z1=z2=0;
④实数a,b,若a2+b2=0,则a=b=0;类比向量a,b,若a2+b2=0,则a=b=0.
其中类比结论正确的个数是________.
答案 2
解析 ①显然正确;②中若a⊥b,则a·b=0,∴②错误;
③中取z1=1,z2=i,则z+z=0,∴③错误;
④中a2=|a|2,b2=|b|2,若a2+b2=0,则|a|=|b|=0,
∴a=b=0,∴④正确.综上,正确结论的个数是2.
考点四 演绎推理
方法技巧 新定义问题是演绎推理问题的重要形式,这类题目的解题思路:读懂新定义的含义,在领会新定义实质的基础上,将其应用在具体情境中进行演绎推理,得到新的结论.
13.下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180°
B.由平面三角形的性质,推测空间四面体的性质
C.某校高三共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人
D.在数列{an}中,a1=1,an=(n≥2),计算a2,a3,a4,由此推测通项an
答案 A
解析 演绎推理是由一般到特殊的推理,显然选项A符合;选项B属于类比推理;选项C,D是归纳推理.
14.1748年,瑞士著名数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式eix=cos x+isin x,这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”,根据此公式可知,e2i表示的复数所对应的点在复平面中位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案 B
解析 由已知得e2i=cos 2+isin 2,它表示的复数在复平面中对应的点为(cos 2,sin 2).由于<2<π,故cos 2<0,sin 2>0,所以e2i表示的复数所对应的点在复平面中位于第二象限.故选B.
15.“斐波那契”数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常被人们称之为神奇数.具体数列为:1,1,2,3,5,8,…,即从该数列的第三项数字开始,每个数字等于前两个相邻数字之和.已知数列{an}为“斐波那契”数列,Sn为数列{an}的前n项和,则
(1)S7=________;
(2)若a2 017=m,则S2 015=________.(用m表示)
答案 (1)33 (2)m-1
解析 (1)S7=1+1+2+3+5+8+13=33.
(2)∵an+2=an+an+1=an+an-1+an
=an+an-1+an-2+an-1
=an+an-1+an-2+an-3+an-2
=…
=an+an-1+an-2+an-3+…+a2+a1+1,
∴S2 015=a2 017-1=m-1.
16.对于任意的两个实数对(x1,y1)和(x2,y2),规定:(x1,y1)=(x2,y2),当且仅当运算“⊗”为(x1,y1)⊗(x2,y2)=(x1x2-y1y2,y1x2+x1y2);运算“⊕”为(x1,y1)⊕(x2,y2)=(x1+x2,y1+y2).设k,n∈R,若(1,2)⊗(k,n)=(3,1),则(1,2)⊕(k,n)=________.
答案 (2,1)
解析 由(1,2)⊗(k,n)=(k-2n,2k+n)=(3,1),
所以 解得
所以(1,2)⊕(k,n)=(1,2)⊕(1,-1)=(2,1).
1.运行如图所示的程序框图,若输出的结果为,则判断框内可以填( )
A.k>2 020? B.k≥2 020?
C.k≥2 019? D.k>2 019?
答案 C
解析 执行程序框图可知,该程序是计算=各项的和,
即s==,当k=2 017时,s=,则判断框内可以填k≥2 019?故选C.
2.(2017·全国Ⅱ)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
A.乙可以知道四人的成绩
B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩
答案 D
解析 由甲说:“我还是不知道我的成绩”可推知甲看到乙、丙的成绩为“1个优秀,1个良好”.乙看丙的成绩,结合甲的说法,丙为“优秀”时,乙为“良好”;丙为“良好”时,乙为“优秀”,可得乙可以知道自己的成绩.丁看甲的成绩,结合甲的说法,甲为“优秀”时,丁为“良好”;甲为“良好”时,丁为“优秀”,可得丁可以知道自己的成绩.
解题秘籍 (1)程序运行的输出结果可以模拟运行的过程,列出了每一步运行后变量的取值.
(2)循环结构要把握循环中止的条件,注意赋值的先后顺序不同对变量取值的影响.
(3)实际问题和推理相结合,要按照可能发生的情况全面论证,去伪存真,找到问题的答案.
1.某市乘坐出租车的收费办法如下:不超过4千米的里程收费12元;超过4千米的里程按每千米2元收费(对于其中不足1千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);当里程超过4千米时,另收燃油附加费1元.相应系统收费的程序框图如图所示,其中x(单位:千米)为行驶里程,y(单位:元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
A.y=2+4 B.y=2+5
C.y=2+4 D.y=2+5
答案 D
解析 由题意,得当x>4时,所收费用y=12+×2+1=2+5,故选D.
2.执行如图所示的程序框图,若要使输入的x值与输出的y值相等,则这样的x值的个数是( )
A.1 B.2 C.3 D.4
答案 D
解析 该程序的功能是计算并输出分段函数y=的函数值.当x≤1时,由x3=x,解得x=-1或x=0或x=1,这三个x值均满足条件;
当1<x≤3时,由3x-3=x,解得x=,满足条件;
当x>3时,由=x,解得x=-1或x=1,这两个x值均不满足条件.
综上所述,满足条件的x值的个数是4,故选D.
3.(2016·全国Ⅰ)执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x C.y=4x D.y=5x
答案 C
解析 执行题中的程序框图知,
第一次进入循环体:x=0+=0,y=1×1=1,x2+y2<36;
第二次执行循环体:n=1+1=2,x=0+=,y=2×1=2,x2+y2<36;
第三次执行循环体:n=2+1=3,x=+=,y=3×2=6,x2+y2>36,满足x2+y2≥
36,故退出循环,输出x=,y=6,满足y=4x,故选C.
4.(2018·衡水金卷模拟)执行如图所示的程序框图,若输入的t=0.05,则输出的n为( )
A.3 B.4 C.5 D.6
答案 C
解析 根据给定的程序可知,第一次循环S=,m=,n=1,成立;第二次循环S=,m=,n=2,成立;第三次循环S=,m=,n=3,成立;第四次循环S=,m=,n=4,成立;第五次循环S=,m=,n=5,不成立.此时结束循环,所以输出的n为5,故选C.
5.某程序框图如图所示,若输出的S=26,则判断框内应填( )
A.k>3? B.k>4? C.k>5? D.k>6?
答案 A
解析 第一次循环:k=2,S=4;
第二次循环:k=3,S=11;
第三次循环:k=4,S=26;
若输出S=26,则应该退出循环,故判断框内可填k>3?.
6.已知f1(x)=sin x+cos x,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2 019(x)等于( )
A.sin x+cos x B.-sin x-cos x C.sin x-cos x D.-sin x+cos x
答案 B
解析 f2(x)=f1′(x)=cos x-sin x,f3(x)=f2′(x)=-sin x-cos x,f4(x)=f3′(x)=-cos x+sin x,f5(x)=f4′(x)=sin x+cos x,f6(x)=f5′(x)=cos x-sin x,…,
∴fn(x)=fn+4(x),
∵2 019=504×4+3,
∴f2 019(x)=f3(x)=-sin x-cos x,故选B.
7.(2018·重庆调研)为培养学生分组合作能力,现将某班分成A,B,C三个小组,甲、乙、丙三人分到不同组.某次数学建模考试中三人成绩情况如下:在B组中的那位的成绩与甲不一样,在A组中的那位的成绩比丙低,在B组中的那位的成绩比乙低.若甲、乙、丙三人按数学建模考试成绩由高到低排序,则排序正确的是( )
A.甲、丙、乙 B.乙、甲、丙 C.乙、丙、甲 D.丙、乙、甲
答案 C
解析 因为在B组中的那位的成绩与甲不一样,在B组中的那位的成绩比乙低.所以甲、乙都不在B组,所以丙在B组. 假设甲在A组,乙在C组,由题意得甲、乙、丙三人按数学建模考试成绩由高到低排序是乙、丙、甲.假设甲在C组,乙在A组,由题意,得矛盾.所以排序正确的是乙、丙、甲.故选C.
8.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
A.9 B.18 C.20 D.35
答案 B
解析 初始值n=3,x=2,程序运行过程如下:
v=1,
i=2→v=1×2+2=4,
i=1→v=4×2+1=9,
i=0→v=9×2+0=18,
i=-1,跳出循环,输出v=18,故选B.
9.如图所示的一个算法的程序框图,则输出d的最大值为________.
答案 1+
解析 由程序框图得,d表示的就是上半圆x2+y2=1(y≥0)上的点到直线x-y-2=0的距离,由数形结合可以得到dmax=+1=1+.
10.在侦破某一起案件时,警方要从甲、乙、丙、丁四名可疑人员中查出真正的嫌疑人,现有四条明确信息:(1)此案是两人共同作案;(2)若甲参与此案,则丙一定没参与;(3)若乙参与此案,则丁一定参与;(4)若丙没参与此案,则丁也一定没参与.据此可以判断参与此案的两名嫌疑人是________.
答案 丙、丁
解析 由(1)(3)(4)可知,乙没参与此案;若甲参与此案,则丙、丁没参与此案,不符合(1),故丙、丁参与此案,全部符合.
11.如图是一个程序框图,则输出的S的值为________.
答案 125
解析 S=1,i=1<4,
S=1×5=5,i=1+1=2<4,
S=5×5=25,i=2+1=3<4,
S=25×5=125,i=3+1=4,结束循环,
则输出的S=125.
12.(2018·长春模拟)在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学考了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是________.
答案 甲
解析 如果甲说的是真话,则乙、丙、丁都是假话,此时丙与丁是矛盾的,所以不成立;
如果乙说的是真话,则甲、丙、丁都是假话,此时丙与丁是矛盾的,所以不成立;
如果丙说的是真话,则甲、乙、丁都是假话,此时甲与丙是矛盾的,所以不成立;
所以只有丁说的是真话,此时甲、乙、丙都是假话,可推得甲得了满分,
故考满分的同学是甲.