2021届课标版高考文科数学大一轮复习课件：§8-4 直线、平面垂直的判定与性质（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§8-4 直线、平面垂直的判定与性质（讲解部分）

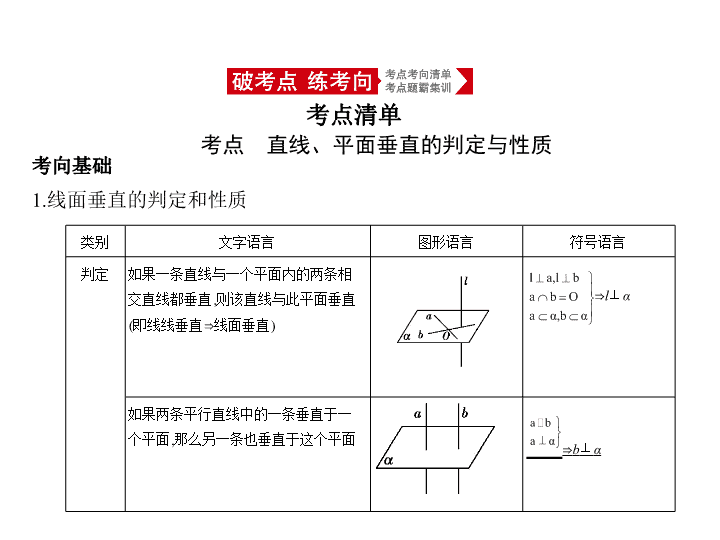
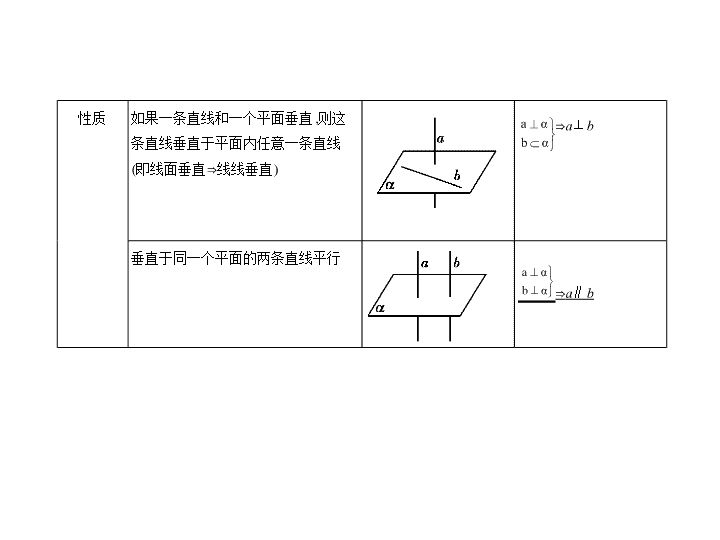
专题八　立体几何 §8.4 　直线、平面垂直的判定与性质 高考文数 考点　直线、平面垂直的判定与性质 考点清单 考向基础 1.线面垂直的判定和性质 类别 文字语言 图形语言 符号语言 判定 如果一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直(即线线垂直 ⇒ 线面垂直)     ⇒ l ⊥ α 如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面     ⇒ b ⊥ α 性质 如果一条直线和一个平面垂直,则这条直线垂直于平面内任意一条直线 (即线面垂直 ⇒ 线线垂直)     ⇒ a ⊥ b 垂直于同一个平面的两条直线平行     ⇒ a ∥ b 类别 文字语言 图形语言 符号语言 判定 两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直   ∠ AOB 是二面角 α - l - β 的 平面角,且∠ AOB =90 ° , 则 α ⊥ β 如果一个平面过另一个平面的垂线,则这两个平面互相垂直(即线面垂直 ⇒ 面面垂直)     ⇒ α ⊥ β 2.面面垂直的判定和性质 性质 如果两个平面垂直,则其中一个平面内垂直于交线的直线垂直于另一个平面     ⇒ l ⊥ α 如果两个相交平面同时垂直于第三个平面,那么它们的交线垂直于第三个平面     ⇒ l ⊥ γ 3.直线与平面所成的角 (1)斜线与平面所成的角的定义:平面的一条斜线和它在这个平面内的射影 所成的 锐角 ,叫做这条直线和这个平面所成的角. (2)当一条直线垂直于平面时,规定它们所成的角是直角;当一条直线和平 面平行或在平面内时,规定它们所成的角大小为0 ° . (3)直线 l 与平面 α 所成角 θ 的取值范围 4.二面角 (1)二面角的定义:由两个半平面和一条公共交线所组成的空间图形叫做二 面角.公共交线叫做该二面角的棱.两个半平面叫做二面角的面. 直线 l 和平面 α 的位置关系 l ⊂ α 或 l ∥ α l ⊥ α l 和 α 斜交 θ 的取值范围 θ =0 ° θ =90 ° 0 ° < θ <90 ° (2)二面角的平面角 以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条 射线,这两条射线所组成的角叫做二面角的平面角.若记此角为 θ ,当 θ =90 ° 时,二面角叫做直二面角. 例1　如图,正方形 SG 1 G 2 G 3 中, E , F 分别是 G 1 G 2 , G 2 G 3 的中点,现沿 SE , SF , EF 把 这个正方形折成一个四面体,使 G 1 , G 2 , G 3 三点重合,重合后的点记为 G .给出 下列关系: ① SG ⊥平面 EFG ;② SE ⊥平面 EFG ;③ GF ⊥ SE ;④ EF ⊥平面 SEG .其中成立 的有   (　　)   A.①与②　    B.①与③ C.②与③　    D.③与④ 考向一　线面垂直的判定与性质 考向突破 解析　由 SG ⊥ GE , SG ⊥ GF , GE ∩ GF = G ,得 SG ⊥平面 EFG ,故①正确;若 SE ⊥平面 EFG ,则 SG ∥ SE ,这与 SG ∩ SE = S 矛盾,故②错误;易知 GF ⊥ SG , GF ⊥ EG ,且 SG ∩ EG = G ,所以 GF ⊥平面 SEG ,又 SE ⊂ 平面 SEG ,所以 GF ⊥ SE ,故③ 正确;若 EF ⊥平面 SEG ,则 EF ∥ GF ,这与 EF ∩ GF = F 矛盾,故④错误.故正确 的为①与③,故选B. 答案    B 例2    如图所示,在四边形 ABCD 中, AD ∥ BC , AD = AB ,∠ BCD =45 ° ,∠ BAD = 90 ° ,将△ ABD 沿 BD 折起,使得平面 ABD ⊥平面 BCD ,构成四面体 ABCD ,则在 四面体中,下列说法正确的是(　　)   A.平面 ABD ⊥平面 ABC 　    B.平面 ACD ⊥平面 BCD C.平面 ABC ⊥平面 BCD 　    D.平面 ACD ⊥平面 ABC 考向二　面面垂直的判定与性质 解析　∵在四边形 ABCD 中, AD ∥ BC ,∠ BCD =45 ° , ∴∠ ADC =135 ° , ∵ AD = AB ,∠ BAD =90 ° ,∴∠ ADB =45 ° , ∴∠ BDC =90 ° ,∴ BD ⊥ CD . 又在四面体 ABCD 中,平面 ABD ⊥平面 BCD ,且平面 ABD ∩ 平面 BCD = BD , ∴ CD ⊥平面 ABD ,∴ CD ⊥ AB , 又 AD ⊥ AB , AD ∩ CD = D ,∴ AB ⊥平面 ACD , 又 AB ⊂ 平面 ABC ,∴平面 ABC ⊥平面 ADC .故选D. 答案    D 方法1 　证明线线垂直的方法 1.线线垂直的定义(计算两直线所成的角大小为90 ° ). 2.利用平面几何中证明线线垂直的方法:①特殊图形中的垂直关系;② 等腰 三角形底边中线的性质 ;③ 勾股定理的逆定理; ④圆周角定理的推论等. 3.线面垂直的性质(详见考点清单). 4.三垂线定理及其逆定理. 方法技巧 例1　如图,已知矩形 ABCD ,过 A 作 SA ⊥平面 ABCD ,再过 A 作 AE ⊥ SB 交 SB 于 点 E ,过 E 作 EF ⊥ SC 交 SC 于点 F . (1)求证: AF ⊥ SC ; (2)若平面 AEF 交 SD 于点 G ,求证: AG ⊥ SD .   证明　(1)因为 SA ⊥平面 ABCD , BC ⊂ 平面 ABCD , 所以 SA ⊥ BC . 因为四边形 ABCD 为矩形,所以 AB ⊥ BC , 又因为 SA ∩ AB = A , 所以 BC ⊥平面 SAB ,所以 BC ⊥ AE . 又 SB ⊥ AE , SB ∩ BC = B ,所以 AE ⊥平面 SBC ,所以 AE ⊥ SC . 又 EF ⊥ SC , EF ∩ AE = E ,所以 SC ⊥平面 AEF ,所以 AF ⊥ SC . (2)因为 SA ⊥平面 ABCD ,所以 SA ⊥ DC . 又 AD ⊥ DC , AD ∩ SA = A ,所以 DC ⊥平面 SAD ,所以 DC ⊥ AG . 由(1)知 SC ⊥平面 AEF ,又 AG ⊂ 平面 AEF , 所以 SC ⊥ AG ,所以 AG ⊥平面 SDC ,所以 AG ⊥ SD . 方法2 　证明线面垂直的方法 1.线面垂直的定义(一般不好验证任意性). 2.线面垂直的判定定理: a ⊥ b , a ⊥ c , b ∩ c = M , b ⊂ α , c ⊂ α ⇒ a ⊥ α . 3.平行线垂直平面的传递性: a ∥ b , a ⊥ α ⇒ b ⊥ α . 4.面面垂直的性质定理: α ⊥ β , α ∩ β = l , a ⊥ l , a ⊂ β ⇒ a ⊥ α . 5.面面平行的性质: α ∥ β , a ⊥ β ⇒ a ⊥ α . 例2    (2020届江西南昌第一次摸底考试,18)如图,已知在直三棱柱 ABC - A 1 B 1 C 1 中, AB ⊥ AC , AB = AC = AA 1 =2, E 是 BC 的中点, F 是 A 1 E 上一点,且 A 1 F =2 FE . (1)证明: AF ⊥平面 A 1 BC ; (2)求三棱锥 C 1 - A 1 FC 的体积.   解析　(1)证明:连接 AE ,依题意得△ ABC 为等腰直角三角形,所以 AE ⊥ BC , 由面积相等得   AB · AC =   BC · AE ,故 AE =   .   因为三棱柱 ABC - A 1 B 1 C 1 是直三棱柱, 所以 AA 1 ⊥平面 ABC , 所以 AA 1 ⊥ AE , AA 1 ⊥ BC . 在Rt△ A 1 AE 中,又因为 AA 1 =2, AE =   , 所以 A 1 E =   ,又因为 A 1 F =2 FE ,所以 EF =   A 1 F =   . 又因为   =   =   ,∠ AEA 1 =∠ AEA 1 , 所以△ AEF ∽△ A 1 EA ,故∠ AFE 为直角,即 AF ⊥ A 1 E .   (3分) 由 AE ⊥ BC , AA 1 ⊥ BC , AA 1 ∩ AE = A , 得 BC ⊥平面 A 1 AE ,所以 BC ⊥ AF . 由 AF ⊥ A 1 E , AF ⊥ BC , BC ∩ A 1 E = E ,得 AF ⊥平面 A 1 BC .   (6分) (2)过 E 作 ED ⊥ AC ,连接 A 1 D ,过 F 作 FG ∥ ED ,交 A 1 D 于点 G . 因为 AA 1 ⊥平面 ABC , ED ⊂ 平面 ABC ,所以 AA 1 ⊥ ED . 又因为 ED ⊥ AC , AC ∩ AA 1 = A , 故 ED ⊥平面 AA 1 C ,又 FG ∥ ED ,所以 FG ⊥平面 AA 1 C .   (9分) 则 FG =   ED =   ×   AB =   ,   =   × 2 × 2=2, 所以   =   =     · FG =   × 2 ×   =   .   (12分) 方法3 　证明面面垂直的方法 1.面面垂直的定义(作出两平面构成的二面角的平面角,计算其平面角大小 为90 ° ). 2.面面垂直的判定定理: a ⊥ β , a ⊂ α ⇒ α ⊥ β . 例3    (2018江苏,15,14分)在平行六面体 ABCD - A 1 B 1 C 1 D 1 中, AA 1 = AB , AB 1 ⊥ B 1 C 1 . 求证:(1) AB ∥平面 A 1 B 1 C ; (2)平面 ABB 1 A 1 ⊥平面 A 1 BC .     证明　(1)在平行六面体 ABCD - A 1 B 1 C 1 D 1 中, AB ∥ A 1 B 1 . 因为 AB ⊄ 平面 A 1 B 1 C , A 1 B 1 ⊂ 平面 A 1 B 1 C , 所以 AB ∥平面 A 1 B 1 C . (2)在平行六面体 ABCD - A 1 B 1 C 1 D 1 中,四边形 ABB 1 A 1 为平行四边形. 又因为 AA 1 = AB ,所以四边形 ABB 1 A 1 为菱形, 所以 AB 1 ⊥ A 1 B . 因为 AB 1 ⊥ B 1 C 1 , BC ∥ B 1 C 1 ,所以 AB 1 ⊥ BC . 又因为 A 1 B ∩ BC = B , A 1 B ⊂ 平面 A 1 BC , BC ⊂ 平面 A 1 BC , 所以 AB 1 ⊥平面 A 1 BC , 又因为 AB 1 ⊂ 平面 ABB 1 A 1 ,所以平面 ABB 1 A 1 ⊥平面 A 1 BC . 方法4 　翻折问题的处理方法 解决平面图形翻折为空间图形问题的关键是 看翻折前后线线位置关系的 变化 ,根据翻折的过程找到翻折前后线线位置关系中没有变化的量和发生 变化的量,这些不变的量和变化的量反映了翻折后的空间图形的结构特征. 例4    (2019全国统一诊断卷A,18)在五边形 ABCDF 中, E 是边 DF 上的点, AF ∥ BE ∥ CD , BC ∥ DF , BC ⊥ CD , AB = BC =   , AF = EF =1, BE = CD =2,如图1.将四 边形 AFEB 沿 BE 折起,使平面 AFEB ⊥平面 BCDE ,将△ BCD 沿 BD 折起,使点 C 与点 A 重合,重合的点记为 M ,如图2. (1)连接 EM ,证明:平面 BDM ⊥平面 DEM ; (2)求点 E 到平面 BDM 的距离.   解析　(1)证明:因为 EM =   =   , MB =   , BE =2, 所以 EM 2 + MB 2 = BE 2 ,所以 MB ⊥ EM . 又因为 BC ⊥ CD ,即 MB ⊥ MD , EM ∩ MD = M , EM ⊂ 平面 DEM , MD ⊂ 平面 DEM ,所以 MB ⊥平面 DEM .   (4分) 因为 MB ⊂ 平面 BDM ,所以平面 BDM ⊥平面 DEM .   (5分) (2)易知∠ BED =90 ° ,所以 S △ BED =   BE · ED =   . 又 MF ∥ BE , BE ⊂ 平面 BED , MF ⊄ 平面 BED , 所以 MF ∥平面 BED . 因为平面 BEFM ⊥平面 BED ,平面 BEFM ∩ 平面 BED = BE , EF ⊥ BE ,所以 EF ⊥ 平面 BED ,所以 EF 是三棱锥 M - BED 的高,   (7分) 所以 V M - BED =   S △ BED · EF =   .   (8分) 又知△ BMD 是直角三角形,所以 S △ BMD =   BM · MD =   . 设点 E 到平面 BDM 的距离为 h , 则 V E - BDM =   ×   h ,   (10分) 因为 V M - BED = V E - BDM ,所以   =   ×   h ,得 h =1, 即点 E 到平面 BDM 的距离为1.   (12分)