2018-2019学年福建省泉州市泉港区第一中学高二上学期期末考试 数学（文） word版

2018-2019学年福建省泉州市泉港区第一中学高二上学期期末考试 数学（文） word版

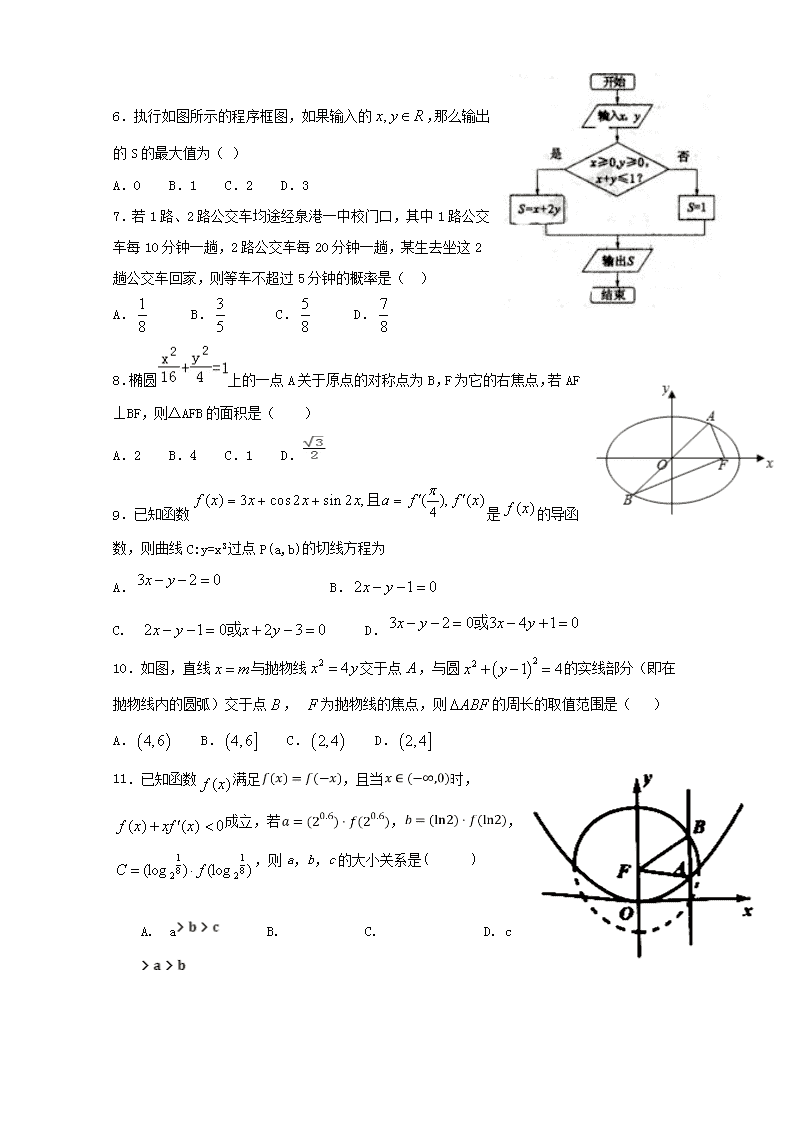
泉港一中2018-2019学年度高二（上）文科数学试卷 考试时间：120分钟；‎ 第I卷（选择题)‎ 一、单选题(每题5分，共60分)‎ ‎1．下面属于相关关系的是(　　)‎ A．圆的周长和它的半径之间的关系 B．价格不变的条件下，商品销售额与销售量之间的关系 C．家庭收入愈多，其消费支出也有增长的趋势 D．正方形的面积和它的边长之间的关系 ‎2．某单位青年、中年、老年职员的人数之比为10∶8∶7，从中抽取200名职员作为样本，若每人被抽取的概率是0.2，则该单位青年职员的人数为(　　)‎ A．280 B．320 C．400 D．1000‎ ‎3．0＜x＜2是不等式|x＋1|＜3成立的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．如果椭圆的弦被点（1，1）平分，则这条弦所在的直线方程是（　　）‎ A．x+2y﹣3=0 B．2x﹣y﹣3=0 C．2x+y﹣3=0 D．x+2y+3=0‎ ‎5．下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据：‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.5‎ t ‎4‎ ‎4.5‎ 根据上表提供的数据，求出y关于x的线性回归方程为，那么表中t的值为(　　)‎ A．4.5 B．3.15 C．3.5 D．3‎ ‎6．执行如图所示的程序框图，如果输入的，那么输出的S的最大值为（ ）‎ A．0 B．1 C．2 D．3‎ 7． 若1路、2路公交车均途经泉港一中校门口，其中1路公交车每10分钟一趟，2路公交车每20分钟一趟，某生去坐这2趟公交车回家，则等车不超过5分钟的概率是（ ）‎ A． B． C． D．‎ ‎8．椭圆上的一点A关于原点的对称点为B，F为它的右焦点，若AF⊥BF，则△AFB的面积是（　　）‎ A．2 B．4 C．1 D．‎ ‎9．已知函数是的导函数，则曲线C:y=x3过点P(a,b)的切线方程为 A． B．‎ C. D．‎ ‎10．如图，直线与抛物线交于点，与圆的实线部分（即在抛物线内的圆弧）交于点， 为抛物线的焦点，则的周长的取值范围是（ ）‎ A． B． C． D．‎ ‎11．已知函数满足，且当时，成立，若，，，则a，b，c的大小关系是(   )‎ A. a B. C. D. c ‎12.已知点P在曲线y=上,α为曲线在点P处的切线的倾斜角,则α的取值范围是(　　)‎ ‎(A) (B) (C) (D) ‎ 第II卷（非选择题)‎ 二、填空题（每题5分，共20分）‎ ‎13．命题“∀x∈R，|x|+x2>0”的否定是 ‎ ‎14．将八进制数123(8)转化为二进制数是 ‎ ‎15．为参加CCTV举办的中国汉字听写大赛，某中学举行了一次大型选拔活动，随机统计了甲、乙两班各6名学生的汉字听写的成绩如图所示，设甲的众数为x, 乙的中位数为y,则x-y= ‎ ‎16．已知函数，给出下列结论：‎ ‎①的单调递减区间；‎ ‎②当时，直线y=k与y=f （x）的图象有两个不同交点；‎ ‎③函数y=f（x）的图象与的图象没有公共点；‎ ④当时，函数的最小值为2．‎ 其中正确结论的序号是 ‎ 三、解答题:(共6题，70分)‎ ‎17.（本题10分 ）已知命题P：方程：表示焦点在y轴上的椭圆，命题q：双曲线的离心率，若“p∧q”为假命题，“p∨q”为真命题，求m的取值范围．‎ ‎18．（本题12分 ）已知抛物线C：y2=2px（p＞0）的焦点为F（1，0），抛物线E：x2=2py的焦点为M．（1）若过点M的直线l与抛物线C有且只有一个交点，求直线l的方程；‎ ‎（2）若直线MF与抛物线C交于A、B两点，求△OAB的面积．‎ ‎19．（本题12分 ）“砥砺奋进的五年”，泉州市经济社会发展取得新成就.自2012年以来，泉州市城乡居民收入稳步增长.随着扩大内需，促进消费等政策的出台，居民消费支出全面增长，消费结构持续优化升级，城乡居民人均可支配收入快速增长，人民生活品质不断提升.下图是泉州市2012-2016年城乡居民人均可支配收入实际增速趋势图（例如2012年，泉州城镇居民收入实际增速为7.3%，农村居民收入实际增速为8.2%）.‎ ‎ ‎ ‎（Ⅰ）从2012-2016五年中任选一年，求城镇居民收入实际增速大于7%的概率；‎ ‎（Ⅱ）从2012-2016五年中任选二年，求至少有一年农村和城镇居民收入实际增速均超过7%的概率；‎ ‎20．（本题12分 ）已知函数 ‎（1当a=2,b=1时，若方程=m的有2个实根，求m的值；‎ ‎（2）当时，若f(x)在(0，＋∞)上为增函数，求实数a的取值范围．‎ ‎21．（本题12分 ）椭圆： 的离心率为，过其右焦点与长轴垂直的直线与椭圆在第一象限相交于点， .（1）求椭圆的标准方程；‎ ‎（2）设椭圆的左顶点为，右顶点为，点是椭圆上的动点，且点与点， 不重合，直线与直线相交于点，直线与直线相交于点，求证：以线段为直径的圆恒过定点.‎ ‎22．已知函数 ．‎ ‎（1）求函数 的单调区间和极值；‎ ‎（2）如果，证明 ．‎ 泉港一中2018-2019学年度高二（上）文科试题参考答案 ‎1C 2．C 3．A 4.A 5．D 6．C 7．C 8．B 9．D ‎10．A 11．C 12.D 二、填空题（每题5分，共4题）‎ ‎13．命题“∀x∈R，|x|+x2>0”的否定是 ‎ ‎14．将八进制数123(8)转化为二进制数是1010011(2) ‎ ‎15．为参加CCTV举办的中国汉字听写大赛，某中学举行了一次大型选拔活动，随机统计了甲、乙两班各6名学生的汉字听写的成绩如图所示，设甲的众数为x, 乙的中位数为y,则x-y= 1.5 ‎ ‎16．已知函数，给出下列结论：‎ ‎①的单调递减区间；‎ ‎②当时，直线y=k与y=f （x）的图象有两个不同交点；‎ ‎③函数y=f（x）的图象与的图象没有公共点．‎ 其中正确结论的序号是 ①③ ‎ 二、解答题:(共70分)‎ ‎17.（本题10分 ）已知命题P：方程：表示焦点在y轴上的椭圆，命题q：双曲线的离心率，若“p∧q”为假命题，“p∨q”为真命题，求m的取值范围．‎ ‎【解答】解：若P真，则有9﹣m＞2m＞0即0＜m＜3‎ 若q真，则有m＞0且e2=，解得；‎ 因为p或q为真命题，P且q为假命题，则P，q一真一假．‎ ‎①若P真q假，则0＜m＜3，且m≥5或m 即0＜m，‎ ‎②若P假q真，则m≥3或m≤0且，即3≤m＜5，‎ 综上，实m的取值范围是0＜m或3≤m＜5．‎ ‎18.（12分）已知抛物线C：y2=2px（p＞0）的焦点为F（1，0），抛物线E：x2=2py的焦点为M．（1）若过点M的直线l与抛物线C有且只有一个交点，求直线l的方程；‎ ‎（2）若直线MF与抛物线C交于A、B两点，求△OAB的面积．‎ ‎【解答】解：（1）∵抛物线C：y2=2px（p＞0）的焦点为F（1，0），抛物线E：x2=2py的焦点为M，‎ ‎∴p=2，M（0，1）‎ 斜率不存在时，x=0，满足题意；‎ 斜率存在时，设方程为y=kx+1，代入y2=4x，可得k2x2+（2k﹣4）x+1=0，‎ k=0时，x=，满足题意，方程为y=1；‎ k≠0时，△=（2k﹣4）2﹣4k2=0，∴k=1，方程为y=x+1，‎ 综上，直线l的方程为x=0或y=1或y=x+1；‎ ‎（2）直线MF的方程为y=﹣x+1，代入y2=4x，可得y2+4y﹣4=0，‎ 设A（x1，y1），B（x2，y2），则y1+y2=﹣4，y1y2=﹣4，‎ ‎∴△OAB的面积S=|OF||y1﹣y2|==2．‎ ‎19．“砥砺奋进的五年”，泉州经济社会发展取得新成就.自2012年以来，泉州城乡居民收入稳步增长.随着扩大内需，促进消费等政策的出台，居民消费支出全面增长，消费结构持续优化升级，城乡居民人均可支配收入快速增长，人民生活品质不断提升.下图是泉州市2012-2016年城乡居民人均可支配收入实际增速趋势图（例如2012年，泉州城镇居民收入实际增速为7.3%，农村居民收入实际增速为8.2%）.‎ ‎ ‎ ‎（Ⅰ）从2012-2016五年中任选一年，求城镇居民收入实际增速大于7%的概率；‎ ‎（Ⅱ）从2012-2016五年中任选一年，求至少有一年农村和城镇居民收入实际增速均超过7%的概率；‎ 解：（Ⅰ）设城镇居民收入实际增速大于7%为事件A，由图可知，这五年中有2012,2013,2014这三年城镇居民收入实际增速大于7%，所以P(A)= .‎ ‎（Ⅱ）设至少有一年农村和城镇居民实际收入增速均超7%为事件B，这五年中任选两年，有(2012,2013)，(2012,2014)，(2012,2015)，(2012,2016)，(2013,2014)，(2013,2015)，(2013,2016)，(2014,2015)，(2014,2016)，(2015,2016)共10种情况，其中至少有一年农村和城镇居民实际收入增速均超过7%的为前9种情况，所以P(B)= .‎ ‎20．（本题12分 ）已知函数 ‎（1当a=2,b=1时，若方程=m的有2个实根，求m的值；‎ ‎（2）当时，若f(x)在(0，＋∞)上为增函数，求实数a的取值范围．‎ 由已知得在(0，＋∞)上恒成立 ‎21．椭圆： 的离心率为，过其右焦点与长轴垂直的直线与椭圆在第一象限相交于点， .‎ ‎（1）求椭圆的标准方程；‎ ‎（2）设椭圆的左顶点为，右顶点为，点是椭圆上的动点，且点与点， 不重合，直线与直线相交于点，直线与直线相交于点，求证：以线段为直径的圆恒过定点.‎ ‎（1）解： ，又，联立解得： ，‎ 所以椭圆C的标准方程为. ‎ ‎（2）证明：设直线AP的斜率为k，则直线AP的方程为，‎ 联立得.‎ ‎ ，‎ 整理得： ，故，‎ 又， (分别为直线PA，PB的斜率)，‎ 所以，‎ 所以直线PB的方程为： ，‎ 联立得，‎ 所以以ST为直径的圆的方程为： ，‎ 令，解得： ，‎ 所以以线段ST为直径的圆恒过定点. ‎ ‎22. （1） ，令 ，解得 ．‎ 当 变化时，， 的变化情况如表： ‎ 所以 在内是增函数，在 内是减函数．‎ 函数 在 处取得极大值 ，且 ．‎ ‎      （2） （）若 ，‎ 由（Ⅰ）及 ，得 ，与 矛盾．‎ ‎（）若 ，‎ 由（Ⅰ）及 ，得 ，与矛盾．‎ 根据（）（）得 ，不妨设 ，．‎ 由（Ⅱ）可知，，，‎ 因为 ，‎ 又由（Ⅰ）可知函数 在区间 内是增函数，‎ 所以 ，即 ．‎