- 2021-06-23 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学(理)卷·2019届江西省南昌市第二中学高二下学期第一次月考(2018-04)
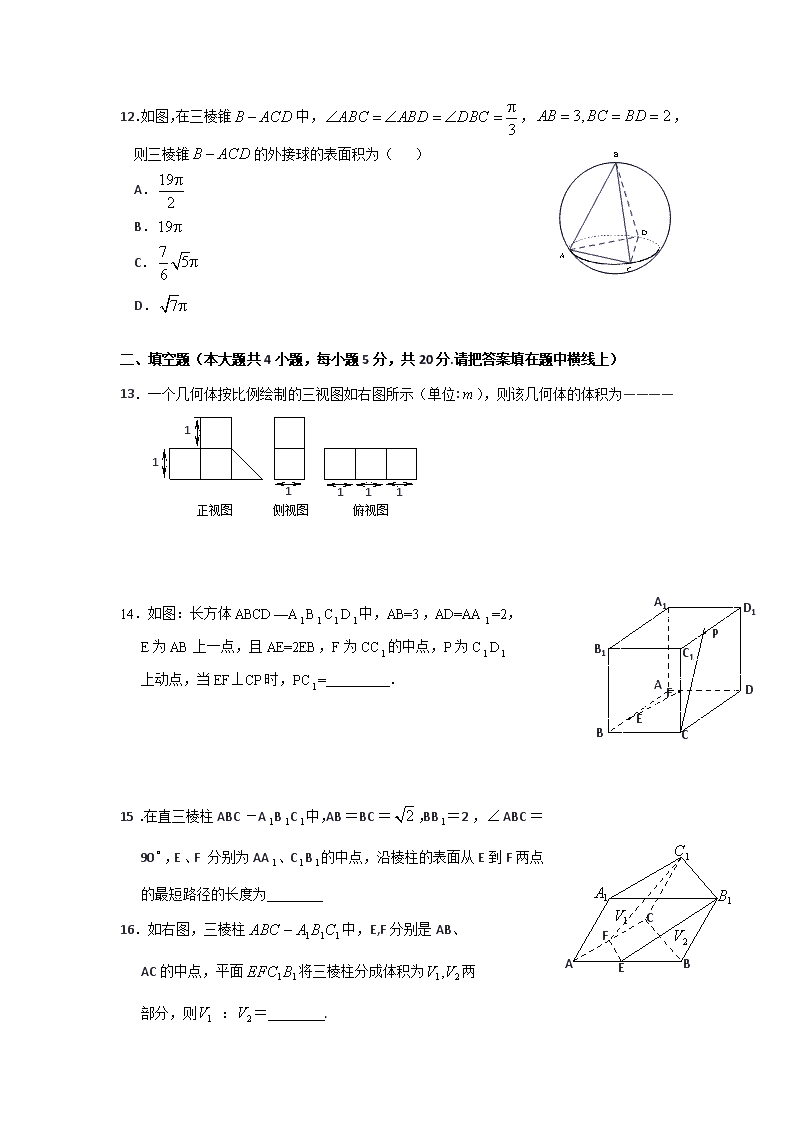
南昌二中2017-2018学年度下学期第一次月考 高二数学(理)试卷 命题人:曹开文 审题人:刘蓓蓓 满分:150分 考试时间:120分钟 一、选择题(在每小题给出的四个选项中,只有一个正确.每小题5分,共60分) 1.给出下列四个命题,其中正确的是 ( ) ①空间四点共面,则其中必有三点共线; ②空间四点不共面,则其中任何三点不共线; ③空间四点中存在三点共线,则此四点共面; ④空间四点中任何三点不共线,则此四点不共面 A.②③ B.①②③ C.①② D.②③④ 2.在空间中,下列命题正确的是( ) A.若直线//平面,直线//,则//; B.若//平面,//平面,,则// C.若,,则//; D.若//,,则//平面 3..设是三条不同的直线,是两个不同的平面,则能使成立是( ) A. B. C. D. 4.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是( ) A.6 B.8 C.2+3 D.2+2 5.已知、是异面直线,平面,平面,则、的位置关系是 ( ) A.相交 B.平行 C.重合 D.不能确定 6. 关于直线与平面,有以下四个命题: ①若且,则;②若且,则; ③若且,则;④若且,则; 其中真命题的序号是 ( ) A.①② B.③④ C.①④ D.②③ 7.在四面体中,两两垂直,且均相等,是的中点,则异面直线与所成的角为 ( ) A. B. C. D. 8.如图,各棱长均为的正三棱柱,、分别为线段 、上的动点,且 平面,则这样的有 ( ) A. 1条 B. 2条 C. 3条 D. 无数条 9.从点P引三条射线PA、PB、PC,每两条的夹角都是60,则二面角B-PA-C的余弦值是( ) A. B. C. D. 10.某几何体的三视图如图所示,若该几何体的体积为,则图 中的值为( ) A. B. C. D.[ 11.已知正三棱锥P—ABC的高PO的长为,点D为侧棱PC的中点,PO与BD所成角的余弦值为,则正三棱锥P—ABC的体积为 ( ) A. B. C. D. 12.如图,在三棱锥中,,, 则三棱锥的外接球的表面积为( ) A. B. C. D. 二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中横线上) 1 1 俯视图 1 1 1 正视图 1 侧视图 13.一个几何体按比例绘制的三视图如右图所示(单位:),则该几何体的体积为———— A B C D A1 B1 C1 D1 ·E F· ·P 14. 如图:长方体ABCD—ABCD中,AB=3,AD=AA=2, E为AB上一点,且AE=2EB,F为CC的中点,P为CD 上动点,当EF⊥CP时,PC= . A B C E F 15.在直三棱柱ABC-ABC中,AB=BC=,BB=2,ABC=90,E、F分别为AA、CB的中点,沿棱柱的表面从E到F两点的最短路径的长度为 16.如右图,三棱柱中,E,F分别是AB、 AC的中点,平面将三棱柱分成体积为两 部分,则 := . 三.解答题(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)如图四棱锥P—ABCD,底面ABCD为矩形,侧棱PA⊥底面ABCD,其中BC=2AB=2PA=6,M、N为侧棱PC上的三等分点。 (Ⅰ)证明:AN∥平面MBD;[] (Ⅱ)求三棱锥N—MBD的体积。 18.(本小题满分12分)如图是某直三棱柱被削去上底后所得几何体的左视图、俯视图、直观图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。 (Ⅰ)求该几何体的表面积和体积; A B C E D M · 4 2 2 2 左视图 俯视图 直观图 (Ⅱ)求点C到平面MAB的距离。 19.(本小题满分12分)如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点。 (Ⅰ)求异面直线NE与AM所成角的余弦值; (Ⅱ)在线段AN上是否存在一点S,使ES⊥平面AMN? 若存在,求线段AS的长;若不存在,请说明理由。 20.(本小题满分12分)如图,在斜三棱柱ABC-A1B1C1 中,侧面AA1B1B⊥底面ABC, 侧棱AA1与底面ABC成600的角, AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。E是线段BC1上一点,且BE=BC1 .[] (1)求证: GE∥侧面AA1B1B ; (2)求平面B1GE与底面ABC所成锐二面角的正切值. 21.(本小题满分12分)已知动圆过定点,且在轴上截得的弦长为4,记动圆圆心的轨迹为曲线C. (Ⅰ)求直线与曲线C围成的区域面积; (Ⅱ)点在直线上,点,过点作曲线C的切线、,切点分别为、,证明:存在常数,使得,并求的值. 22.(本小题满分12分)已知函数, . (Ⅰ)求的单调区间. (Ⅱ)证明:当时,方程在区间上只有一个零点.[] (Ⅲ)设,其中若恒成立,求的取值范围. [] 南昌二中2017-2018学年度下学期第一次月考 高二数学(理)参考答案 一.选择题:ADCBA DCDCC CA 二.填空题 13.; 14.2 15.; 16. 三.解答题 A B C E D M · N H 17.(Ⅰ)连结AC交BD于O,连结OM,∵底面ABCD为矩形,∴O为AC的中点,∵M、N为侧棱 PC上的三等分点,∴CM=MN,∴OM∥AN,∵OM平面MBD, AN平面MBD,∴AN∥平面MBD; (Ⅱ) 18.解:由题意知,EA平面ABC,DC平面ABC,AE∥DC,AE=2,DC=4, ABAC,且AC=2。 (Ⅰ)∵EA平面ABC,∴EAAB,又ABAC,∴AB平面ACDE ∴四棱锥B—ACDE的高,又梯形ACDE的面积S=6 ∴,表面积S= . A B C D M N E S x y z (Ⅱ)M到AB的距离MN=,设C到面MAB的距离为,由得: ,∴ 19.解法一:(Ⅰ)如图,以D为坐标原点,建立空间坐标系D—xyz 依题意,易得D(0,0,0),A(1,0,0),C(0,1,0),M(0,0,1),B(1,1,0),N(1,1,1), E(,1,0).∴, ∴ ∴异面直线NE与AM所成角的余弦值为 (Ⅱ)假设在AN上存在点S,使得ES⊥平面AMN,∵ 设,又 ∴ ∵⊥平面AMN,∴ 此时,∴,所以线段AN上存在点S,且当时,ES⊥平面AMN。 解法二:(Ⅰ)延长AD至F,使DF=EB,连EF,MF,BD,∵EB//DF,∴四边形DBEF为平行四边形,∴DB∥=EF,又MD⊥平面ABCD,NB⊥平面ABCD,∴MD∥NB, 又∵MD=NB,∴四边形MNEF为平行四边形。∴MF∥=BD,∴四边形MNEF为平行四边形。MF∥=NE,∴∠AMF为异面直线AM与NE所成的角或它的补角。 A B C D M N E F R S P ∴ 在△AMF中,, ∴异面直线NE与AM所成角的余弦值为 (Ⅱ)存在点S为AN的中点,使ES⊥平面AMN, 取AN的中点S,连结ES,再取AM,DC的中点R,P,连结RS,RP,EP。则EP∥=BD,RS∥=MN 又MD∥=NB,∴MNBD为平行四边形。 ∴MN∥=BD,∴EP∥=RS,∴SE∥=RP,∵,S为AN中点 ∴SE⊥AN,同理RP⊥AM,∴ES⊥AM,又AMAN=A,∴ES⊥平面AMN ∵AN=,S为AN的中点,∴。 ∴线段AN上存在点S, 使ES⊥平面AMN。此时。 20. (解法一:(1)延长B1E交BC于F, ∵ΔB1EC1∽ΔFEB, BE=EC1∴BF=B1C1=BC, 从而F为BC的中点.∵G为ΔABC的重心,∴A、G、F三点共线,且==, ∴GE∥AB1,又GE侧面AA1B1B, ∴GE∥侧面AA1B1B (2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,∵侧面AA1B1B⊥底面ABC,∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角, AA1= 2, ∴∠B1BH=600,BH=1,B1H=.在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,又平面B1GE与底面ABC的交线为AF,∴∠B1TH为所求二面角的平面角. ∴AH=AB+BH=3,∠HAT=300, ∴HT=AHsin300=, 在RtΔB1HT中,tan∠B1TH==. 解法二:向量法(略) 21:(Ⅰ)设动圆圆心的坐标为,由题意可得, ,化简得, 联立方程组,解得或,所以直线 与曲线C围成的区域面积为; (Ⅱ)设、,则由题意可得,切线的方程为,切线的方程为,再设点,从而有,所以可得出直线AB的方程为,即. 联立方程组,得,又,所以有, 可得, , , 所以常数. 22解析()由已知,令,则,令, 则,故的单调减区间为,单调增区间为. ()设, ,则, 由()可知在,上单调递增,且, , ∴在上只有个零点,故当,方程在区间上只有一个零点. (), , 的定义域是, ,令,则, 由()得,在区间上只有一个零点,且是增函数,不妨设的零点是, 则当时, ,即, 单调递减. 当时, ,即, 单调递增, ∴函数的最小值为 , 由,得,故, 根据题意,即,解得,故实数的取值范围是.查看更多