数学卷·2018届江西省上饶市上饶县中学高二下学期第一次月考数学试卷（理零） （解析版）

数学卷·2018届江西省上饶市上饶县中学高二下学期第一次月考数学试卷（理零） （解析版）

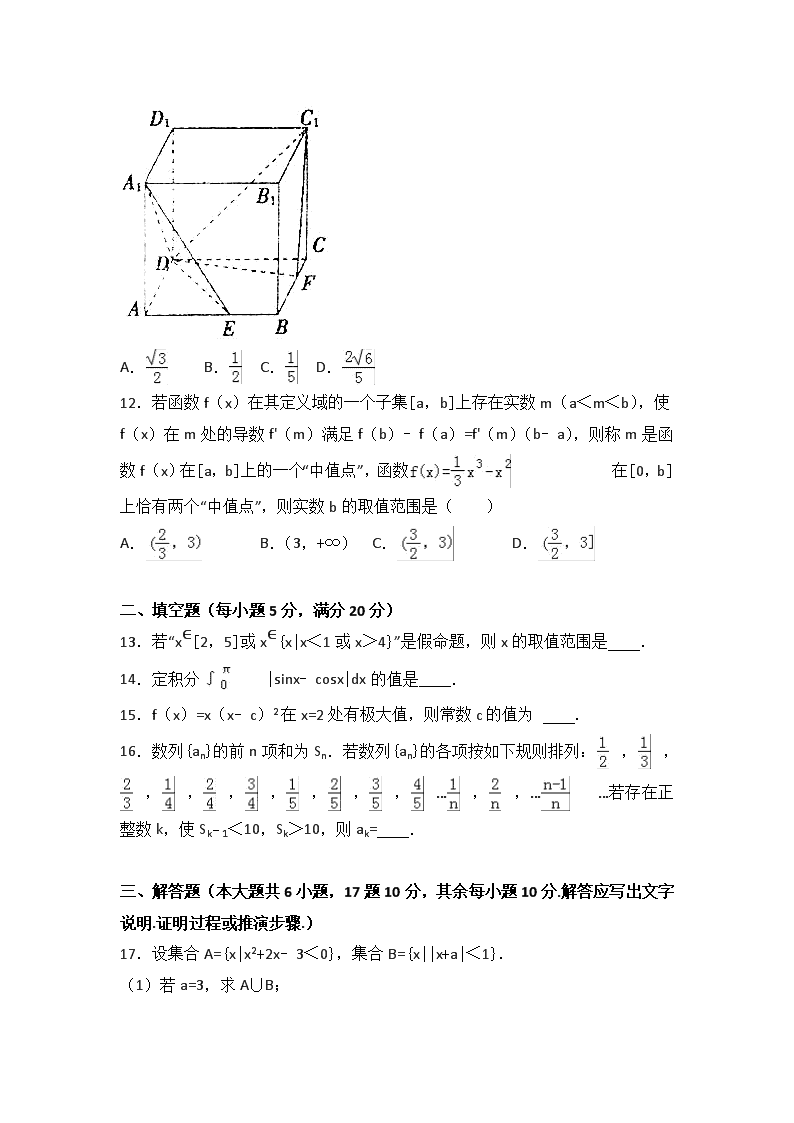
‎2016-2017学年江西省上饶市上饶县中学高二（下）第一次月考数学试卷（理零）‎ ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．命题“若q则p”的否命题是（　　）‎ A．若q则￢p B．若￢q则p C．若￢q则￢p D．若￢p则￢q ‎2．已知i是虚数单位，复数对应的点在第（　　）象限．‎ A．一 B．二 C．三 D．四 ‎3．已知m、n为两条不同直线，α、β为两个不同平面，则下列命题中正确的是（　　）‎ A．m∥n，m⊥α⇒n⊥α B．α∥β，m⊂α，n⊂β⇒m∥n C．m⊥α，m⊥n⇒n∥α D．m⊂α，n⊂α，m∥β，n∥β⇒α∥β ‎4．中国有个名句“运筹帷幄之中，决胜千里之外．”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图所示），表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推．例如6613用算筹表示就是，则9117用算筹可表示为（　　）‎ A． B． C． D．‎ ‎5．“直线（m+2）x+3my+1=0与（m﹣2）x+（m+2）y=0互相垂直”是“”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎6．已知y=f（x）的导函数为y=f'（x），且在x=1处的切线方程为y=﹣x+‎ ‎3，则f（1）﹣f'（1）=（　　）‎ A．2 B．3 C．4 D．5‎ ‎7．某个命题与正整数n有关，如果当n=k（k∈N+）时命题成立，那么可推得当n=k+1时命题也成立． 现已知当n=7时该命题不成立，那么可推得（　　）‎ A．当n=6时该命题不成立 B．当n=6时该命题成立 C．当n=8时该命题不成立 D．当n=8时该命题成立 ‎8．直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为（　　）‎ A．4 B．4 C．2 D．2‎ ‎9．空间四边形ABCD中，若向量=（﹣3，5，2），=（﹣7，﹣1，﹣4）点E，F分别为线段BC，AD的中点，则的坐标为（　　）‎ A．（2，3，3） B．（﹣2，﹣3，﹣3） C．（5，﹣2，1） D．（﹣5，2，﹣1）‎ ‎10．设f′（x）是函数f（x）的导函数，将y=f（x）和y=f′（x）的图象画在同一个直角坐标系中，不可能正确的是（　　）‎ A． B． C． D．‎ ‎11．如图所示，ABCD﹣A1B1C1D1是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE=BF．当A1，E，F，C1共面时，平面A1DE与平面C1DF所成锐二面角的余弦值为（　　）‎ A． B． C． D．‎ ‎12．若函数f（x）在其定义域的一个子集[a，b]上存在实数m（a＜m＜b），使f（x）在m处的导数f'（m）满足f（b）﹣f（a）=f'（m）（b﹣a），则称m是函数f（x）在[a，b]上的一个“中值点”，函数在[0，b]上恰有两个“中值点”，则实数b的取值范围是（　　）‎ A． B．（3，+∞） C． D．‎ ‎　‎ 二、填空题（每小题5分，满分20分）‎ ‎13．若“x∈[2，5]或x∈{x|x＜1或x＞4}”是假命题，则x的取值范围是　　．‎ ‎14．定积分|sinx﹣cosx|dx的值是　　．‎ ‎15．f（x）=x（x﹣c）2在x=2处有极大值，则常数c的值为 　　．‎ ‎16．数列{an}的前n项和为Sn．若数列{an}的各项按如下规则排列：，，，，，，，，，…，，……若存在正整数k，使Sk﹣1＜10，Sk＞10，则ak=　　．‎ ‎　‎ 三、解答题（本大题共6小题，17题10分，其余每小题10分.解答应写出文字说明.证明过程或推演步骤.）‎ ‎17．设集合A={x|x2+2x﹣3＜0}，集合B={x||x+a|＜1}．‎ ‎（1）若a=3，求A∪B；‎ ‎（2）设命题p：x∈A，命题q：x∈B，若p是q成立的必要不充分条件，求实数a的取值范围．‎ ‎18．已知命题p：方程表示焦点在y轴上的椭圆，命题q：关于x的方程x2+2mx+2m+3=0无实根，若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．‎ ‎19．已知f（x）=ax4+bx2+c的图象经过点（0，1），且在x=1处的切线方程是y=x﹣2‎ ‎（Ⅰ）求实数a，b，c的值；‎ ‎（Ⅱ）求y=f（x）的单调递增区间．‎ ‎20．如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点，在五棱锥P﹣ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H．‎ ‎（1）求证：AB∥FG；‎ ‎（2）若PA⊥底面ABCDE，且PA=AE，求直线BC与平面ABF所成角的大小，并求线段PH的长．‎ ‎21．已知椭圆C的中心在原点，焦点在x轴上，焦距为2，离心率为 ‎（1）求椭圆C的方程；‎ ‎（2）设直线l经过点M（0，1），且与椭圆C交于A，B两点，若=2，求直线l的方程．‎ ‎22．已知函数f（x）=alnx+x2（a为实常数）．‎ ‎（1）当a=﹣4时，求函数f（x）在[1，e]上的最大值及相应的x值；‎ ‎（2）当x∈[1，e]时，讨论方程f（x）=0根的个数．‎ ‎（3）若a＞0，且对任意的x1，x2∈[1，e]，都有，求实数a的取值范围．‎ ‎　‎ ‎2016-2017学年江西省上饶市上饶县中学高二（下）第一次月考数学试卷（理零）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．命题“若q则p”的否命题是（　　）‎ A．若q则￢p B．若￢q则p C．若￢q则￢p D．若￢p则￢q ‎【考点】四种命题间的逆否关系．‎ ‎【分析】根据否命题的定义进行判断即可．‎ ‎【解答】解：根据否命题的定义，同时否定原命题的条件和结论即可得到命题的否命题．‎ ‎∴命题“若q则p”的否命题是的否命题是：若￢q则￢p．‎ 故选：C．‎ ‎　‎ ‎2．已知i是虚数单位，复数对应的点在第（　　）象限．‎ A．一 B．二 C．三 D．四 ‎【考点】复数代数形式的乘除运算．‎ ‎【分析】利用复数的运算法则、几何意义即可得出．‎ ‎【解答】解：复数===2﹣i对应的点（2，﹣1）在第四象限．‎ 故选：D．‎ ‎　‎ ‎3．已知m、n为两条不同直线，α、β为两个不同平面，则下列命题中正确的是（　　）‎ A．m∥n，m⊥α⇒n⊥α B．α∥β，m⊂α，n⊂β⇒m∥n C．m⊥α，m⊥n⇒n∥α D．m⊂α，n⊂α，m∥β，n∥β⇒α∥β ‎【考点】命题的真假判断与应用．‎ ‎【分析】由线面垂直的几何特征，及线面垂直的第二判定定理，可判断A的真假；‎ 根据面面平行的几何特征及线线位置关系的定义，可判断B的真假；‎ 根据线面垂直及线线垂直的几何特征，及线面平行的判定方法，可判断C的真假；‎ 根据面面平行的判定定理，可以判断D的真假．‎ ‎【解答】解：若m∥n，m⊥α根据线面垂直的第二判定定理可得n⊥α，故A正确；‎ 若α∥β，m⊂α，n⊂β，则m∥n或m，n异面，故B错误；‎ 若m⊥α，m⊥n，则n∥α或n⊂α，故C错误；‎ 由m⊂α，n⊂α，m∥β，n∥β，若a，b相交，则可得α∥β，若a∥b，则α与β可能平行也可能相交，故D错误；‎ 故选A ‎　‎ ‎4．中国有个名句“运筹帷幄之中，决胜千里之外．”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图所示），表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推．例如6613用算筹表示就是，则9117用算筹可表示为（　　）‎ A． B． C． D．‎ ‎【考点】进行简单的合情推理．‎ ‎【分析】根据新定义直接判断即可 ‎【解答】解：由题意各位数码的筹式需要纵横相间，‎ 个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，‎ 则9117 用算筹可表示为，‎ 故选：C ‎　‎ ‎5．“直线（m+2）x+3my+1=0与（m﹣2）x+（m+2）y=0互相垂直”是“”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【考点】直线的一般式方程与直线的垂直关系．‎ ‎【分析】由直线（m+2）x+3my+1=0与（m﹣2）x+（m+2）y=0互相垂直，借助于系数间的关系求得m的值，再把代入两直线方程判断是否垂直得答案．‎ ‎【解答】解：若直线（m+2）x+3my+1=0与（m﹣2）x+（m+2）y=0互相垂直，‎ 则（m+2）（m﹣2）+3m（m+2）=0，解得：m=﹣2，m=．‎ 由，则直线（m+2）x+3my+1=0化为5x+3y+2=0，斜率为．‎ 直线（m﹣2）x+（m+2）y=0化为﹣3x+5y=0，斜率为．‎ 由，得直线（m+2）x+3my+1=0与（m﹣2）x+（m+2）y=0互相垂直．‎ ‎∴“直线（m+2）x+3my+1=0与（m﹣2）x+（m+2）y=0互相垂直”是“”的必要不充分条件．‎ 故选：B．‎ ‎　‎ ‎6．已知y=f（x）的导函数为y=f'（x），且在x=1处的切线方程为y=﹣x+3，则f（1）﹣f'（1）=（　　）‎ A．2 B．3 C．4 D．5‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】由已知切线的方程，结合导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，计算即可得到所求值．‎ ‎【解答】解：由f（x）在x=1处的切线方程为y=﹣x+3，‎ 可得则f（1）﹣f'（1）=3﹣1﹣（﹣1）=3．‎ 故选：B．‎ ‎　‎ ‎7．某个命题与正整数n有关，如果当n=k（k∈N+）时命题成立，那么可推得当n=k+1时命题也成立． 现已知当n=7时该命题不成立，那么可推得（　　）‎ A．当n=6时该命题不成立 B．当n=6时该命题成立 C．当n=8时该命题不成立 D．当n=8时该命题成立 ‎【考点】数学归纳法．‎ ‎【分析】本题考查的知识点是数学归纳法，由归纳法的性质，我们由P（n）对n=k成立，则它对n=k+1也成立，由此类推，对n＞k的任意整数均成立，结合逆否命题同真同假的原理，当P（n）对n=k不成立时，则它对n=k﹣1也不成立，由此类推，对n＜k的任意正整数均不成立，由此不难得到答案．‎ ‎【解答】解：由题意可知，原命题成立则逆否命题成立，‎ P（n）对n=7不成立，P（n）对n=6也不成立，‎ 否则n=6时，由由已知推得n=7也成立．‎ 与当n=7时该命题不成立矛盾 故选A．‎ ‎　‎ ‎8．直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为（　　）‎ A．4 B．4 C．2 D．2‎ ‎【考点】定积分在求面积中的应用．‎ ‎【分析】由题意首先求出第一象限的交点，然后利用定积分表示围成的图形的面积，然后计算即可．‎ ‎【解答】解：先根据题意画出图形，两个图形在第一象限的交点为（2，8），‎ 所以曲线y=x3与直线y=4x在第一象限所围成的图形的面积是∫02（4x﹣x3）dx，‎ 而∫02（4x﹣x3）dx=（2x2﹣x4）|02=8﹣4=4‎ ‎∴曲封闭图形的面积是4，‎ 故选B．‎ ‎　‎ ‎9．空间四边形ABCD中，若向量=（﹣3，5，2），=（﹣7，﹣1，﹣4）点E，F分别为线段BC，AD的中点，则的坐标为（　　）‎ A．（2，3，3） B．（﹣2，﹣3，﹣3） C．（5，﹣2，1） D．（﹣5，2，﹣1）‎ ‎【考点】空间向量的概念．‎ ‎【分析】点E，F分别为线段BC，AD的中点，可得=，， =．代入计算即可得出．‎ ‎【解答】解：∵点E，F分别为线段BC，AD的中点，‎ ‎∴=，， =．‎ ‎∴=﹣‎ ‎=‎ ‎= [（3，﹣5，﹣2）+（﹣7，﹣1，﹣4）]‎ ‎=‎ ‎=（﹣2，﹣3，﹣3）．‎ 故选：B．‎ ‎　‎ ‎10．设f′（x）是函数f（x）的导函数，将y=f（x）和y=f′（x）的图象画在同一个直角坐标系中，不可能正确的是（　　）‎ A． B． C． D．‎ ‎【考点】导数的运算；函数的图象．‎ ‎【分析】利用导数与函数单调性的关系即可得出．‎ ‎【解答】解：因为把上面的作为函数：在最左边单调递增，其导数应为大于0，但是其导函数的值小于0，故不正确；‎ 同样把下面的作为函数，中间一段是减函数，导函数应该小于0，也不正确．因此D不正确．‎ 故选：D．‎ ‎　‎ ‎11．如图所示，ABCD﹣A1B1C1D1是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE=BF．当A1，E，F，C1共面时，平面A1DE与平面C1DF所成锐二面角的余弦值为（　　）‎ A． B． C． D．‎ ‎【考点】二面角的平面角及求法．‎ ‎【分析】以D为原点，DA，DC，DD 1 所在直线分别为x轴、y轴、z轴建立空间直角坐标系，由题意知：当E（6，3，0），F（3，6，0）时，A 1，E，F、C 1 共面，由此利用向量法能求出平面A1DE与平面C1DF所成锐二面角的余弦值．‎ ‎【解答】解：以D为原点，DA，DC，DD1 所在直线分别为x轴、y轴、z轴建立空间直角坐标系，‎ 由题意知：当E（6，3，0），F（3，6，0）时，A1，E，F、C1 共面，‎ 设平面A1 DE的法向量为=（a，b，c），‎ ‎=（6，0，6），=（6，3，0），A1（6，06），D（0，0，0），C1（0，6，6），‎ 则，取a=1，得=（1，﹣2，﹣1），‎ 设平面C1 DF的一个法向量为=（x，y，z），‎ ‎=（0，6，6），=（3，6，0），‎ 则，取x=2，得=（2，﹣1，1），‎ 设平面A1DE与平面C1DF所成锐二面角为θ，‎ 则cosθ===，‎ ‎∴平面A1DE与平面C1DF所成锐二面角的余弦值为．‎ 故选：B．‎ ‎　‎ ‎12．若函数f（x）在其定义域的一个子集[a，b]上存在实数m（a＜m＜b），使f（x）在m处的导数f'（m）满足f（b）﹣f（a）=f'（m）（b﹣a），则称m是函数f（x）在[a，b]上的一个“中值点”，函数在[0，b]上恰有两个“中值点”，则实数b的取值范围是（　　）‎ A． B．（3，+∞） C． D．‎ ‎【考点】导数的运算．‎ ‎【分析】根据新定义得到x1，x2为方程x2﹣2x﹣b2+b=0在（0，b）上有两个不同根，构造函数g（x）=x2﹣2x﹣b2+b，列出不等式组，解得即可 ‎【解答】解：f′（x）=x2﹣2x，‎ 设=b2﹣b，‎ 由已知可得x1，x2为方程x2﹣2x﹣b2+b=0在（0，b）上有两个不同根，‎ 令g（x）=x2﹣2x﹣b2+b，‎ 则，‎ 解得＜b＜3，‎ 故选：C ‎　‎ 二、填空题（每小题5分，满分20分）‎ ‎13．若“x∈[2，5]或x∈{x|x＜1或x＞4}”是假命题，则x的取值范围是　[1，2）　．‎ ‎【考点】元素与集合关系的判断；四种命题的真假关系．‎ ‎【分析】原命题是假命题可转化成它的否命题是真命题进行求解，求出满足条件的x即可．‎ ‎【解答】解：若“x∈[2，5]或x∈{x|x＜1或x＞4}”是假命题 则它的否命题为真命题即{x|x＜2或x＞5}且{x|1≤x≤4}是真命题 所以的取值范围是[1，2），‎ 故答案为[1，2）．‎ ‎　‎ ‎14．定积分|sinx﹣cosx|dx的值是　2　．‎ ‎【考点】定积分．‎ ‎【分析】由题意可得|sinx﹣cosx|dx=（cosx﹣sinx）dx+（sinx﹣cosx）dx，再根据定积分的计算法则计算即可．‎ ‎【解答】解： |sinx﹣cosx|dx=（cosx﹣sinx）dx+（sinx﹣cosx）dx，‎ ‎=（sinx+cosx）|+（﹣cosx﹣sinx）|，‎ ‎=[（sin+cos）﹣（sin0+cos0）]﹣[（sinπ+cosπ﹣（sin+cos）]，‎ ‎=（﹣1）﹣（﹣1﹣），‎ ‎=2，‎ 故答案为：2．‎ ‎　‎ ‎15．f（x）=x（x﹣c）2在x=2处有极大值，则常数c的值为 　6　．‎ ‎【考点】利用导数研究函数的极值．‎ ‎【分析】先求出f′（x），根据f（x）在x=2处有极大值则有f′（2）=0得到c的值为2或6，先让c=2然后利用导数求出函数的单调区间，从而得到x=2取到极小值矛盾，所以舍去，所以得到c的值即可．‎ ‎【解答】解：f（x）=x3﹣2cx2+c2x，f′（x）=3x2﹣4cx+c2，‎ f′（2）=0⇒c=2或c=6．若c=2，f′（x）=3x2﹣8x+4，‎ 令f′（x）＞0⇒x＜或x＞2，f′（x）＜0⇒＜x＜2，‎ 故函数在（﹣∝，）及（2，+∞）上单调递增，在（，2）上单调递减，‎ ‎∴x=2是极小值点．故c=2不合题意，c=6．‎ 故答案为6‎ ‎　‎ ‎16．数列{an}的前n项和为Sn．若数列{an}的各项按如下规则排列：，，，，，，，，，…，，……若存在正整数k，使Sk﹣1＜10，Sk＞10，则ak=　　．‎ ‎【考点】归纳推理．‎ ‎【分析】把原数列划分，发现他们的个数是1，2，3，4，5…构建新数列bn，很显然是个等差数列，利用等差数列的和知道T5=，T6=，所以ak定在，，…，中，在根据Sk﹣1＜10，Sk≥10求出具体结果．‎ ‎【解答】解：把原数列分组，分母相同的为一组，发现他们的个数是1，2，3，4，5…‎ 构建新数列{bn}，表示数列中每一组的和，则bn=是个等差数列，记{bn}的前n项和为Tn，‎ 利用等差数列的和知道T5=，T6=，‎ 所以ak定在，，…，中，‎ 又因为Sk﹣1＜10，Sk≥10，而T5+++…+=9+＜10，T5+++…++=10+＞10，‎ 故第k项为ak=．‎ 故答案为．‎ ‎　‎ 三、解答题（本大题共6小题，17题10分，其余每小题10分.解答应写出文字说明.证明过程或推演步骤.）‎ ‎17．设集合A={x|x2+2x﹣3＜0}，集合B={x||x+a|＜1}．‎ ‎（1）若a=3，求A∪B；‎ ‎（2）设命题p：x∈A，命题q：x∈B，若p是q成立的必要不充分条件，求实数a的取值范围．‎ ‎【考点】必要条件、充分条件与充要条件的判断；并集及其运算．‎ ‎【分析】（1）通过解不等式，求出集合A、B，从而求出其并集即可；（2）问题转化为集合B是集合A的真子集，得到关于a的不等式组，解出即可．‎ ‎【解答】解：（1）解不等式x2+2x﹣3＜0，‎ 得﹣3＜x＜1，即A=（﹣3，1），…‎ 当a=3时，由|x+3|＜1，‎ 解得﹣4＜x＜﹣2，即集合B=（﹣4，﹣2），…‎ 所以A∪B=（﹣4，1）；…‎ ‎（2）因为p是q成立的必要不充分条件，‎ 所以集合B是集合A的真子集…‎ 又集合A=（﹣3，1），B=（﹣a﹣1，﹣a+1），…‎ 所以或，…‎ 解得0≤a≤2，‎ 即实数a的取值范围是0≤a≤2…‎ ‎　‎ ‎18．已知命题p：方程表示焦点在y轴上的椭圆，命题q：关于x的方程x2+2mx+2m+3=0无实根，若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】若“p∧q”为假命题，“p∨q”为真命题，则p，q为一个真命题，一个假命题，进而可得实数m的取值范围．‎ ‎【解答】解：∵方程表示焦点在y轴上的椭圆，‎ ‎∴0＜m+1＜3﹣m，‎ 解得：﹣1＜m＜1，‎ ‎∴若命题p为真命题，求实数m的取值范围是（﹣1，1）；‎ 若关于x的方程x2+2mx+2m+3=0无实根，则判别式△=4m2﹣4（2m+3）＜0，‎ 即m2﹣2m﹣3＜0，得﹣1＜m＜3．‎ 若“p∧q”为假命题，“p∨q”为真命题，则p，q为一个真命题，一个假命题，‎ 若p真q假，则，此时无解，‎ 柔p假q真，则，得1≤m＜3．‎ 综上，实数m的取值范围是[1，3）．‎ ‎　‎ ‎19．已知f（x）=ax4+bx2+c的图象经过点（0，1），且在x=1处的切线方程是y=x﹣2‎ ‎（Ⅰ）求实数a，b，c的值；‎ ‎（Ⅱ）求y=f（x）的单调递增区间．‎ ‎【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．‎ ‎【分析】（Ⅰ）求出函数的导数，根据函数的切线方程，得到关于a，b，c的方程，解出即可；‎ ‎（Ⅱ）求出函数的导数，解关于导函数的不等式，求出函数的递增区间即可．‎ ‎【解答】解：（Ⅰ）f（x）=ax4+bx2+c的图象经过点（0，1），则c=1，‎ f′（x）=4ax3+2bx，k=f′（1）=4a+2b=1，‎ 切点为（1，﹣1），则f（x）=ax4+bx2+c的图象经过点（1，﹣1）‎ 得；‎ ‎（Ⅱ）由（Ⅰ）得：，‎ 令，‎ 故函数的单调递增区间为和．‎ ‎　‎ ‎20．如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点，在五棱锥P﹣ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H．‎ ‎（1）求证：AB∥FG；‎ ‎（2）若PA⊥‎ 底面ABCDE，且PA=AE，求直线BC与平面ABF所成角的大小，并求线段PH的长．‎ ‎【考点】直线与平面所成的角．‎ ‎【分析】（1）运用线面平行的判定定理和性质定理即可证得；‎ ‎（2）由于PA⊥底面ABCDE，底面AMDE为正方形，建立如图的空间直角坐标系Axyz，分别求出A，B，C，E，P，F，及向量BC的坐标，设平面ABF的法向量为n=（x，y，z），求出一个值，设直线BC与平面ABF所成的角为α，运用sinα=|cos|，求出角α；设H（u，v，w），再设，用λ表示H的坐标，再由n=0，求出λ和H的坐标，再运用空间两点的距离公式求出PH的长．‎ ‎【解答】（1）证明：在正方形AMDE中，∵B是AM的中点，‎ ‎∴AB∥DE，又∵AB⊄平面PDE，∴AB∥平面PDE，‎ ‎∵AB⊂平面ABF，且平面ABF∩平面PDE=FG，‎ ‎∴AB∥FG；‎ ‎（2）解：∵PA⊥底面ABCDE，∴PA⊥AB，PA⊥AE，‎ 如图建立空间直角坐标系Axyz，则A（0，0，0），‎ B（1，0，0），C（2，1，0），P（0，0，2），‎ E（0，2，0），F（0，1，1），，‎ 设平面ABF的法向量为=（x，y，z），则 即，‎ 令z=1，则y=﹣1，∴ =（0，﹣1，1），‎ 设直线BC与平面ABF所成的角为α，则 sinα=|cos＜，＞|=||=，‎ ‎∴直线BC与平面ABF所成的角为，‎ 设H（u，v，w），∵H在棱PC上，∴可设，‎ 即（u，v，w﹣2）=λ（2，1，﹣2），∴u=2λ，v=λ，w=2﹣2λ，∵是平面ABF的法向量，‎ ‎∴=0，即（0，﹣1，1）•（2λ，λ，2﹣2λ）=0，解得λ=，∴H（），‎ ‎∴PH==2．‎ ‎　‎ ‎21．已知椭圆C的中心在原点，焦点在x轴上，焦距为2，离心率为 ‎（1）求椭圆C的方程；‎ ‎（2）设直线l经过点M（0，1），且与椭圆C交于A，B两点，若=2，求直线l的方程．‎ ‎【考点】直线与圆锥曲线的综合问题．‎ ‎【分析】（1）根据椭圆的焦距为2，离心率为，求出a，b，即可求椭圆C的方程；‎ ‎（2）设直线l方程为y=kx+1，代入椭圆方程，由=2得x1=﹣2x2，利用韦达定理，化简可得，求出k，即可求直线l的方程．‎ ‎【解答】解：（1）设椭圆方程为，‎ 因为，所以，‎ 所求椭圆方程为…‎ ‎（2）由题得直线l的斜率存在，设直线l方程为y=kx+1‎ 则由得（3+4k2）x2+8kx﹣8=0，且△＞0．‎ 设A（x1，y1），B（x2，y2），则由=2得x1=﹣2x2…..‎ 又，‎ 所以消去x2得 解得 所以直线l的方程为，即x﹣2y+2=0或x+2y﹣2=0…‎ ‎　‎ ‎22．已知函数f（x）=alnx+x2（a为实常数）．‎ ‎（1）当a=﹣4时，求函数f（x）在[1，e]上的最大值及相应的x值；‎ ‎（2）当x∈[1，e]时，讨论方程f（x）=0根的个数．‎ ‎（3）若a＞0，且对任意的x1，x2∈[1，e]，都有，求实数a的取值范围．‎ ‎【考点】利用导数求闭区间上函数的最值；根的存在性及根的个数判断；不等式的证明．‎ ‎【分析】（1）把a=﹣4代入函数解析式，求出函数的导函数，由导函数的零点把给出的定义[1，e]分段，判出在各段内的单调性，从而求出函数在[1，e]上的最大值及相应的x值；‎ ‎（2）把原函数f（x）=alnx+x2求导，分a≥0和a＜0讨论打哦函数的单调性，特别是当a＜0时，求出函数f（x）在[1，e]上的最小值及端点处的函数值，然后根据最小值和F（e）的值的符号讨论在x∈[1，e]时，方程f（x）=0根的个数；‎ ‎（3）a＞0判出函数f（x）=alnx+x2在[1，e]上为增函数，在规定x1＜x2后把转化为f（x2）+＜f（x1）+，构造辅助函数G（x）=f（x）+，由该辅助函数是减函数得其导函数小于等于0恒成立，分离a后利用函数单调性求a的范围．‎ ‎【解答】解：（1）当a=﹣4时，f（x）=﹣4lnx+x2，函数的定义域为（0，+∞）．‎ ‎．‎ 当x∈时，f′（x）0，‎ 所以函数f（x）在上为减函数，在上为增函数，‎ 由f（1）=﹣4ln1+12=1，f（e）=﹣4lne+e2=e2﹣4，‎ 所以函数f（x）在[1，e]上的最大值为e2﹣4，相应的x值为e；‎ ‎（2）由f（x）=alnx+x2，得．‎ 若a≥0，则在[1，e]上f′（x）＞0，函数f（x）=alnx+x2在[1，e]上为增函数，‎ 由f（1）=1＞0知，方程f（x）=0的根的个数是0；‎ 若a＜0，由f′（x）=0，得x=（舍），或x=．‎ 若，即﹣2≤a＜0，f（x）=alnx+x2在[1，e]上为增函数，‎ 由f（1）=1＞0知，方程f（x）=0的根的个数是0；‎ 若，即a≤﹣2e2，f（x）=alnx+x2在[1，e]上为减函数，‎ 由f（1）=1，f（e）=alne+e2=e2+a≤﹣e2＜0，‎ 所以方程f（x）=0在[1，e]上有1个实数根；‎ 若，即﹣2e2＜a＜﹣2，‎ f（x）在上为减函数，在上为增函数，‎ 由f（1）=1＞0，f（e）=e2+a．‎ ‎=．‎ 当，即﹣2e＜a＜﹣2时，，方程f（x）=0在[1，e]上的根的个数是0．‎ 当a=﹣2e时，方程f（x）=0在[1，e]上的根的个数是1．‎ 当﹣e2≤a＜﹣2e时，，f（e）=a+e2≥0，方程f（x）=0在[1，e]上的根的个数是2．‎ 当﹣2e2＜a＜﹣e2时，，f（e）=a+e2＜0，方程f（x）=0在[1，e]上的根的个数是1；‎ ‎（3）若a＞0，由（2）知函数f（x）=alnx+x2在[1，e]上为增函数，‎ 不妨设x1＜x2，则变为f（x2）+＜f（x1）+，由此说明函数G（x）=f（x）+在[1，e]单调递减，所以G′（x）=≤0对x∈[1，e]恒成立，即a对x∈[1，e]恒成立，‎ 而在[1，e]单调递减，所以a．‎ 所以，满足a＞0，且对任意的x1，x2∈[1，e]，都有 成立的实数a的取值范围不存在．‎