数学文卷·2018届福建省长乐高级中学高二下学期期末考试（2017-07）

数学文卷·2018届福建省长乐高级中学高二下学期期末考试（2017-07）

长乐高级中学 2016-2017 学年第二学期期末考 高二数学（文科）试卷 命题人：林经 审核人：陈振基 命题内容：集合至数列 班级 姓名 座号 成绩 说明：1、考试时间：120 分钟 满分：150 分 2、Ⅰ卷的答案用 2B 铅笔填涂到答题卡上；Ⅱ卷的答案有黑色签字笔填写在答题卡上。 一，选择题：（本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只 有一项是符合题目要求的．） 1．命题“ ， ”的否定是（ ） A． ， B． ， C． ， D． ， 2．已知集合 ， ，则 为( ) A． B． C． D． 3．复数 等于( ) A． B． C． D． 4．条件 “ ”，条件 “ ”，则 是 的( ) A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 5．函数 f(x)＝ 3x2 1－x＋lg(3x＋1)的定义域是(　　) A.(－ 1 3，＋∞) 　B.(－ 1 3，1) C.(－ 1 3， 1 3) D.(－∞，－ 1 3) 6.设函数 , ( ) （A）3 （B）6 （C）9 （D）12 7．已知两个单位向量 的夹角为 ,满足 ,实数 的值是( ) A． B． C． D． 8.在 中，已知 ， ， ，则 等于( ) A． B． C． D． 或 9.要得到函数 的图象，只需将函数 的图像 2 1 1 log (2 ), 1, ( ) 2 , 1,x x x f x x− + − <=  ≥ 2( 2) (log 12)f f− + = x R∃ ∈ 2 2 1 0x x− + < x R∃ ∈ 2 2 1 0x x− + ≥ x R∃ ∈ 2 2 1 0x x− + > x R∀ ∈ 2 2 1 0x x− + ≥ x R∀ ∈ 2 2 1 0x x− + < { }3,2,1=A { }2 2 0,B x x x x= − − = ∈R A B ∅ { }1 { }2 { }2,1 i1 i3 + + i21+ i21− i2 − i2 + :P 1x < :q ( )( )2 1 0x x+ − < P q 1 2,e e 45° ( )1 2 1 λ⊥ −e e e λ 1 2 2 3 3 2 ABC∆ 5 2a = 10c = o30A = B o105 o60 o15 o105 o15 sin(4 )3y x π= − sin 4y x= (A)向左平移 个单位 (B) 向右平移 个单位 (C)向左平移 个单位 (D) 向右平移 个单位 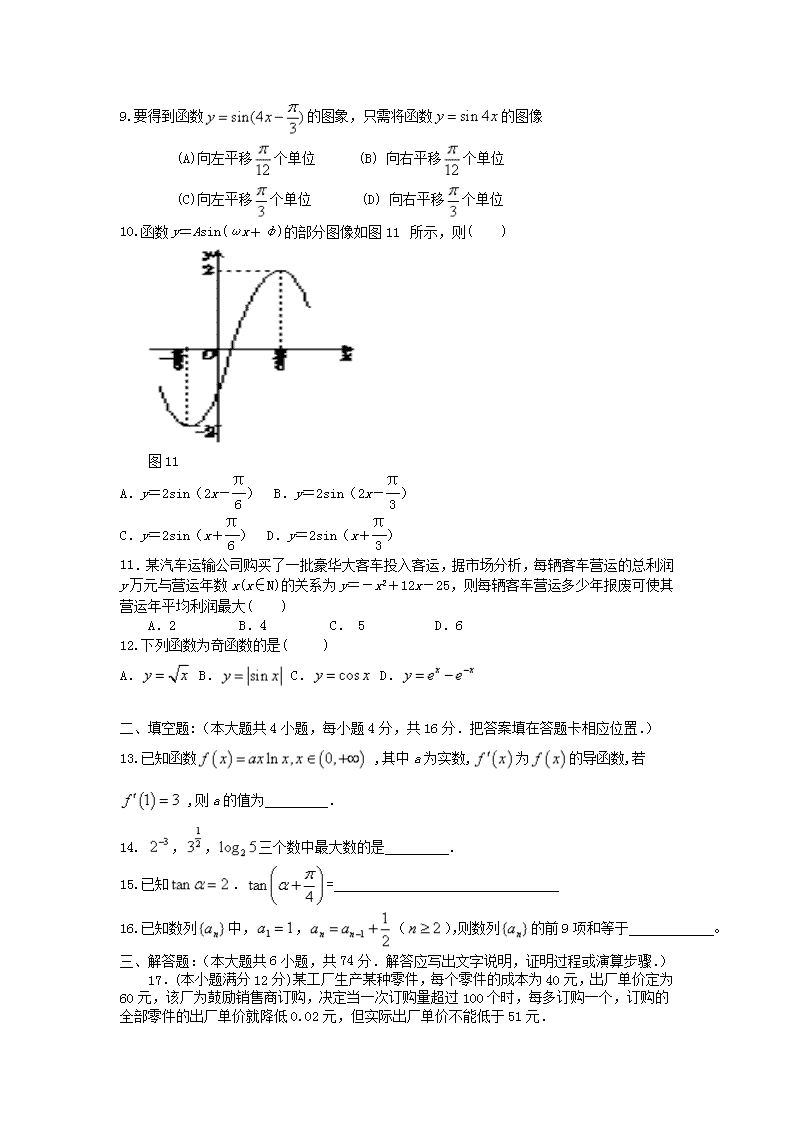10.函数 y＝Asin(ωx＋φ)的部分图像如图 1­1 所示，则(　　) 图 1­1 A．y＝2sin（2x－ π 6 ） B．y＝2sin（2x－ π 3 ） C．y＝2sin（x＋ π 6 ） D．y＝2sin（x＋ π 3 ） 11．某汽车运输公司购买了一批豪华大客车投入客运，据市场分析，每辆客车营运的总利润 y 万元与营运年数 x(x∈N)的关系为 y＝－x2＋12x－25，则每辆客车营运多少年报废可使其 营运年平均利润最大(　　) A．2　　　　 B．4　　　　 C． 5　　　　　D．6 12.下列函数为奇函数的是( ) A． B． C． D． 二、填空题:（本大题共 4 小题，每小题 4 分，共 16 分．把答案填在答题卡相应位置．） 13.已知函数 ,其中 a 为实数, 为 的导函数,若 ,则 a 的值为 ． 14. ， ， 三个数中最大数的是 ． 15.已知 ． = 16.已知数列 中， ， （ ），则数列 的前 9 项和等于 。 三、解答题：（本大题共 6 小题，共 74 分．解答应写出文字说明，证明过程或演算步骤．） 17．(本小题满分 12 分)某工厂生产某种零件，每个零件的成本为 40 元，出厂单价定为 60 元，该厂为鼓励销售商订购，决定当一次订购量超过 100 个时，每多订购一个，订购的 全部零件的出厂单价就降低 0.02 元，但实际出厂单价不能低于 51 元． (1)当一次订购量为多少时，零件的实际出厂单价恰为 51 元； (2)设一次订购量为 x 个，零件的实际出厂单价为 P 元，写出函数 P＝f(x)的表达式； y x= siny x= cosy x= x xy e e−= − tan 2α = tan 4 πα +   }{ na 11 =a 2 1 1 += −nn aa 2≥n }{ na 12 π 12 π 3 π 3 π ( ) ( )ln , 0,f x ax x x= ∈ +∞ ( )f x′ ( )f x ( )1 3f ′ = 32− 1 23 2log 5 (3)当销售商一次订购 500 个零件时，该厂获得的利润是多少？如果订购 1 000 个，利 润又是多少？(工厂售出一个零件的利润＝实际出厂单价－成本) 18. (本小题满分 12 分) 的内角 ， ， 所对的边分别为 ， ， ．向量 与 平行． （I）求 ； （II）若 ， 求 的面积． 19．(本小题满分 12 分)在平面直角坐标系 中，已知向量 ， ， 。 （1）若 ，求 tan x 的值 （2）若 与 的夹角为 ，求 的值。 20. (本小题满分 12 分)已知函数 ． (Ⅰ) 求 的最小正周期；(Ⅱ) 求 在区间 上的最小值． 21. (本小题满分 12 分)设函数 (1)求 在 处的切线方程。 （2）求 的单调区间和极值； 22. (本小题满分 14 分)等差数列 中， ， ． C∆ΑΒ Α Β C a b c ( ), 3m a b= ( )cos ,sinn = Α Β Α 7a = 2b = C∆ΑΒ xoy 2 2,2 2m  = −     ( )sin ,cosn x x= 0, 2x π ∈   m n⊥  m n 3 π x { }na 2 4a = 4 7 15a a+ = 2( ) 2 sin cos 2 sin2 2 2 x x xf x = − ( )f x ( )f x [ π 0]− ， ( ) 2 4ln2 xf x x= − ( )f x 1x = ( )f x （Ⅰ）求数列 的通项公式； （Ⅱ）设 ，求 的值． 长乐高级中学 2016-2017 学年第二学期期末考 高二数学（文科）试卷答案 一，选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1．命题“ ， ”的否定是（ C ） A． ， B． ， C． ， D． ， 2．已知集合 ， ，则 为( ) A． B． C． D． （2 答案 C）3．复数 等于( ) A． B． C． D． （3 答案 C） 4．条件 “ ”，条件 “ ”，则 是 的( ) A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 （4 答案 B） 5．函数 f(x)＝ 3x2 1－x＋lg(3x＋1)的定义域是(　　) A.(－ 1 3，＋∞)　　　　　　B.(－ 1 3，1) C.(－ 1 3， 1 3) D.(－∞，－ 1 3) 5．解析：由Error!⇒－ 1 3 x R∀ ∈ 2 2 1 0x x− + ≥ x R∀ ∈ 2 2 1 0x x− + < { }3,2,1=A { }2 2 0,B x x x x= − − = ∈R A B ∅ { }1 { }2 { }2,1 i1 i3 + + i21+ i21− i2 − i2 + :P 1x < :q ( )( )2 1 0x x+ − < P q 【解析】由已知得 ，又 ，所以 ，故 ． 7．已知两个单位向量 的夹角为 ,且满足 ,则实数 的值是( ) A． B． C． D． 7（答案 B） 8.在 中，已知 ， ， ，则 等于( ) A． B． C． D． 或 答案：D.解析：在 中，由 ，得 ，则 或 .故当 时， ；当 时， .故选 D. 9.要得到函数 的图象，只需将函数 的图像 (A)向左平移 个单位 (B) 向右平移 个单位 (C)向左平移 个单位 (D) 向右平移 个单位 9 解析： ，只需将函数 的图像向右平移 个单位答案选(B) 10.函数 y＝Asin(ωx＋φ)的部分图像如图 1­1 所示，则(　　) 图 1­1 A．y＝2sin（2x－ π 6 ） B．y＝2sin（2x－ π 3 ） C．y＝2sin（x＋ π 6 ） D．y＝2sin（x＋ π 3 ） 2( 2) 1 log 4 3f − = + = 2log 12 1> 2 2log 12 1 log 6 2(log 12) 2 2 6f −= = = 2( 2) (log 12) 9f f− + = 1 2,e e 45° ( )1 2 1 λ⊥ −e e e λ 1 2 2 3 3 2 ABC∆ 5 2a = 10c = o30A = B o105 o60 o15 o105 o15 ABC∆ sin sin a c A C = sin 2sin 2 c AC a = = o45C = o135C = o45C = o105B = o135C = o15B = sin(4 )3y x π= − sin 4y x= 12 π 12 π 3 π 3 π sin 4( )12y x π= − sin 4y x= 12 π 3．A　[解析] 由图知，A＝2，最小正周期 T＝π，所以 ω＝ 2π π ＝2，所以 y＝2sin(2x ＋φ)．又因为图像过点（ π 3 ，2），所以 2sin（2× π 3 ＋φ）＝2，即 2π 3 ＋φ＝2kπ＋ π 2 (k∈Z)，当 k＝0 时，得 φ＝－ π 6 ，所以 y＝2sin（2x－ π 6 ）. 11．某汽车运输公司购买了一批豪华大客车投入客运，据市场分析，每辆客车营运的总利润 y 万元与营运年数 x(x∈N)的关系为 y＝－x2＋12x－25，则每辆客车营运多少年报废可使其 营运年平均利润最大(　　) A．2　　　　 B．4　　　　 C．5　　　　　D．6 1．解析：设年平均利润为 g(x)，则 g(x)＝ －x2＋12x－25 x ＝12－(x＋ 25 x )． ∵x＋ 25 x ≥2 x· 25 x ＝10，∴当 x＝ 25 x ，即 x＝5 时， g(x)max＝2. 答案：C 12.下列函数为奇函数的是( ) A． B． C． D． 【11 答案】D 考点：函数的奇偶性． 第Ⅱ卷（非选择题 共 90 分） 二、填空题:本大题共 4 小题，每小题 4 分，共 16 分．把答案填在答题卡相应位置． 13.已知函数 ,其中 a 为实数, 为 的导函数,若 ,则 a 的值为 ． 【答案】3 【解析】 试题分析：因为 ,所以 . 14.(15 年北京文科) ， ， 三个数中最大数的是 ． 【答案】 试题分析： ， ， ，所以 最大. 15.已知 ． = 【答案】 ； y x= siny x= cosy x= x xy e e−= − tan 2α = tan 4 πα +   3− ( ) ( )ln , 0,f x ax x x= ∈ +∞ ( )f x′ ( )f x ( )1 3f ′ = ( ) ( )1 lnf x a x′ = + ( )1 3f a′ = = 32− 1 23 2log 5 2log 5 3 12 18 − = < 1 23 3 1= > 2 2log 5 log 4 2 3> > > 2log 5 16.已知数列 中， ， （ ），则数列 的前 9 项和等于 。 【答案】27 考点：1.等差数列的定义；2.等差数列的前 n 项和. 三、解答题：本大题共 6 小题，共 74 分．解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分 12 分)某工厂生产某种零件，每个零件的成本为 40 元，出厂单价定为 60 元，该厂为鼓励销售商订购，决定当一次订购量超过 100 个时，每多订购一个，订购的 全部零件的出厂单价就降低 0.02 元，但实际出厂单价不能低于 51 元． (1)当一次订购量为多少时，零件的实际出厂单价恰为 51 元； (2)设一次订购量为 x 个，零件的实际出厂单价为 P 元，写出函数 P＝f(x)的表达式； (3)当销售商一次订购 500 个零件时，该厂获得的利润是多少？如果订购 1 000 个，利 润又是多少？(工厂售出一个零件的利润＝实际出厂单价－成本) 17．【解析】　(1)设订购 x 个，单价为 51 元． 60－(x－100)×0.02＝51， ∴x＝550. (2)当 0＜x≤100 且 x∈Z 时，P＝60； 当 100＜x≤550 且 x∈Z 时， P＝60－(x－100)×0.02 ＝62－0.02x； 当 x＞550 且 x∈Z 时，P＝51. ∴P＝ Error! (3)订购 500 个零件， 利润为 500×[(62－0.02×500)－40]＝6 000(元)； 订购 1 000 个零件，利润为 1 000×(51－40)＝11 000(元)． 18. (本小题满分 12 分) 的内角 ， ， 所对的边分别为 ， ， ．向量 与 平行． （I）求 ； （II）若 ， 求 的面积． 【答案】（I） ；（II） ． }{ na 11 =a 2 1 1 += −nn aa 2≥n }{ na C∆ΑΒ Α Β C a b c ( ), 3m a b= ( )cos ,sinn = Α Β Α 7a = 2b = C∆ΑΒ 3 π 3 3 2 试题解析：（I）因为 ，所以 ， 由正弦定理，得 又 ，从而 ， 由于 ，所以 (II)解法一：由余弦定理，得 而 得 ，即 因为 ，所以 . 故 ABC 的面积为 . 考点：1、平行向量的坐标运算；2、正弦定理；3、余弦定理；4、三角形的面积公式. 19．(本小题满分 12 分)在平面直角坐标系 中，已知向量 ， //m n  sin 3 cos 0a B b A- = sinAsinB 3sinBcosA 0- = sin 0Β ≠ tan 3A = 0 A π< < 3A π= 2 2 2 2 cosa b c bc A= + - 7 b 2,a = = 3 πΑ = 27 4 2c c= + - 2 2 3 0c c- - = 0c > 3c = ∆ 1 3 3bcsinA2 2= xoy 2 2,2 2m  = −     ， 。 （1）若 ，求 tan x 的值 （2）若 与 的夹角为 ，求 的值。 【答案】（1） ；（2） ． 【考点定位】本题考查向量数量积的坐标运算、两角和差公式的逆用、知角求值、值知求角 等问题，属于中档题． 20. (本小题满分 12 分)已知函数 ． (Ⅰ) 求 的最小正周期； (Ⅱ) 求 在区间 上的最小值． 【答案】（1） ，（2） 【解析】 ( )sin ,cosn x x= 0, 2x π ∈   m n⊥  m n 3 π x 1 5 12x π= 2( ) 2 sin cos 2 sin2 2 2 x x xf x = − ( )f x ( )f x [ π 0]− ， 2π 21 2 − − 试题分析：先用降幂公式和辅助角公式进行三角恒等变形，把函数化为 形式，再利用周期公式 求出周期，第二步由 于 则可求出 ，借助正弦函数图象 找出在这个范 围内当 ，即 时， 取得最小值为： . 试题解析：(Ⅰ) (1) 的最小正周期为 ； (2) ，当 时， 取得最小值为： 21. (本小题满分 12 分)设函数 (1)求 在 处的切线方程。 （2）求 的单调区间和极值； 【答案】（1） 切线方程为 即 （2）单调递减区间是 ，单调递增区间是 ；极小值 ；（2） 证明详见解析. ( ) si n( )f x A x mω ϕ= + + 2T π ω= 0,xπ− ≤ ≤ 3 4 4 4x π π π− ≤ + ≤ 4 2x π π+ = − 3 4x π= − ( )f x 21 2 − − 2 1 1 cos( ) 2 si n cos 2 si n 2 si n 22 2 2 2 2 x x x xf x x −= − = ⋅ − ⋅ = 2 2 2si n cos2 2 2x x= + − 2si n( )4 2x π= + − ( )f x 2 21T π π= = 30, 4 4 4x x π π ππ− ≤ ≤ ∴ − ≤ + ≤ 3,4 2 4x x π π π+ = − = − ( )f x 21 2 − − ( ) 2 4ln2 xf x x= − ( )f x 1x = ( )f x ( ) 11 2f = ( ) 4f x x x ′ = − ( )1 1 4 3f ′ = − = − 1 3( 1)2y x− = − − 73 02x y+ − = (0,2) (2, )+∞ 4(1 ln 4)(2) 2f −= 所以， 的单调递减区间是 ，单调递增区间是 ； 在 处取得极小值 . 22. (本小题满分 42 分)等差数列 中， ， ． （Ⅰ）求数列 的通项公式； （Ⅱ）设 ，求 的值． 【答案】（Ⅰ） ；（Ⅱ） ． 【解析】 试题分析：（Ⅰ）利用基本量法可求得 ，进而求 的通项公式；（Ⅱ）求数列前 n { }na 2 4a = 4 7 15a a+ = { }na 22 na nb n−= + 1 2 3 10b b b b+ + +⋅⋅⋅+ 2na n= + 2101 1,a d { }na ( )f x (0, )k ( , )k +∞ ( )f x x k= (1 ln )( ) 2 k kf k −= 项和，首先考虑其通项公式，根据通项公式的不同特点，选择相应的求和方法，本题 ，故可采取分组求和法求其前 10 项和． 试题解析：（I）设等差数列 的公差为 ． 由已知得 ， 解得 ． 所以 ． 考点：1、等差数列通项公式；2、分组求和法． 2n nb n= + { }na d ( ) ( ) 1 1 1 4 3 6 15 a d a d a d + = + + + = 1 3 1 a d =  = ( )1 1 2na a n d n= + − = +