- 2021-06-23 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2019届辽宁省大连市普兰店市第六中学高二上学期期中考试(2017-11)
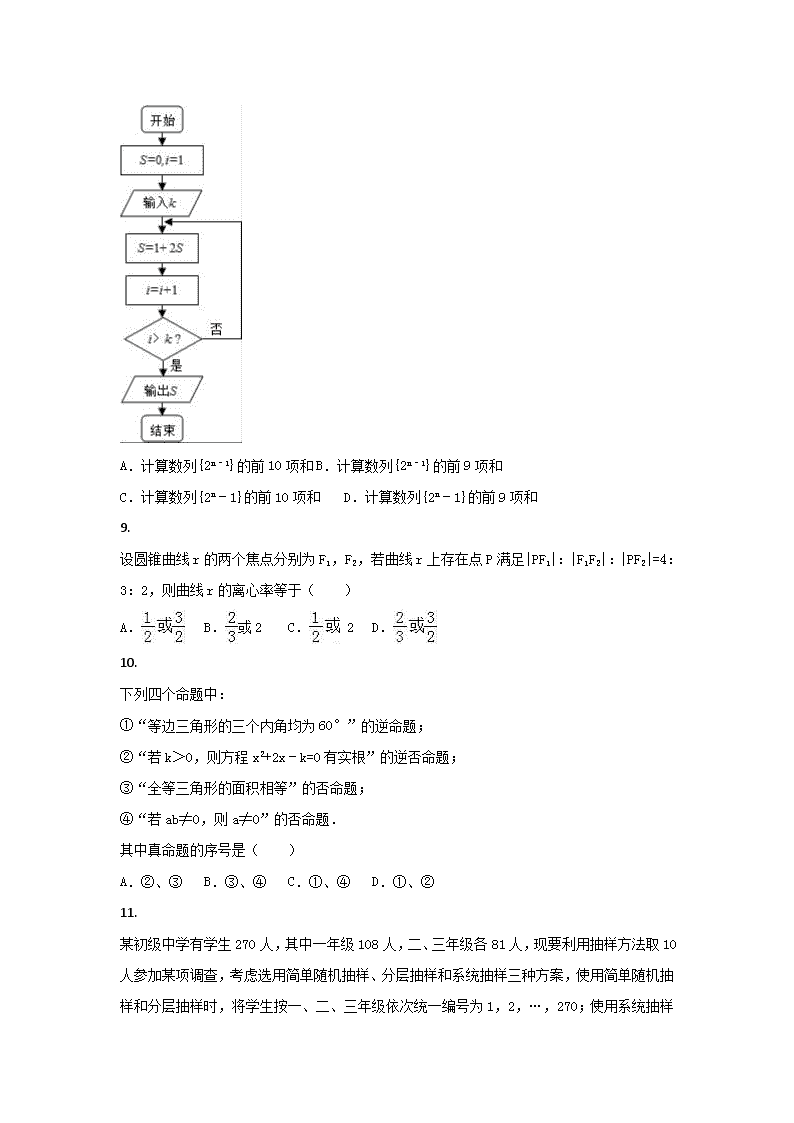
高二上学期期中数学(理)试题 题号 一 二 三 总分 得分 评卷人 得分 一、选择题 本大题共12道小题。 1. 如表是某厂1﹣4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程是=﹣0.7x+,则=( ) 月份x 1 2 3 4 用水量y 4.5 4 3 2.5 A.10.5 B.5.15 C.5.25 D.5.2 2. 抛物线x2=﹣8y的焦点坐标是( ) A.(0,2) B.(0,﹣2) C.(0,4) D.(0,﹣4) 3. 已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数: 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,该运动员三次投篮恰有两次命中的概率为( ) A.0.35 B.0.25 C.0.20 D.0.15 4. 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50), [50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) A.588 B.480 C.450 D.120 5. 已知P:x2﹣x<0,那么命题P的一个必要非充分条件是( ) A.0<x<1 B.﹣1<x<1 C.<x< D.<x<2 6. 已知命题p:∀x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)≥0,则¬p是( ) A.∃x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)≤0 B.∀x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)≤0 C.∃x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)<0 D.∀x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)<0 7. 若方程+=1表示双曲线,则k的取值范围是( ) A.(5,10) B.(﹣∞,5) C.(10,+∞) D.(﹣∞,5)∪(10,+∞) 8. 阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( ) A.计算数列{2n﹣1}的前10项和 B.计算数列{2n﹣1}的前9项和 C.计算数列{2n﹣1}的前10项和 D.计算数列{2n﹣1}的前9项和 9. 设圆锥曲线r的两个焦点分别为F1,F2,若曲线r上存在点P满足|PF1|:|F1F2|:|PF2|=4:3:2,则曲线r的离心率等于( ) A. B.或2 C. 2 D. 10. 下列四个命题中: ①“等边三角形的三个内角均为60°”的逆命题; ②“若k>0,则方程x2+2x﹣k=0有实根”的逆否命题; ③“全等三角形的面积相等”的否命题; ④“若ab≠0,则a≠0”的否命题. 其中真命题的序号是( ) A.②、③ B.③、④ C.①、④ D.①、② 11. 某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况: ①7,34,61,88,115,142,169,196,223,250; ②5,9,100,107,111,121,180,195,200,265; ③11,38,65,92,119,146,173,200,227,254; ④30,57,84,111,138,165,192,219,246,270; 关于上述样本的下列结论中,正确的是( ) A.②、③都不能为系统抽样 B.②、④都不能为分层抽样 C.①、④都可能为系统抽样 D.①、③都可能为分层抽样 12. 下图是2008年我校举办“激扬青春,勇担责任”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为( ) A.85;87 B.84;86 C.84;85 D.85;86 评卷人 得分 一、填空题 本大题共4道小题。 13. 椭圆E: +=1内有一点P(2,1),则经过P并且以P为中点的弦所在直线方程为 . 14. 如图给出的是计算++++…+ 的值的一个程序框图,其中判断框内应填入的条件是 ? 15. 一支田径队有男女运动员98人,其中男运动员有56人.按男女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是 . 16. 在等腰Rt△ABC中,在斜边AB上任取一点M,则AM的长小于AC的长的概率为 . 评卷人 得分 二、解答题 本大题共6道小题。 17. 给出命题p:a(1﹣a)>0;命题q:y=x2+(2a﹣3)x+1与x轴交于不同的两点.如果命题“p∨q”为真,“p∧q”为假,求a的取值范围. 18. 已知双曲线的一条渐近线为y﹣x=0,且过点(,1) (1)求双曲线的标准方程; (2)若直线y=kx﹣1与上述所得双曲线只有一个公共点,求k的值. 19. 袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球 (Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果; (Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率. 20. 如图,椭圆E:的左焦点为F1,右焦点为F2,离心率e=.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8. (Ⅰ)求椭圆E的方程. (Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由. 21. 如图,某校100名学生期中考试语文成绩的频率分布直方图,其中成绩分组区间是:(50,60),(60,70),(70,80),(80,90),(90,100). (1)图中语文成绩的众数是 . (2)求图中a的值; (3)根据频率分布直方图,估计这100名学生语文成绩的平均分和中位数(中位数要求精确到小数点后一位). 22. 如图,已知直线l:y=2x﹣4交抛物线y2=4x于A、B两点,试在抛物线AOB这段曲线上求一点P,使△ABP的面积最大,并求这个最大面积. 试卷答案 1.C 【考点】线性回归方程. 【分析】计算样本中心,代入回归方程得出. 【解答】解: =, =3.5. ∴3.5=﹣0.7×2.5+,解得=5.25. 故选C. 【点评】本题考查了线性回归方程经过样本中心的性质,属于基础题. 2.B 【考点】抛物线的简单性质. 【分析】由x2=﹣2py(p>0)的焦点为(0,﹣),则抛物线x2=﹣8y的焦点坐标即可得到. 【解答】解:由x2=﹣2py(p>0)的焦点为(0,﹣), 则抛物线x2=﹣8y的焦点坐标是(0,﹣2). 故选B. 【点评】本题考查抛物线的方程和性质,主要考查抛物线的焦点坐标,属于基础题. 3.A 【考点】模拟方法估计概率. 【分析】由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,在20组随机数中表示三次投篮恰有两次命中的有可以通过列举得到共5组随机数,根据概率公式,得到结果. 【解答】解:由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数, 在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、431、393、113. 共7组随机数, ∴所求概率为=0.35. 故选A. 【点评】本题考查模拟方法估计概率,是一个基础题,解这种题目的主要依据是等可能事件的概率,注意列举法在本题的应用. 4.B 【考点】频率分布直方图. 【分析】根据频率分布直方图,成绩不低于60分的频率,然后根据频数=频率×总数可求出所求. 【解答】解:根据频率分布直方图,成绩不低于60(分)的频率为 1﹣10×(0.005+0.015)=0.8, 可估计该该模块测试成绩不少于60分的学生人数为 600×0.8=480(人). 故选:B. 【点评】本题主要考查了频率、频数、统计和概率等知识,属于基础题. 5.B 【考点】必要条件、充分条件与充要条件的判断. 【分析】求出不等式的等价条件,结合必要不充分条件的定义进行判断即可. 【解答】解:由x2﹣x<0得0<x<1,设A=(0,1), 设0<x<1成立的一个必要不充分条件为B, 则满足A⊊B, 显然﹣1<x<1满足条件., 故选:B. 【点评】本题主要考查充分条件和必要条件的应用,比较基础. 6.C 【考点】命题的否定. 【分析】由题意,命题p是一个全称命题,把条件中的全称量词改为存在量词,结论的否定作结论即可得到它的否定,由此规则写出其否定,对照选项即可得出正确选项 【解答】解:命题p:∀x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)≥0是一个全称命题,其否定是一个特称命题, 故¬p:∃x1,x2∈R,(f(x2)﹣f(x1))(x2﹣x1)<0. 故选:C. 【点评】本题考查命题否定,解题的关键是熟练掌握全称命题的否定的书写规则,本题易因为没有将全称量词改为存在量词而导致错误,学习时要注意准确把握规律. 7.A 【考点】双曲线的简单性质. 【分析】根据题意,由双曲线的标准方程的形式分析可得(10﹣k)与(5﹣k)异号,即可得(10﹣k)(5﹣k)<0,解可得k的范围,即可得答案. 【解答】解:根据题意,方程+=1表示双曲线, 必有(10﹣k)与(5﹣k)异号, 即有(10﹣k)(5﹣k)<0, 解可得5<k<10, 即k的取值范围是(5,10); 故选:A. 【点评】本题考查双曲线的标准方程,关键是注意双曲线标准方程的形式,即二元二次方程在什么条件下表示双曲线. 8.A 【考点】程序框图. 【分析】从赋值框给出的两个变量的值开始,逐渐分析写出程序运行的每一步,便可得到程序框图表示的算法的功能. 【解答】解:框图首先给累加变量S和循环变量i赋值, S=0,i=1; 判断i>10不成立,执行S=1+2×0=1,i=1+1=2; 判断i>10不成立,执行S=1+2×1=1+2,i=2+1=3; 判断i>10不成立,执行S=1+2×(1+2)=1+2+22,i=3+1=4; … 判断i>10不成立,执行S=1+2+22+…+29,i=10+1=11; 判断i>10成立,输出S=1+2+22+…+29. 算法结束. 故则该算法的功能是计算数列{2n﹣1}的前10项和. 故选A. 【点评】本题考查解决程序框图中的循环结构时,常采用写出前几次循环的结果,找规律. 9.A 【考点】圆锥曲线的共同特征. 【分析】根据题意可设出|PF1|,|F1F2|和|PF2|,然后分曲线为椭圆和双曲线两种情况,分别利用定义表示出a和c,则离心率可得. 【解答】解:依题意设|PF1|=4t,|F1F2|=3t,|PF2|=2t, 若曲线为椭圆则2a=|PF1|+|PF2|=6t,c=t 则e==, 若曲线为双曲线则,2a=4t﹣2t=2t,a=t,c=t ∴e== 故选A 【点评】本题主要考查了圆锥曲线的共同特征.关键是利用圆锥曲线的定义来解决. 10.D 【考点】命题的真假判断与应用. 【分析】①,逆命题:三个内角均为60°的三角形是等边三角形; ②,原命题为真,其逆否命题与原命题同真假; ③,“全等三角形的面积相等”的否命题:不全等三角形的不面积相等; ④,“若ab=0,则a=0或b=0”. 【解答】解:对于①“等边三角形的三个内角均为60°”的逆命题:三个内角均为60°的三角形是等边三角形,故为真命题; 对于②,“若k>0,则方程x2+2x﹣k=0的△=4+4k>0,有实根”,∴原命题为真,其逆否命题与原命题同真假,故为真命题; 对于③,“全等三角形的面积相等”的否命题:不全等三角形的不面积相等,故为假命题; 对于④,“若ab≠0,则a≠0”的否命题:“若ab=0,则a=0”,故为假命题. 故选:D 【点评】本题考查了命题的四种形式的转换,及真假判定,属于基础题. 11.D 【考点】收集数据的方法. 【分析】观察所给的四组数据,根据四组数据的特点,把所用的抽样选出来,①,③可能是系统抽样或分层抽样,②是简单随机抽样,④一定不是系统抽样和分层抽样. 【解答】解:观察所给的四组数据, ①,③可能是系统抽样或分层抽样, ②是简单随机抽样, ④一定不是系统抽样和分层抽样, 故选D. 【点评】简单随机抽样是一种最简单、最基本的抽样方法.常用的简单随机抽样方法有抽签法和随机数法.简单随机抽样和系统抽样过程中,每个个体被抽取的可能性是相等的. 12.C 【考点】茎叶图;众数、中位数、平均数. 【分析】本茎叶图表示的数据是两位数,读出数据后,根据题意,去掉两个数据79,93后,研究剩下5个数据的中位数、平均数. 【解答】解:由题意知去掉一个最高分93和一个最低分79后, 所剩数据的数据是84,84,84,86,87 中间一位是84,所以中位数是84. 这组数据的平均数是 (84+84+84+86+87)÷5=85 故选C 【点评】本题考查样本的平均数、方差,属基础题,熟记样本的平均数、方差公式是前提,准确计算是关键 13.x+2y﹣4=0 【考点】直线与圆锥曲线的关系. 【分析】设所求直线与椭圆相交的两点的坐标,然后利用点差法求得直线的斜率,最后代入直线方程的点斜式得答案. 【解答】解:设所求直线与椭圆相交于A(x1,y1),B(x2,y2), 则,. 两式相减得. 又x1+x2=4,y1+y2=2, ∴kAB=. 因此所求直线方程为y﹣1=﹣(x﹣2),即x+2y﹣4=0. 故答案为:x+2y﹣4=0. 【点评】本题考查了直线与圆锥曲线的关系,训练了点差法求与中点弦有关的问题,是中档题. 14.i<51或(i<=50) 【考点】程序框图. 【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值,模拟循环过程可得条件. 【解答】解:程序运行过程中,各变量值如下表所示: 第一圈:S=0+,i=2, 第二圈:S=+,i=3, 第三圈:S=++,i=4, … 依此类推, 第49圈:S=++++…+,i=50, 第50圈:S=++++…+,i=51, 退出循环 其中判断框内应填入的条件是:i<51或(i<=50), 故答案为:i<51或(i<=50) 【点评】算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误. 15.12 【考点】分层抽样方法. 【分析】根据田径队的男女运动员数目和用分层抽样要抽取的数目,得到每个个体被抽到的概率,利用每个个体被抽到的概率乘以女运动员的数目,得到结果. 【解答】解:∵田径队有男女运动员98人,其中男运动员有56人, ∴这支田径队有女运动员98﹣56=42人, 用分层抽样的方法从该队的全体运动员中抽取一个容量为28的样本, ∴每个个体被抽到的概率是= ∵田径队有女运动员42人, ∴女运动员要抽取42×=12人, 故答案为:12 【点评】本题主要考查了分层抽样,在抽样过程中每个个体被抽到的概率相等,这是解决这种问题的依据,属于基础题. 16. 【考点】几何概型. 【分析】欲求AM的长小于AC的长的概率,先求出M点可能在的位置的长度,AC的长度,再让两者相除即可. 【解答】解:在AB上截取AC′=AC, 于是P(AM<AC)=P(AM<AC′)==. 答:AM的长小于AC的长的概率为. 故答案为:. 【点评】本题主要考查了概率里的古典概型.在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,其中对于几何度量为长度,面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的. 17. 【考点】复合命题的真假. 【分析】先求出命题p,q为真命题时对应的等价条件,然后利用p∧q为假命题,p∨q为真命题,确定a的取值范围. 【解答】解:命题p为真⇔a(1﹣a)>0⇔0<a<1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分) 命题q为真,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣ 命题“p∨q”为真,“p∧q”为假⇔p,q中一真一假,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分) 当p真q假时,,得,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分) 当p假q真时,,得,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分) 所以a的取值范围是﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分) 【点评】本题考查了复合命题的真假判断以及应用,要求熟练掌握复合命题与简单命题的真假关系,属于基础题. 18. 【考点】双曲线的简单性质. 【分析】(1)设出方程,代入点,即可求双曲线的标准方程; (2)由得(1﹣k2)x2+2kx﹣5=0.①因为直线与双曲线只有一个公共点,则①式方程只有一解,分类讨论,求k的值. 【解答】解:(1)依题意设双曲线方程为x2﹣y2=λ 又因为点(,1)在双曲线上,可得λ=4, 所求的双曲线方程为x2﹣y2=4﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣ (2)由得(1﹣k2)x2+2kx﹣5=0.① 因为直线与双曲线只有一个公共点,则①式方程只有一解. 当1﹣k2=0,即k=±1时,①式方程只有一解; 当1﹣k2≠0时,应满足△=4k2+20(1﹣k2)=0, 解得k=±,故k的值为±1或±.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分) 【点评】本题考查双曲线的方程,考查直线与双曲线的位置关系,属于中档题. 19. 【考点】等可能事件的概率;随机事件. 【分析】(1)由分步计数原理知这个过程一共有8个结果,按照一定的顺序列举出所有的事件,顺序可以是按照红球的个数由多变少变化,这样可以做到不重不漏. (2)本题是一个等可能事件的概率,由前面可知试验发生的所有事件数,而满足条件的事件包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红),根据古典概型公式得到结果. 【解答】解:(I)一共有8种不同的结果,列举如下: (红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑) (Ⅱ)本题是一个等可能事件的概率 记“3次摸球所得总分为5”为事件A 事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3 由(I)可知,基本事件总数为8, ∴事件A的概率为 【点评】用列举法列举基本事件的个数,不仅能让学生直观的感受到对象的总数,而且还能使学生在列举的时候注意作到不重不漏.解决了求古典概型中基本事件总数这一难点. 20. 【考点】直线与圆锥曲线的综合问题;椭圆的标准方程. 【分析】(Ⅰ)根据过F1的直线交椭圆于A、B两点,且△ABF2的周长为8,可得4a=8,即a=2,利用e=,b2=a2﹣c2=3,即可求得椭圆E的方程. (Ⅱ)由,消元可得(4k2+3)x2+8kmx+4m2﹣12=0,利用动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0),可得m≠0,△=0,进而可得P(,),由得Q(4,4k+m),取k=0,m=;k=,m=2,猜想满足条件的点M存在,只能是M(1,0),再进行证明即可. 【解答】解:(Ⅰ)∵过F1的直线交椭圆于A、B两点,且△ABF2的周长为8. ∴4a=8,∴a=2 ∵e=,∴c=1 ∴b2=a2﹣c2=3 ∴椭圆E的方程为. (Ⅱ)由,消元可得(4k2+3)x2+8kmx+4m2﹣12=0 ∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0) ∴m≠0,△=0,∴(8km)2﹣4×(4k2+3)×(4m2﹣12)=0 ∴4k2﹣m2+3=0① 此时x0==,y0=,即P(,) 由得Q(4,4k+m) 取k=0,m=,此时P(0,),Q(4,),以PQ为直径的圆为(x﹣2)2+(y﹣)2=4,交x轴于点M1(1,0)或M2(3,0) 取k=,m=2,此时P(1,),Q(4,0),以PQ为直径的圆为(x﹣)2+(y﹣)2=,交x轴于点M3(1,0)或M4(4,0) 故若满足条件的点M存在,只能是M(1,0),证明如下 ∵ ∴ 故以PQ为直径的圆恒过x轴上的定点M(1,0) 方法二: 假设平面内存在定点M满足条件,因为对于任意以PQ为直径的圆恒过定点M,所以当PQ平行于x轴时,圆也过定点M,即此时P点坐标为(0,)或(0,﹣),由图形对称性知两个圆在x轴上过相同的交点,即点M必在x轴上.设M(x1,0),则•=0对满足①式的m,k恒成立. 因为=(﹣﹣x1,), =(4﹣x1,4k+m),由•=0得﹣+﹣4x1+x12++3=0 21.(1)65(2) 0.005.(3)71.7分. 【考点】频率分布直方图;众数、中位数、平均数. 【分析】(1)利用众数的意义即可得出; (2)根据频率分布直方图中各小矩形面积之和等于1即可得出; (3)根据平均数和中位数的意义即可得出. 【解答】解:(1)众数是65. (2)依题意得,10(2a+0.02+0.03+0.04)=1,解得a=0.005. (3)这100名学生语文成绩的平均分为:55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分). 设中位数为70+x分,则由0.005×10+0.04×10+0.03x=0.5 解得, ∴这100名学生语文成绩的中位数约为71.7分. 【点评】熟练掌握利用频率分布直方图求众数、平均数、中位数及知道频率分布直方图中各小矩形面积之和等于1等性质是解题的关键. 22. 【考点】直线与圆锥曲线的综合问题. 【分析】直线l:y=2x﹣4与抛物线y2=4x联立,求出A,B的坐标,可得|AB|,求出P到直线l的距离的最大值,即可得出P的坐标,及最大面积. 【解答】解:由得:4x2﹣20x+16=0,即x2﹣5x+4=0, 所以A(4,4)、B(1,﹣2). 故.… 设点P(t2,2t)(﹣1<t<2),则P到直线l的距离为:, 所以. 故当,即点时,△ABP的面积最大为.…(12分) 【点评】本题考查直线与抛物线的位置关系,考查点到直线距离公式的运用,正确求出P到直线l的距离是关键.查看更多