数学卷·2019届黑龙江省大庆一中高二上学期第二次月考（2017-10）

数学卷·2019届黑龙江省大庆一中高二上学期第二次月考（2017-10）

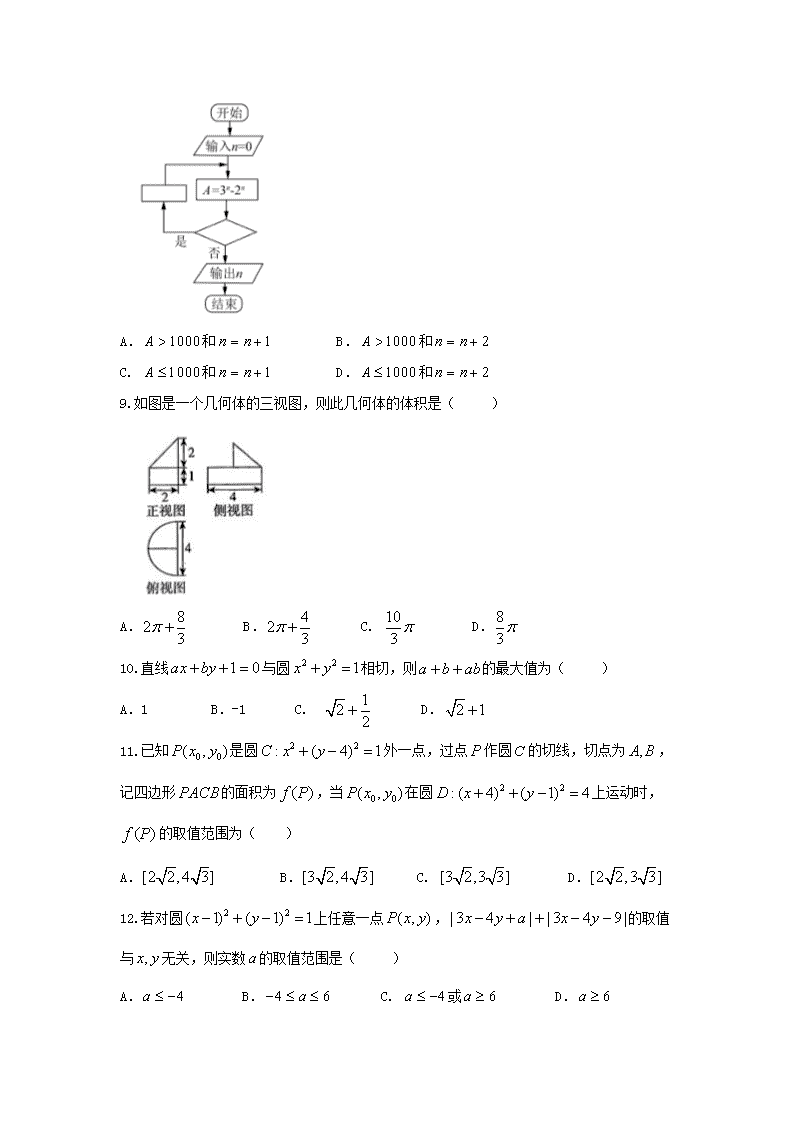
大庆一中高二年级上学期第二月考 数学试卷 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知是直线的倾斜角，则的值是（ ）‎ A． B． C． D．‎ ‎2.用“辗转相除法”求得459和357的最大公约数是（ ）‎ A． 3 B． 9 C． 17 D．51‎ ‎3.若直线与直线平行，则（ ）‎ A．2或-1 B． 2 C． -1 D． 以上都不对 ‎4.某校为了解1000名高一新生的身体生长状况，用系统抽样法（按等距的规则）抽取40名同学进行检查，将学生从11000进行编号，现已知第18组抽取的号码为443，则第一组用简单随机抽样抽取的号码为（ ）‎ A． 16 B．17 C. 18 D．19‎ ‎5.在中，角所对的边分别为，且满足，则一定是（ ）‎ A．等腰三角形 B．直角三角形 C.等边三角形 D．等腰直角三角形 ‎6.已知正四面体中，是的中点，则异面直线与所成角的余弦值为（ ）‎ A． B． C. D．‎ ‎7.若曲线与直线有公共点，则的取值范围是（ ）‎ A． B． C. D．‎ ‎8.如下程序框图是为了求出满足的最小偶数，那么在和两个空白框中，可以分别填入（ ）‎ A．和 B．和 ‎ C. 和 D．和 ‎ ‎9.如图是一个几何体的三视图，则此几何体的体积是（ ）‎ A． B． C. D．‎ ‎10.直线与圆相切，则的最大值为（ ）‎ A．1 B．-1 C. D．‎ ‎11.已知是圆外一点，过点作圆的切线，切点为，记四边形的面积为，当在圆上运动时，的取值范围为（ ）‎ A． B． C. D．‎ ‎12.若对圆上任意一点，的取值与无关，则实数的取值范围是（ ）‎ A． B． C. 或 D．‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.把“五进制”数转化为“十进制”数，再把它转化为“八进制”数： ． ‎ ‎14.过点向圆所引的切线方程为 ．‎ ‎15.已知圆：及一点，在圆上运动一周，的中点形成轨迹的方程为 ．‎ ‎16.在矩形中，，，动点在以点为圆心且与相切的圆上，若，则的最大值为 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 已知圆过两点，，且圆心在直线上.‎ ‎（1）求圆的标准方程；‎ ‎（2）直线过点且与圆有两个不同的交点，若直线的斜率大于0，求的取值范围.‎ ‎18. 在中，角所对的边分别为，已知.‎ ‎（1）求角；‎ ‎（2）若，的面积为，求.‎ ‎19. 某班100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是，，，，.‎ ‎（1）求图中的值；‎ ‎（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎（3）若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数之比如表所示，求数学成绩在之外的人数.‎ ‎20. 等差数列的前项和为，且，.‎ ‎（1）求数列的通项公式；‎ ‎（2）若数列满足且，求数列的前项和.‎ ‎21. 如图所示，在四棱锥中，底面是边长为2的正方形，侧面为正三角形，且面面，分别为棱的中点.‎ ‎（1）求证：平面；‎ ‎（2）（文科）求三棱锥的体积；‎ ‎（理科）求二面角的正切值.‎ ‎22.已知动直线过点，且与圆：交于两点.‎ ‎（1）若直线的斜率为，求的面积；‎ ‎（2）若直线的斜率为0，点是圆上任意一点，求的取值范围；‎ ‎（3）是否存在一个定点（不同于点），对于任意不与轴重合的直线，都有平分 ‎，若存在，求出定点的坐标；若不存在，请说明理由.‎ 试卷答案 一、选择题 ‎1-5:BDCCA 6-10:BCDDC 11、12：AD 二、填空题 ‎13. 302 14. 15. 16.3‎ 三、解答题 ‎17. （I）MN的垂直平分线方程为：x﹣2y﹣1=0与2x﹣y﹣2=0联立解得圆心坐标为C（1，0）‎ R2=|CM|2=（﹣3﹣1）2+（3﹣0）2=25‎ ‎∴圆C的标准方程为：（x﹣1）2+y2=25 ‎ ‎（II）设直线的方程为：y﹣5=k（x+2）即kx﹣y+2k+5=0，设C到直线l的距离为d，‎ 则d=‎ 由题意：d＜5‎ 即：8k2﹣15k＞0‎ ‎∴k＜0或k＞‎ 又因为k＞0‎ ‎∴k的取值范围是（，+∞） ‎ ‎18. （Ⅰ）由已知及正弦定理得：，‎ 即，‎ 因为，所以，‎ 因为，所以. ‎ ‎（另解：因为，‎ 所以，‎ 因为，所以.）‎ ‎（Ⅱ）因为的面积为，所以，‎ 由余弦定理得：，‎ 即，‎ 所以. ‎ ‎19. （Ⅰ）由频率分布直方图，可得，‎ 因此 ‎（Ⅱ）73,‎ 所以这100名学生的语文成绩的平均分为73分.‎ ‎ (Ⅲ)分别求出语文成绩在分数段，，，的人数依次为 所以数学成绩分数段在，，，的人数依次为5,20,40,25.‎ 所以数学成绩在之外的人数有人.‎ ‎20. （Ⅰ）设等差数列的公差为，‎ ‎∵∴，‎ 解得．∴‎ ‎（Ⅱ）∵，，‎ 当时，‎ 当时，适合上式，所以 ‎．‎ ‎. ‎ ‎21.‎ ‎（1）证明：取PD中点G，连结GF、AG，‎ ‎∵GF为△PDC的中位线，∴GF∥CD且，‎ 又AE∥CD且，∴GF∥AE且GF=AE，‎ ‎∴EFGA是平行四边形，则EF∥AG，‎ 又EF⊥面PAD，AG⊥面PAD，‎ ‎∴EF∥面PAD； ‎ ‎（2）（文）解：取AD中点O，连结PO，‎ ‎∵面PAD⊥面ABCD，△PAD为正三角形，∴PO⊥面ABCD，且，‎ 又PC为面ABCD斜线，F为PC中点，∴F到面ABCD距离，‎ 故；‎ ‎（理）解：连OB交CE于M，可得Rt△EBC≌Rt△OAB，‎ ‎∴∠MEB=∠AOB，则∠MEB+∠MBE=90°，即OM⊥EC．‎ 连PM，又由（2）知PO⊥EC，可得EC⊥平面POM，则PM⊥EC，‎ 即∠PMO是二面角P-EC-D的平面角，‎ 在Rt△EBC中，，∴，‎ ‎∴，即二面角P-EC-D的正切值为． ‎ （1） ‎22.(1) 因为直线，则点到直线的距离 弦的长度，则.‎ ‎（2）因为直线的斜率为，所以可知、，‎ 设点，则，又，‎ 则，又，的取值范围是.‎ ‎（3）若存在，则根据对称性可知，定点在轴上，设、又设、，因直线不与轴重合，设直线，代入圆得，所以 ‎（1）‎ 若平分，则根据角平分线的定义，与的斜率互为相反数 有，又，，‎ 化简可得，代入（1）式得，因为直线任意，故，即，即 ‎