2013年全国高校自主招生数学模拟试卷7

2013年全国高校自主招生数学模拟试卷7

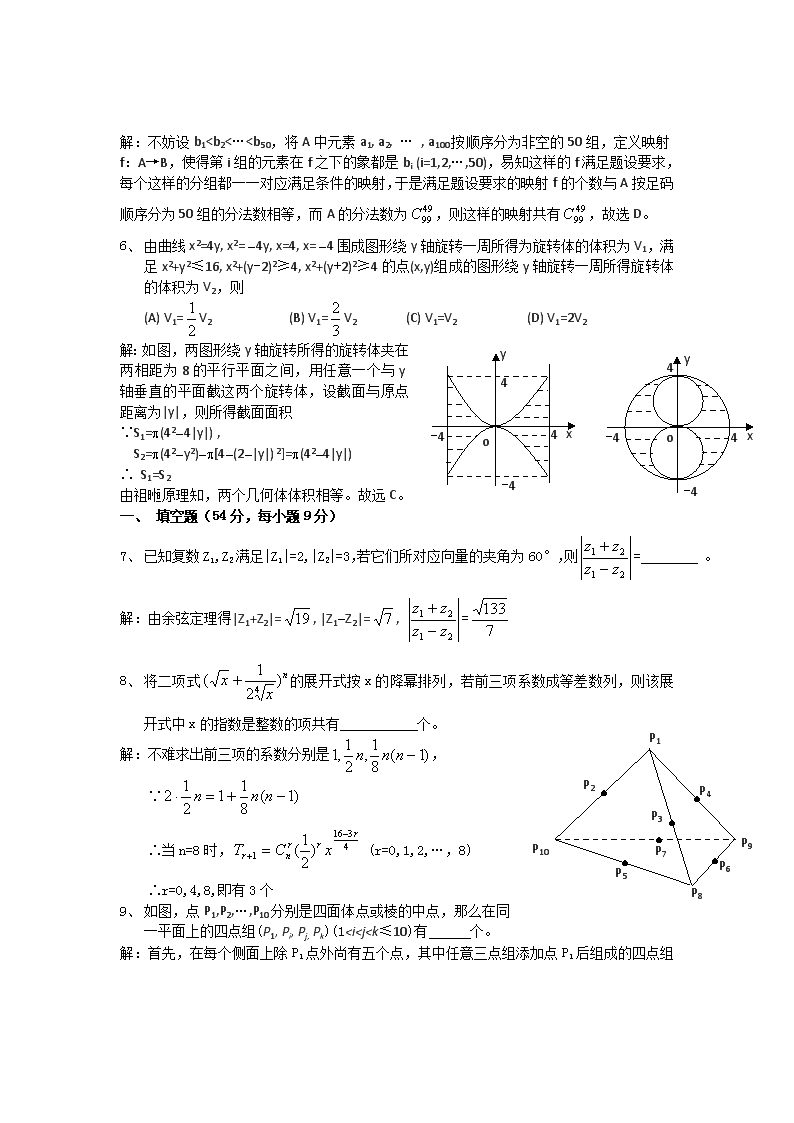
‎2013年全国高校自主招生数学模拟试卷七 一．选择题（36分，每小题6分）‎ 1、 函数f(x)=的单调递增区间是 ‎(A) (-∞，-1) (B) (-∞，1) (C) (1，+∞) (D) (3，+∞)‎ 解：由x2-2x-3>0x<-1或x>3，令f(x)=, u= x2-2x-3，故选A 2、 若实数x, y满足(x+5)2+(y-12)2=142，则x2+y2的最小值为 ‎ (A) 2 (B) 1 (C) (D) ‎ 解：B 3、 函数f(x)=‎ ‎(A) 是偶函数但不是奇函数 (B) 是奇函数但不是偶函数 ‎(C) 既是奇函数又是偶函数 (D) 既不是奇函数又不是偶函数 解：A 4、 直线椭圆相交于A，B两点，该圆上点P，使得⊿PAB面积等于3，这样的点P共有 ‎(A) 1个 (B) 2个 (C) 3个 (D) 4个 解：设P1(4cosa,3sina) (00，所以只须求x-y的最小值。‎ ‎　　令x-y=u代入x2-4y2=4中有3y2-2uy+(4-u2)=0‎ ‎ ∵y∈R ‎ ∴⊿≥0‎ ‎ ∴当时，u=，故|x|-|y|的最小值是 3、 使不等式sin2x+acosx+a2≥1+cosx对一切x∈R恒成立的负数a的取值范围是 。‎ 解：∵sin2x+acosx+a2≥1+cosx ‎　　∴‎ ‎　　∵a<0,‎ ‎∴当cosx=1时，函数有最大值 ‎∴a2+a-2≥‎0a≤-2或a≥1‎ ‎∵a<0‎ ‎∴负数a的取值范围是(-∞,2]‎ 一、 解答题（本题满分60分，每小题20分）‎ 1、 已知点A(0,2)和抛物线y=x2+4上两点B、C使得AB⊥BC，求点C的纵坐标的取值范围。‎ 解：设B点坐标为B(y12-4,y1)，C点坐标为C(y2-4,y)‎ ‎ 显然y12-4≠0，故 …………5分 ‎ ∵AB⊥BC ‎ ∴KBC= -(y1+2)‎ ‎ ∴‎ ‎ (2+y1)(y+y1)+1=0‎ ‎ y12+(2+y)y1+(2y+1)=0 …………10分 ‎ ∵y1∈R ‎ ∴⊿≥0y≤0或y≥4 …………15分 ‎ ∴当y=0时，点B的坐标为(-3，-1)；当y=4时，点B的坐标为(5，-3)，均满足题意。‎ ‎ 故点C的纵坐标的取值范围为(-∞,0]∪[4,+∞)‎ 2、 如图，有一列曲线P0, P1, P2, ……，已知P0所围成的图形是面积为1的等边三角形，Pk+1是对Pk进行如下操作得到的：将Pk的每条边三等分，以每边中间部分的线段为边，向外作等边三角形，再将中间部分的线段去掉(k=0,1,2,3,…)，记Sn为曲线Pk所围成图形面积。‎ ‎①求数列{Sn}的通项公式；②求。‎ P0‎ P1‎ P2‎ 解：①对P0进行操作，容易看出P0的每条边变成P1的4条边，故P1的边数为3×4；同样，对P1进行操作，P1的每条边变成P2的4条边，故P2的边数为3×42，从而不难得到Pn的边数为3×4n …………5分 ‎ 已知P0的面积为S0=1，比较P1与P0，容易看出P1在P0‎ 的每条边上增加了一个小等边三角形，其面积为，而P0有3条边，故S1=S0+3×=1+‎ ‎ 再比较P2与P1，容易看出P2在P1的每条边上增加了一个小等边三角形，其面积为×，而P1有3×4条边，故S2=S1+3×4×=1++‎ ‎ 类似地有：S3=S2+3×42×=1+++ …………5分 ‎ ∴Sn=‎ ‎ =1+‎ ‎ = (※) …………10分 ‎ 下面用数学归纳法证明(※)式 ‎ 当n=1时，由上面已知(※)式成立，‎ ‎ 假设当n=k时，有Sk=‎ ‎ 当n=k+1时，易知第k+1次操作后，比较Pk+1与Pk，Pk+1在Pk的每条边上增加了一个小等边三角形，其面积为，而Pk有3×4k条边。故 Sk+1=Sk+3×4k×=‎ ‎ 综上所述，对任何n∈N，(※)式成立。‎ ‎ ②‎ 1、 设二次函数f(x)=ax2+bx+c (a,b,c∈R,a≠0)满足条件：‎ ① 当x∈R时，f(x-4)=f(2-x)，且f(x)≥x；‎ ② 当x∈(0,2)时，f(x)≤‎ ③ f(x)在R上的最小值为0。‎ 求最大值m(m>1)，使得存在t∈R，只要x∈[1,m]，就有f(x+t)≤x 解：∵f(x-4)=f(2-x)‎ ‎ ∴函数的图象关于x= -1对称 ‎ ∴ b=2a 由③知当x= -1时,y=0，即a-b+c=0‎ 由①得 f(1)≥1，由②得 f(1)≤1‎ ‎∴f(1)=1，即工+了+以=1，又a-b+c=0‎ ‎∴a= b= c=‎ ‎∴f(x)= …………5分 假设存在t∈R，只要x∈[1,m]，就有f(x+t)≤x 取x=1时，有f(t+1)≤1(t+1)2+(t+1)+≤1-4≤t≤0‎ 对固定的t∈[-4,0]，取x=m，有 f(t +m)≤m ‎(t+m)2+(t+m)+≤m m2-2(1-t)m+(t2+2t+1)≤0‎ ‎≤m≤ …………10分 ‎ ∴m≤≤=9 …………15分 当t= -4时，对任意的x∈[1,9]，恒有 f(x-4)-x=(x2-10x+9)=(x-1)(x-9)≤0‎ ‎∴m的最大值为9。 …………20分 另解：∵f(x-4)=f(2-x)‎ ‎ ∴函数的图象关于x= -1对称 ‎ ∴ b=2a 由③知当x= -1时,y=0，即a-b+c=0‎ 由①得 f(1)≥1，由②得 f(1)≤1‎ ‎∴f(1)=1，即工+了+以=1，又a-b+c=0‎ ‎∴a= b= c=‎ ‎∴f(x)==(x+1)2 …………5分 ‎ 由f(x+t)=(x+t+1)2≤x 在x∈[1,m]上恒成立 ‎ ∴4[f(x+t)-x]=x2+2(t-1)x+(t+1)2≤0当x∈[1,m]时，恒成立 ‎ 令 x=1有t2+4t≤0-4≤t≤0‎ 令x=m有t2+2(m+1)t+(m-1)2≤0当t∈[-4,0]时，恒有解 …………10分 令t= -4得，m2-10m+9≤01≤m≤9 …………15分 即当t= -4时，任取x∈[1,9]恒有 f(x-4)-x=(x2-10x+9)=(x-1)(x-9)≤0‎ ‎∴ mmin=9 …………20分 ‎ ‎