2013年高考数学（理科）真题分类汇编N单元 选修4系列

2013年高考数学（理科）真题分类汇编N单元 选修4系列

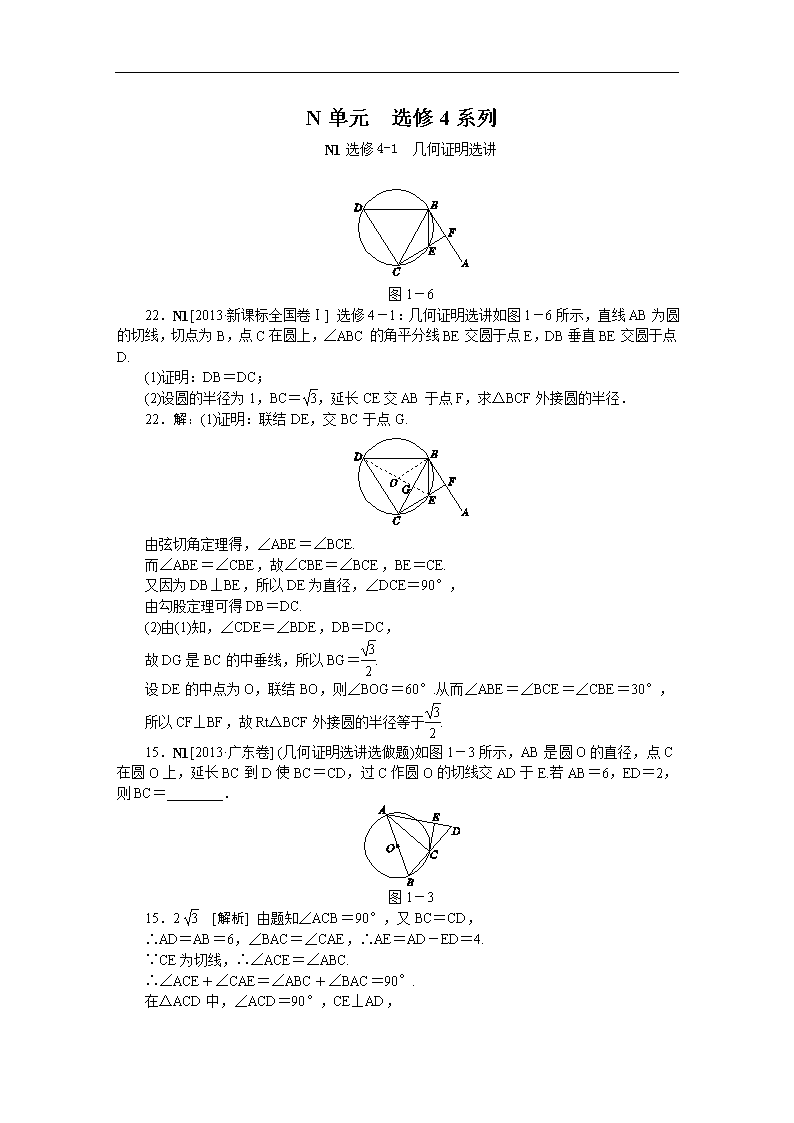
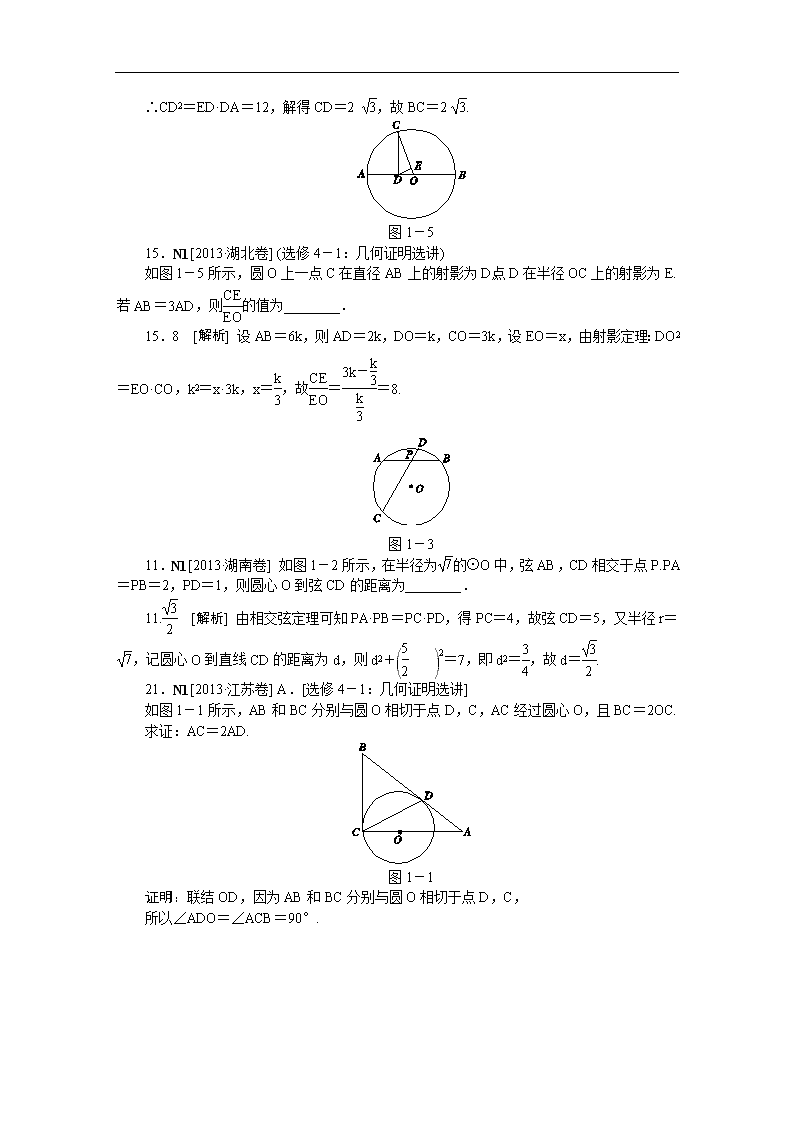
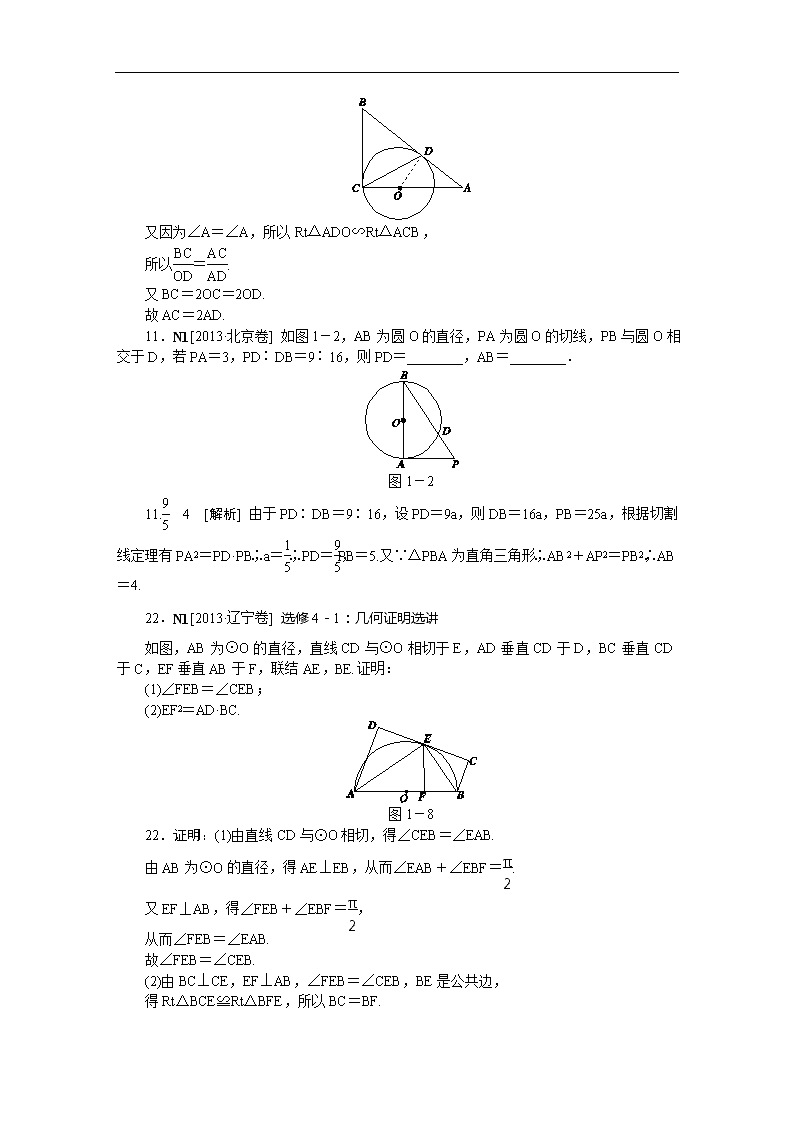
N单元 选修4系列 N1选修4-1 几何证明选讲　　　　　　　　　　　　　　　　　　　　‎ 图1－6‎ ‎22．N1[2013·新课标全国卷Ⅰ] 选修4－1：几何证明选讲如图1－6所示，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.‎ ‎(1)证明：DB＝DC；‎ ‎(2)设圆的半径为1，BC＝，延长CE交AB于点F，求△BCF外接圆的半径．‎ ‎22．解：(1)证明：联结DE，交BC于点G.‎ 由弦切角定理得，∠ABE＝∠BCE.‎ 而∠ABE＝∠CBE，故∠CBE＝∠BCE，BE＝CE.‎ 又因为DB⊥BE，所以DE为直径，∠DCE＝90°，‎ 由勾股定理可得DB＝DC.‎ ‎(2)由(1)知，∠CDE＝∠BDE，DB＝DC，‎ 故DG是BC的中垂线，所以BG＝.‎ 设DE的中点为O，联结BO，则∠BOG＝60°.从而∠ABE＝∠BCE＝∠CBE＝30°，‎ 所以CF⊥BF，故Rt△BCF外接圆的半径等于.‎ ‎15．N1[2013·广东卷] (几何证明选讲选做题)如图1－3所示，AB是圆O的直径，点C在圆O上，延长BC到D使BC＝CD，过C作圆O的切线交AD于E.若AB＝6，ED＝2，则BC＝________．‎ 图1－3‎ ‎15．2 　[解析] 由题知∠ACB＝90°，又BC＝CD，‎ ‎∴AD＝AB＝6，∠BAC＝∠CAE，∴AE＝AD－ED＝4.‎ ‎∵CE为切线，∴∠ACE＝∠ABC.‎ ‎∴∠ACE＋∠CAE＝∠ABC＋∠BAC＝90°.‎ 在△ACD中，∠ACD＝90°，CE⊥AD，‎ ‎∴CD2＝ED·DA＝12，解得CD＝2 ，故BC＝2 .‎ 图1－5‎ ‎15．N1[2013·湖北卷] (选修4－1：几何证明选讲)‎ 如图1－5所示，圆O上一点C在直径AB上的射影为D，点D在半径OC上的射影为E.若AB＝3AD，则的值为________．‎ ‎15．8　[解析] 设AB＝6k，则AD＝2k，DO＝k，CO＝3k，设EO＝x，由射影定理：DO2＝EO·CO，k2＝x·3k，x＝，故＝＝8.‎ 图1－3‎ ‎11．N1[2013·湖南卷] 如图1－2所示，在半径为的⊙O中，弦AB，CD相交于点P.PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．‎ ‎11.　[解析] 由相交弦定理可知PA·PB＝PC·PD，得PC＝4，故弦CD＝5，又半径r＝，记圆心O到直线CD的距离为d，则d2＋＝7，即d2＝，故d＝.‎ ‎21．N1[2013·江苏卷] A．[选修4－1：几何证明选讲]‎ 如图1－1所示，AB和BC分别与圆O相切于点D，C，AC经过圆心O，且BC＝2OC.‎ 求证：AC＝2AD.‎ 图1－1‎ 证明：联结OD，因为AB和BC分别与圆O相切于点D，C，‎ 所以∠ADO＝∠ACB＝90°.‎ 又因为∠A＝∠A，所以Rt△ADO∽Rt△ACB，‎ 所以＝.‎ 又BC＝2OC＝2OD.‎ 故AC＝2AD.‎ ‎11．N1[2013·北京卷] 如图1－2，AB为圆O的直径，PA为圆O的切线，PB与圆O相交于D，若PA＝3，PD∶DB＝9∶16，则PD＝________，AB＝________．‎ 图1－2‎ ‎11.　4　[解析] 由于PD∶DB＝9∶16，设PD＝9a，则DB＝16a，PB＝25a，根据切割线定理有PA2＝PD·PB，∴a＝，∴PD＝，PB＝5.又∵△PBA为直角三角形，∴AB2＋AP2＝PB2，∴AB＝4.‎ ‎22．N1[2013·辽宁卷] 选修4－1：几何证明选讲 如图，AB为⊙O的直径，直线CD与⊙O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直AB于F，联结AE，BE.证明：‎ ‎(1)∠FEB＝∠CEB；‎ ‎(2)EF2＝AD·BC.‎ 图1－8‎ ‎22．证明：(1)由直线CD与⊙O相切，得∠CEB＝∠EAB.‎ 由AB为⊙O的直径，得AE⊥EB，从而∠EAB＋∠EBF＝.‎ 又EF⊥AB，得∠FEB＋∠EBF＝，‎ 从而∠FEB＝∠EAB.‎ 故∠FEB＝∠CEB.‎ ‎(2)由BC⊥CE，EF⊥AB，∠FEB＝∠CEB，BE是公共边，‎ 得Rt△BCE≌Rt△BFE，所以BC＝BF.‎ 类似可证，Rt△ADE≌Rt△AFE，得AD＝AF.‎ 又在Rt△AEB中，EF⊥AB，故EF2＝AF·BF，‎ 所以EF2＝AD·BC.‎ N1[2013·陕西卷] ‎ B．(几何证明选做题)如图1－4，弦AB与CD相交于⊙O内一点E，过E作BC的平行线与AD的延长线相交于点P，已知PD＝2DA＝2，则PE＝________.‎ 图1－4‎ 　[解析] 利用已知可得，∠BCE＝∠PED＝∠BAP，可得△PDE∽△PEA，可得＝，而PD＝2DA＝2，则PA＝3，则PE2＝PA·PD＝6，PE＝.‎ ‎15．C8，E8，N1[2013·四川卷] 设P1，P2，…，Pn为平面α内的n个点，在平面α内的所有点中，若点P到P1，P2，…，Pn点的距离之和最小，则称点P为P1，P2，…，Pn点的一个“中位点”．例如，线段AB上的任意点都是端点A，B的中位点．则有下列命题：‎ ‎①若A，B，C三个点共线，C在线段AB上，则C是A，B，C的中位点；‎ ‎②直角三角形斜边的中点是该直角三角形三个顶点的中位点；‎ ‎③若四个点A，B，C，D共线，则它们的中位点存在且唯一；‎ ‎④梯形对角线的交点是该梯形四个顶点的唯一中位点．‎ 其中的真命题是________．(写出所有真命题的序号)‎ ‎15．①④　[解析] 对于①，如果中位点不在直线AB上，由三角形两边之和大于第三边可知与题意矛盾．而当中位点在直线AB上时，如果不与C重合，则|PA|＋|PB|＋|PC|＞|PA|＋|PB|也不符合题意，故C为唯一的中位点，①正确；‎ 对于②，我们取斜边长为4的等腰直角三角形，此时，斜边中点到三个顶点的距离均为2，和为6；而我们取斜边上中线的中点，该点到直角顶点的距离为1，到两底角顶点的距离均为，显然2 ＋1＜6，故该直角三角形的斜边中点不是中位点，②错误；‎ 对于③，当A，B，C，D四点共线时，不妨设他们的顺序就是A，B，C，D，则当点P在B，C之间运动时，点P到A，B，C，D四点的距离之和相等且最小，即这个时候的中位点有无穷多个，③错误；‎ 对于④，同样根据三角形两边之和大于第三边的性质，如果中位点不在对角线的交点上，则距离之和肯定不是最小的，④正确．‎ ‎13．N1[2013·天津卷] 如图1－2所示，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC.过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F，若AB＝AC，AE＝6，BD＝5，则线段CF的长为________．‎ 图1－2‎ ‎13.　[解析] 由切割线定理可得EA2＝EB·ED，有EB＝4，ED＝9.‎ 因为AB＝AC，所以∠ABC＝∠C＝∠ADB，‎ 由弦切角定理可得∠EAB＝∠ADB，所以∠EAB＝∠ABC，故AE∥BC.又BD∥AC，‎ 所以四边形AEBC是平行四边形，可得BC＝AE＝6，又由平行线分线段成比例定理可得＝，因为AE＝6，所以BF＝，故CF＝BC－BF＝.‎ ‎22．N1[2013·新课标全国卷Ⅱ] 选修4－1：几何证明选讲：‎ 如图1－5，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC·AE＝DC·AF，B，E，F，C四点共圆．‎ ‎(1)证明：CA是△ABC外接圆的直径；‎ ‎(2)若DB＝BE＝EA，求过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值．‎ 图1－5‎ ‎22．解：(1)证明：因为CD为△ABC外接圆的切线，所以∠DCB＝∠A，由题设知＝，‎ 故△CDB∽△AEF，所以∠DBC＝∠EFA.‎ 因为B，E，F，C四点共圆，所以∠CFE＝∠DBC，故∠EFA＝∠CFE＝90°.所以∠CBA＝90°，因此CA是△ABC外接圆的直径．‎ ‎(2)联结CE，因为∠CBE＝90°，所以过B，E，F，C四点的圆的直径为CE，由DB＝BE，有CE＝DC，又BC2＝DB·BA＝2DB2，所以CA2＝4DB2＋BC2＝6DB2.‎ 而DC2＝DB·DA＝3DB2，故过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值为.‎ ‎1－6‎ ‎14．N1[2013·重庆卷] 如图1－6所示，在△ABC中，∠C＝90°，∠A＝60°，AB＝20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，则DE的长为________．‎ ‎14．5　[解析] 联结CE.由弦切角定理知∠BCD＝∠A＝60°，所以在Rt△BCD中，∠CBD＝30°.又在Rt△ABC中，∠ABC＝30°，AC＝AB＝10，所以CE＝AC＝10.在Rt△‎ CDE中，∠DCE＝30°，故DE＝CE＝5.‎ N2　选修4-2 矩阵　　　　　　　　　　　　　　　　　　　‎ ‎21．[2013·福建卷] N2(Ⅰ)选修4－2：矩阵与变换 已知直线l：ax＋y＝1在矩阵A＝)对应的变换作用下变为直线l′：x＋by＝1.‎ ‎(1)求实数a，b的值；‎ ‎(2)若点P(x0，y0)在直线l上，且A)＝)，求点P的坐标．‎ ‎(Ⅰ)解：(1)设直线l：ax＋y＝1上任意点M(x，y)在矩阵A对应的变换作用下的像是M′(x′，y′)．‎ 由)＝)))＝)，得 又点M′(x′，y′)在l′上，所以x′＋by′＝1，‎ 即x＋(b＋2)y＝1.‎ 依题意得解得 ‎(2)由A)＝)，得解得y0＝0.‎ 又点P(x0，y0)在直线l上，所以x0＝1.‎ 故点P的坐标为(1，0)．‎ N2[2013·江苏卷] ‎ B．[选修4－2：矩阵与变换]‎ 已知矩阵A＝－1,0)　0,2)，B＝1,0)　2,6)，求矩阵A－1B.‎ 解：设矩阵A的逆矩阵为a,c)　b,d)，‎ 则－1,0)　0,2)a,c)　b,d)＝1,0)　0,1)．‎ 即－a,2c)　－b,2d)＝1,0)　0,1)，‎ 故a＝－1，b＝0，c＝0，d＝，‎ 从而A的逆矩阵为A－1＝　0,)))．‎ 所以A－1B＝　0,)))1,0)　2,6)＝－1,0)　－2,3)．‎ ‎2．N2，N3[2013·浙江卷] 已知a∈R“矩阵与变换和坐标系与参数方程”模块 ‎(1)以极坐标系Ox的极点O为原点，极轴Ox为x轴正半轴建立平面直角坐标系xOy，并在两种坐标系中取相同的长度单位．把极坐标方程cos θ＋ρ2sin θ＝1化成直角坐标方程．‎ ‎(2)在直角坐标系xOy中，曲线C：(θ为参数)，过点P(2，1)的直线与曲线C交于A，B两点．若|PA|·|PB|＝，求|AB|的值．‎ ‎2．解：(1)极坐标方程两边同乘以ρ得ρcos θ＋ρ3sin θ＝ρ.‎ 又在直角坐标系下，ρcos θ＝x，ρsin θ＝y，ρ2＝x2＋y2，‎ 故化成直角坐标方程为x＋y(x2＋y2)＝.‎ 又(0，0)满足原极坐标方程．‎ 故所求的直角坐标方程为x＋y(x2＋y2)＝.‎ ‎(2)由题意，曲线C的直角坐标方程为x2＋2y2＝2.‎ 设过点P(2，1)，倾斜角为α的直线的参数方程为 (t为参数)．‎ 及点A，B对应的参数分别为t1，t2.‎ 将直线的参数方程代入x2＋2y2＝2得 ‎(2＋tcos α)2＋2(1＋tsin α)2－2＝0.‎ 即(1＋sin2α)t2＋4(sin α＋cos α)t＋4＝0.‎ 则Δ＝16(2sin αcos α－sin2 α)>0，且t1＋t2＝－，t1t2＝，‎ 由|PA|·|PB|＝得|t1t2|＝＝.‎ 故sin2 α＝.又由Δ>0得0b>0)．在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)‎ 中，直线l与圆O的极坐标方程分别为ρsinθ＋＝m(m为非零常数)与ρ＝b.若直线l经过椭圆C的焦点，且与圆O相切，则椭圆C的离心率为________．‎ ‎16.　[解析] 直线l的直角坐标方程为x＋y－m＝0，圆O的直角坐标方程为x2＋y2＝b2，由直线与圆相切得：m2＝2b2.又椭圆C的一般方程为＋＝1，直线过椭圆焦点，故m＝c，所以c2＝2b2e＝＝.‎ ‎9．N3[2013·湖南卷] 在平面直角坐标系xOy中，若直线l：(t为参数)过椭圆C：(φ为参数)的右顶点，则常数a的值为________．‎ ‎9．3　[解析] 将参数方程化为普通方程可得，直线l：即y＝x－a，椭圆C：即＋＝1，可知其右顶点为(3，0)，代入直线方程可得a＝3.‎ N3[2013·江苏卷] ‎ C．[选修4－4：坐标系与参数方程]‎ 在平面直角坐标系xOy中，直线l的参数方程为(t为参数)，曲线C的参数方程为(θ为参数)，试求直线l和曲线C的普通方程，并求出它们的公共点的坐标．‎ 解：因为直线l的参数方程为(t为参数)，由x＝t＋1得t＝x－1，代入y＝2t，得到直线l的普通方程为2x－y－2＝0.‎ 同理得到曲线C的普通方程为y2＝2x.‎ 联立方程组解得公共点的坐标为(2，2)，，－1.‎ ‎15．[2013·江西卷] N3(1)(坐标系与参数方程选做题)设曲线C的参数方程为(t为参数)，若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为________．‎ N4[2013·江西卷] (2)(不等式选做题)在实数范围内，不等式||x－2|－1|≤1的解集为__________________．‎ ‎15．(1)ρcos2θ－sin θ＝0　(2) ‎[解析] (1)曲线方程为y＝x2，将y＝ρsin θ，x＝ρcos θ代入得ρcos2θ－sin θ＝0.‎ ‎(2)－1≤|x－2|－1≤10≤|x－2|≤2－2≤x－2≤2，得0≤x≤4.‎ ‎23．N3[2013·辽宁卷] 选修4－4：坐标系与参数方程 在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系．圆C1，直线C2的极坐标方程分别为ρ＝4sin θ，ρcos＝2 .‎ ‎(1)求C1与C2交点的极坐标；‎ ‎(2)设P为C1的圆心，Q为C1与C2交点连线的中点．已知直线PQ的参数方程为(t∈R为参数)，求a，b的值．‎ ‎23．解：(1)圆C1的直角坐标方程为x2＋(y－2)2＝4，‎ 直线C2的直角坐标方程为x＋y－4＝0.‎ 解得 所以C1与C2交点的极坐标为，.‎ 注：极坐标系下点的表示不唯一．‎ ‎(2)由(1)可得，P点与Q点的直角坐标分别为(0，2)，(1，3)，‎ 故直线PQ的直角坐标方程为x－y＋2＝0.‎ 由参数方程可得y＝x－＋1，‎ 所以解得a＝－1，b＝2.‎ C．N3[2013·陕西卷] ‎ ‎(坐标系与参数方程选做题)如图1－5，以过原点的直线的倾斜角θ为参数，则圆x2＋y2－x＝0的参数方程为________．‎ 图1－5‎ (θ为参数)　[解析] 设P(x，y)，则随着θ取值变化，P可以表示圆上任意一点，由所给的曲线方程x2＋y2－x＝0x－2＋y2＝，表示以，0为圆心，半径为的圆，可得弦OP＝1×cosθ，所以可得故已知圆的参数方程为(θ为参数)．‎ ‎11．N3[2013·天津卷] 已知圆的极坐标方程为ρ＝4cos θ，圆心为C，点P的极坐标为4，，则|CP|＝________.‎ ‎11．2 　[解析] ∵圆的极坐标方程为ρ＝4cos θ，∴圆心C的直角坐标为(2，0)．∵P点极坐标，∴化为直角坐标为(2，2)，∴|CP|＝＝2 .‎ ‎23．N3[2013·新课标全国卷Ⅱ] 选修4—4：坐标系与参数方程 已知动点P，Q都在曲线C：(t为参数)上，对应参数分别为t＝α与t＝2α(0<α<2π)，M为PQ的中点．‎ ‎(1)求M的轨迹的参数方程；‎ ‎(2)将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．‎ ‎23．解：(1)依题意有P(2cos α，2sin α)，Q(2cos 2α，2sin 2α)，因此M(cos α＋cos 2α，sin α＋sin 2α)．‎ M的轨迹的参数方程为 ‎(α为参数，0<α<2π)．‎ ‎(2)M点到坐标原点的距离 d＝＝(0<α<2π)．‎ 当α＝π时，d＝0，故M的轨迹过坐标原点．‎ ‎2．N2，N3[2013·浙江卷] 已知a∈R“矩阵与变换和坐标系与参数方程”模块 ‎(1)以极坐标系Ox的极点O为原点，极轴Ox为x轴正半轴建立平面直角坐标系xOy，并在两种坐标系中取相同的长度单位．把极坐标方程cos θ＋ρ2sin θ＝1化成直角坐标方程．‎ ‎(2)在直角坐标系xOy中，曲线C：(θ为参数)，过点P(2，1)的直线与曲线C交于A，B两点．若|PA|·|PB|＝，求|AB|的值．‎ ‎2．解：(1)极坐标方程两边同乘以ρ得ρcos θ＋ρ3sin θ＝ρ.‎ 又在直角坐标系下，ρcos θ＝x，ρsin θ＝y，ρ2＝x2＋y2，‎ 故化成直角坐标方程为x＋y(x2＋y2)＝.‎ 又(0，0)满足原极坐标方程．‎ 故所求的直角坐标方程为x＋y(x2＋y2)＝.‎ ‎(2)由题意，曲线C的直角坐标方程为x2＋2y2＝2.‎ 设过点P(2，1)，倾斜角为α的直线的参数方程为 (t为参数)．‎ 及点A，B对应的参数分别为t1，t2.‎ 将直线的参数方程代入x2＋2y2＝2得 ‎(2＋tcos α)2＋2(1＋tsin α)2－2＝0.‎ 即(1＋sin2α)t2＋4(sin α＋cos α)t＋4＝0.‎ 则Δ＝16(2sin αcos α－sin2 α)>0，且t1＋t2＝－，t1t2＝，‎ 由|PA|·|PB|＝得|t1t2|＝＝.‎ 故sin2 α＝.又由Δ>0得00，求证：2a3－b3≥2ab2－a2b.‎ 证明：2a3－b3－(2ab2－a2b)＝2a(a2－b2)＋b(a2－b2)＝(a2－b2)(2a＋b)＝(a－b)(a＋b)(2a＋b)．‎ 因为a≥b>0，所以a－b≥0，a＋b>0，2a＋b>0.‎ 从而(a－b)(a＋b)(2a＋b)≥0，即2a3－b3≥2ab2－a2b.24.N4[2013·辽宁卷] 选修4－5：不等式选讲 已知函数f(x)＝|x－a|，其中a>1.‎ ‎(1)当a＝2时，求不等式f(x)≥4－|x－4|的解集；‎ ‎(2)已知关于x的不等式|f(2x＋a)－2f(x)|≤2的解集为，求a的值．‎ ‎24．解：(1)当a＝2时，f(x)＋|x－4|＝ 当x≤2时，由f(x)≥4－|x－4|得－2x＋6≥4，解得x≤1；‎ 当2＜x＜4时，f(x)≥4－|x－4|无解；‎ 当x≥4时，由f(x)≥4－|x－4|得2x－6≥4，解得x≥5；‎ 所以f(x)≥4－|x－4|的解集为{x|x≤1或x≥5}．‎ ‎(2)记h(x)＝f(2x＋a)－2f(x)，则 h(x)＝ 由|h(x)|≤2，解得≤x≤.‎ 又已知|h(x)|≤2的解集为{x|1≤x≤2}，‎ 所以于是a＝3.‎ ‎15．N4[2013·陕西卷] (考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分)‎ A．(不等式选做题)已知a，b，m，n均为正数，且a＋b＝1，mn＝2，则(am＋bn)(bm＋an)的最小值为________．‎ ‎2　[解析] 利用柯西不等式式可得：(am＋bn)(bm＋an)≥(＋)2＝mn(a＋b)2＝2.‎ ‎14．N4[2013·天津卷] 设a＋b＝2，b>0，则当a＝________时，＋取得最小值．‎ ‎14．－2　[解析] ＋＝＋＝＋＋≥＋2 ≥－＋1＝，当且仅当＝时，等号成立．联立a＋b＝2，b>0，a<0.可解得a＝－2.‎ ‎24．N4[2013·新课标全国卷Ⅱ] 选修4－5：不等式选讲 设a，b，c均为正数，且a＋b＋c＝1，证明：‎ ‎(1)ab＋bc＋ca≤；‎ ‎(2)＋＋≥1.‎ ‎24．证明：(1)由a2＋b2≥2ab，b2＋c2≥2bc，c2＋a2≥2ca得 a2＋b2＋c2≥ab＋bc＋ca.‎ 由题设得(a＋b＋c)2＝1，即a2＋b2＋c2＋2ab＋2bc＋2ca＝1.‎ 所以3(ab＋bc＋ca)≤1，即ab＋bc＋ca≤.‎ ‎(2)因为 ＋b≥2a，＋c≥2b，＋a≥2c，‎ 故＋＋＋(a＋b＋c)≥2(a＋b＋c)，即＋＋≥a＋b＋c，又a＋b＋c＝1，‎ 所以＋＋≥1.‎ ‎1．N4[2013·浙江卷] (1)解不等式|x－1|＋|x－4|≥5.‎ ‎(2)求函数y＝|x－1|＋|x－4|＋x2－4x的最小值．‎ ‎1．解：(1)当x<1时，1－x＋4－x≥5，得x≤0，此时x≤0；‎ 当1≤x≤4时，x－1＋4－x≥5，得3≥5，此时x∈；‎ 当x>4时，x－1＋x－4≥5，得x≥5，此时x≥5.‎ 综上所述，原不等式的解集是(－∞，0]∪[5，＋∞)．‎ ‎(2)因为|x－1|＋|x－4|≥|(x－1)－(x－4)|＝3，‎ 当且仅当1≤x≤4时取等号；‎ x2－4x＝(x－2)2－4≥－4，当且仅当x＝2时取等号．‎ 故|x－1|＋|x－4|＋x2－4x≥3－4＝－1，当x＝2时取等号．‎ 所以y＝|x－1|＋|x－4|＋x2－4x的最小值为－1.‎ ‎16．N4[2013·重庆卷] 若关于实数x的不等式|x－5|＋|x＋3|＜a无解，则实数a的取值范围是________．‎ ‎16．(－∞，8]　[解析] 要使不等式无解，则a必须小于或等于|x－5|＋|x＋3|的最小值，而|x－5|＋|x＋3|≥|(x－5)－(x＋3)|＝8，则a≤8，所以实数a的取值范围是(－∞，8]．‎ N5 选修4-7 优选法与试验设计